Содержание
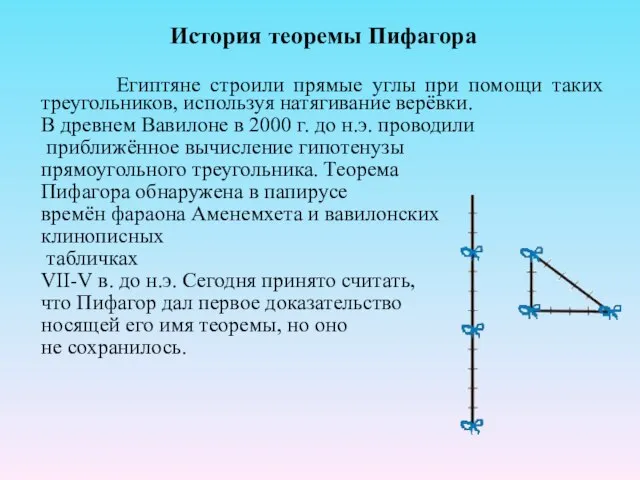
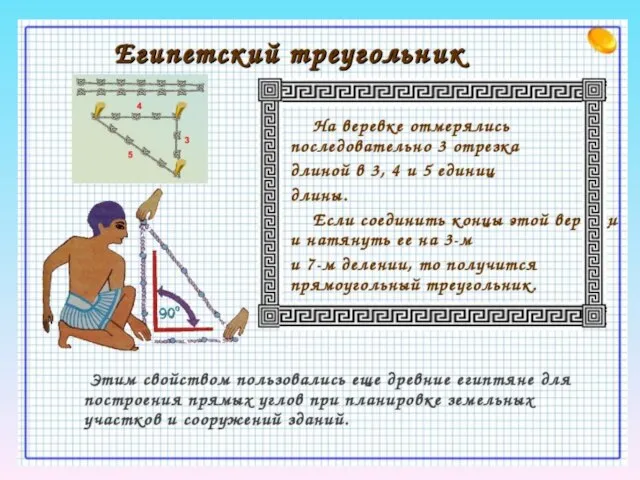
- 2. История теоремы Пифагора Египтяне строили прямые углы при помощи таких треугольников, используя натягивание верёвки. В древнем
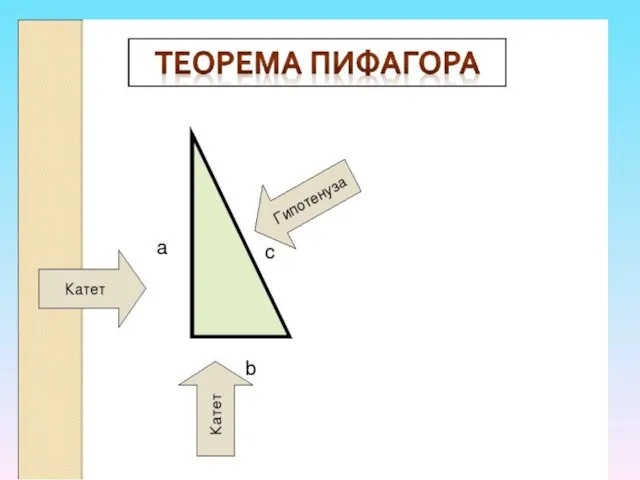
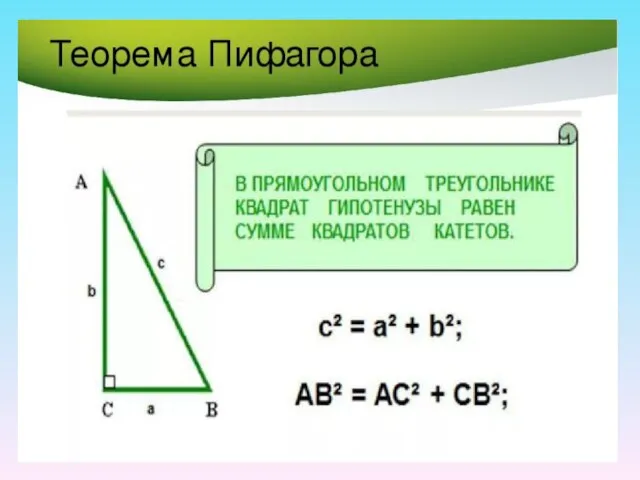
- 7. Доказательство теоремы Пифагора Дано: прямоугольный треугольник с катетами а, b и гипотенузой с Док-ть: Док-во: достроим
- 8. Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его «ослиным мостом» или «бегством убогих»,
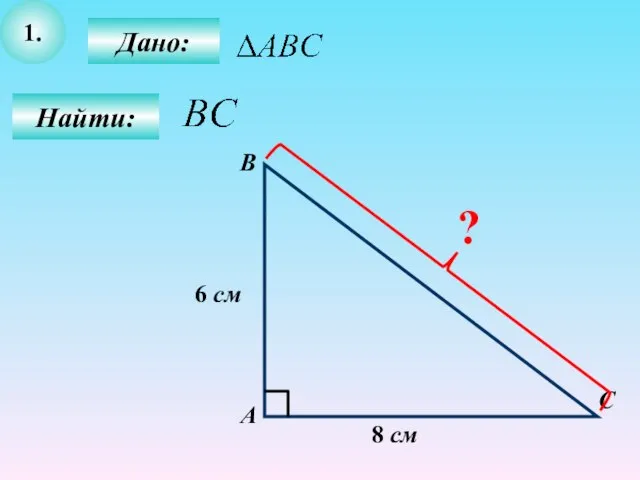
- 10. 1. Найти: С В А Дано: 8 см 6 см ?
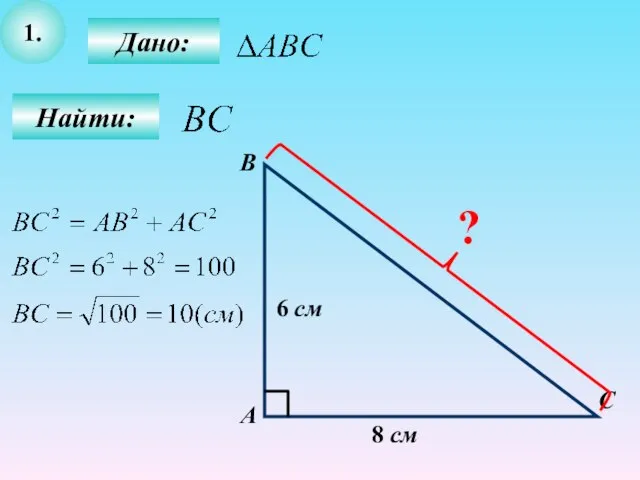
- 11. 1. Найти: С В А Дано: 8 см 6 см ?
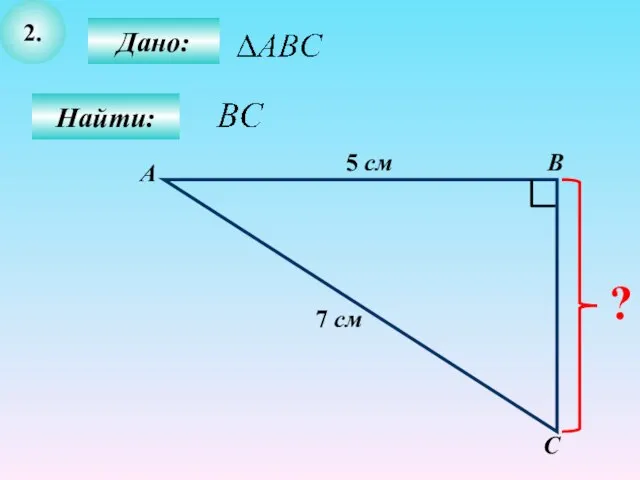
- 12. 2. Дано: С В Найти: А 5 см 7 см ?
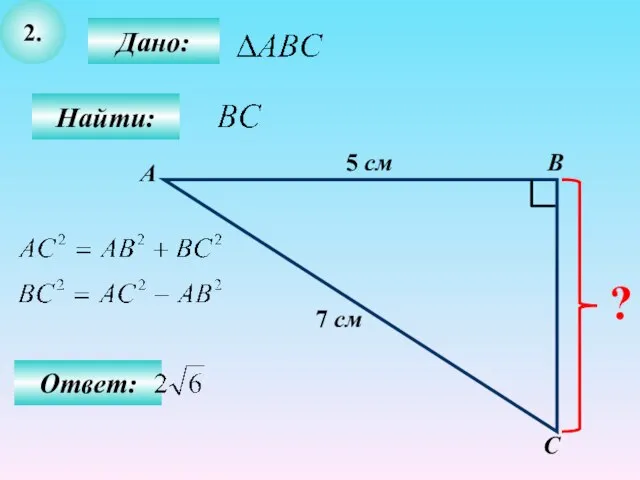
- 13. 2. Дано: С В Найти: А 5 см 7 см ? Ответ:
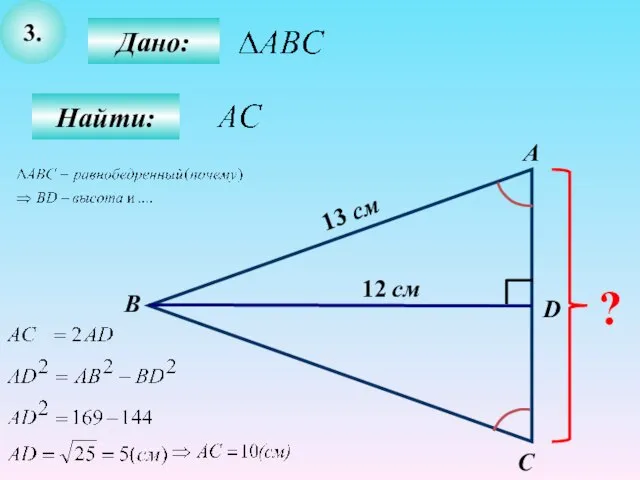
- 14. 3. Дано: Найти: А B C D ? 12 см 13 см
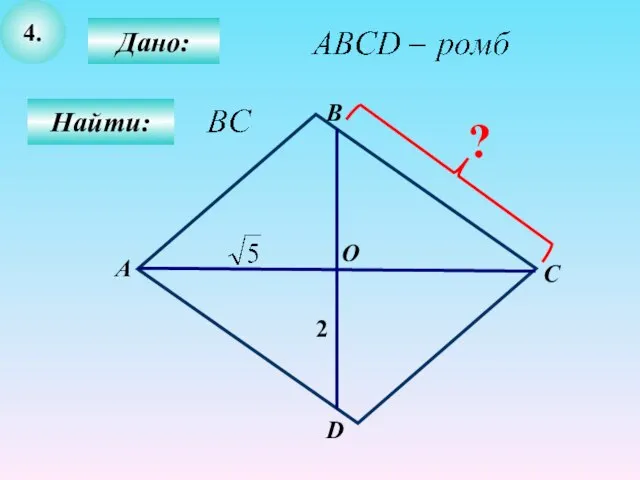
- 15. 4. Дано: Найти: В А С О D 2 ?
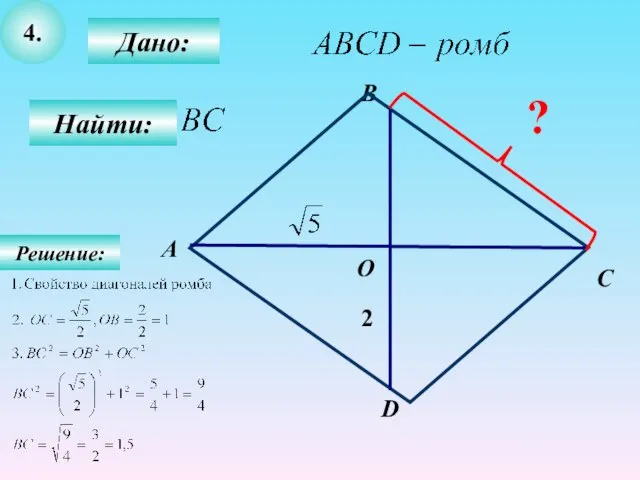
- 16. 4. Дано: Найти: В А С О D 2 ? Решение:
- 18. Скачать презентацию




 Решение неравенств с одной переменной
Решение неравенств с одной переменной Презентация на тему Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы
Презентация на тему Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы  Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2)
Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2) Теория пределов. Лекция 4
Теория пределов. Лекция 4 Разбиение множеств на классы
Разбиение множеств на классы Дифференциальные уравнения
Дифференциальные уравнения Символика. Взаимное расположение точек и прямой
Символика. Взаимное расположение точек и прямой Тема урока: Умножение чисел на сумму
Тема урока: Умножение чисел на сумму Ну, погоди!
Ну, погоди!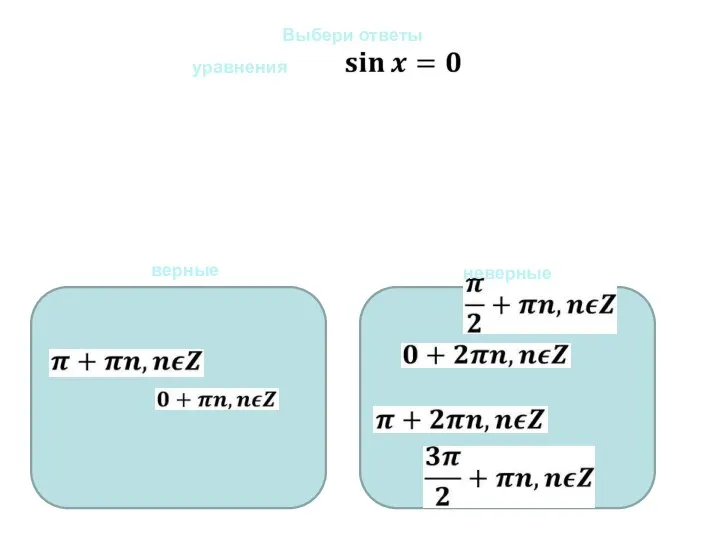 Уравнения sinx=0, cosx=0. Выберите правильный ответ
Уравнения sinx=0, cosx=0. Выберите правильный ответ Задачи, обратные данной
Задачи, обратные данной Презентация на тему Геометрическая прогрессия
Презентация на тему Геометрическая прогрессия  Геометрическая прогрессия
Геометрическая прогрессия Проценты. Примеры цепочкой
Проценты. Примеры цепочкой Презентация на тему Леонтий Филиппович Магницкий
Презентация на тему Леонтий Филиппович Магницкий  Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Степень с рациональным показателем
Степень с рациональным показателем Классификация: общие принципы
Классификация: общие принципы Издательство Легион. Задачи с параметром в ОГЭ
Издательство Легион. Задачи с параметром в ОГЭ Теорема Пифагора. Чертеж к доказательству Пифагора
Теорема Пифагора. Чертеж к доказательству Пифагора Тождественные преобразования рациональных выражений
Тождественные преобразования рациональных выражений Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Понятие математической индукции и ее применение
Понятие математической индукции и ее применение Упрощение выражений. Тест
Упрощение выражений. Тест Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Презентация на тему Нахождение дроби от числа. Нахождение числа
Презентация на тему Нахождение дроби от числа. Нахождение числа  Признаки классификации статистической сводки
Признаки классификации статистической сводки