Теоремы к зачёту

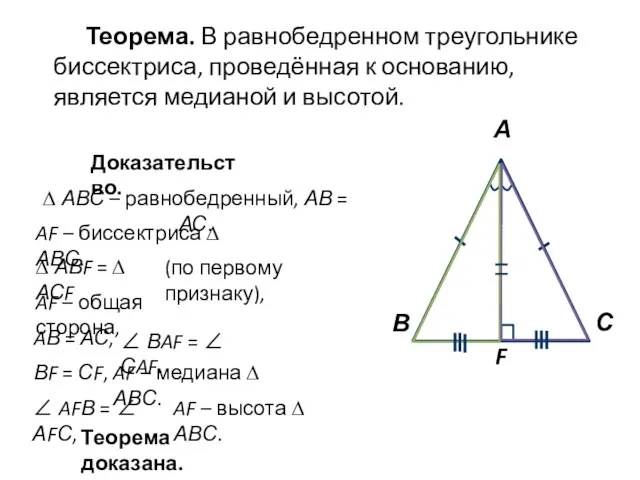
Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство.
AВ = АС,
∠ ВAF = ∠ СAF.
AF – медиана ∆ АВС.
∠ AFВ = ∠ АFС,
AF – высота ∆ АВС.
Теорема доказана.
(по первому признаку),

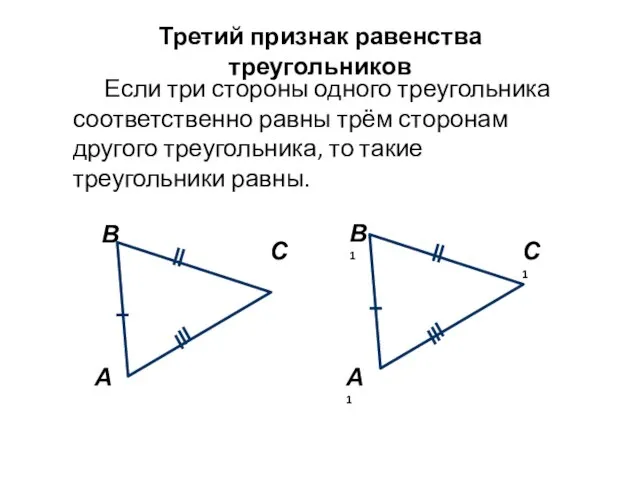
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
А
А1
С1
В1
С
В

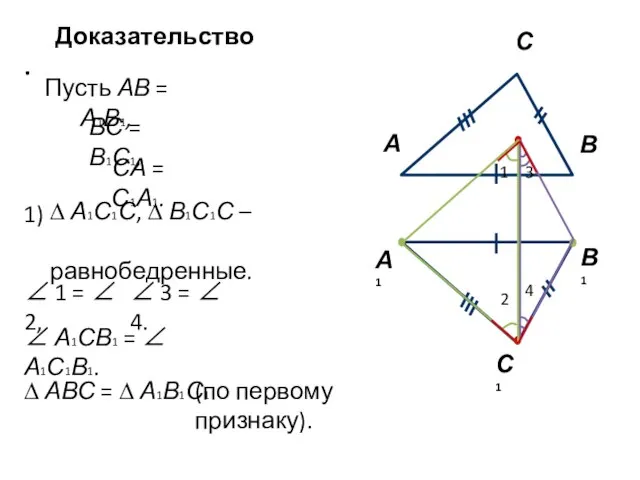
Доказательство.
А1
В1
С1
Пусть АВ = А1В1,
ВС = В1С1,
СА = С1А1.
1)
∆ А1С1С, ∆ В1С1С –
равнобедренные.
∠ 1 = ∠ 2,
∠ 3 = ∠ 4.
∠ А1СВ1 = ∠ А1С1В1.
∆ АВС = ∆ А1В1С1
(по первому признаку).
1
2
3
4

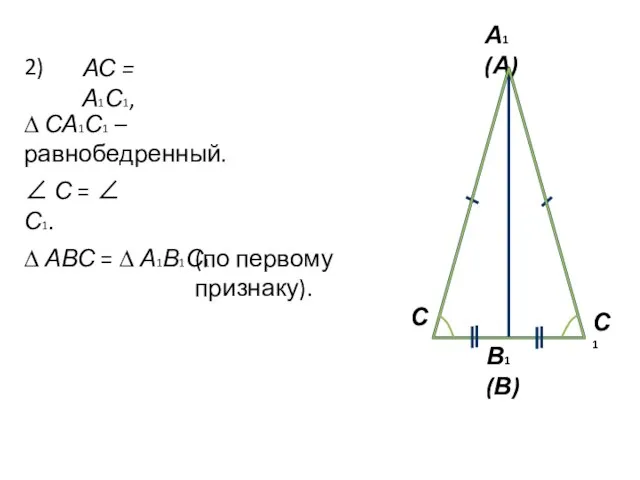
2)
АС = А1С1,
∆ СА1С1 – равнобедренный.
∠ С = ∠ С1.
∆ АВС = ∆ А1В1С1
(по первому признаку).
С
А1 (А)
В1 (В)
С1