лекция №4АиГ

План лекции:
Системы линейных уравнений. Основные понятия.
Матричный метод решения систем линейных уравнений.
Правило Крамера.

Системы линейных уравнений.
Основные понятия.
Системой из m линейных уравнений c n неизвестными называется система вида:
(1)
Здесь переменные
называются неизвестными системы, числа аij, где i = 1, 2,…, m; j = 1, 2,…, n называются коэффициентами системы, а числа
– свободными членами.

Определение. Решением системы называется упорядоченный набор чисел
( ),
который после подстановки в систему (1) превращает все её уравнения в тождества.
Определение. Две системы называются эквивалентными, если решение первой является решением второй и наоборот.
Система называется однородной, если все её свободные члены равны нулю
иначе — неоднородной

Определение. Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной.
Определение. Система, имеющая единственное решение, называется определенной, а имеющая более одного решения – неопределенной.
Однородная система всегда совместна, то есть всегда имеет решение.

Обозначим:
A=
X =
В =

Тогда систему (1) можно записать в виде матричного уравнения:
AX = B. (2)
Это запись называется матричной формой записи системы (1) .
.

Матричный метод решения систем линейных уравнений

Правило Крамера.

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей.
В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

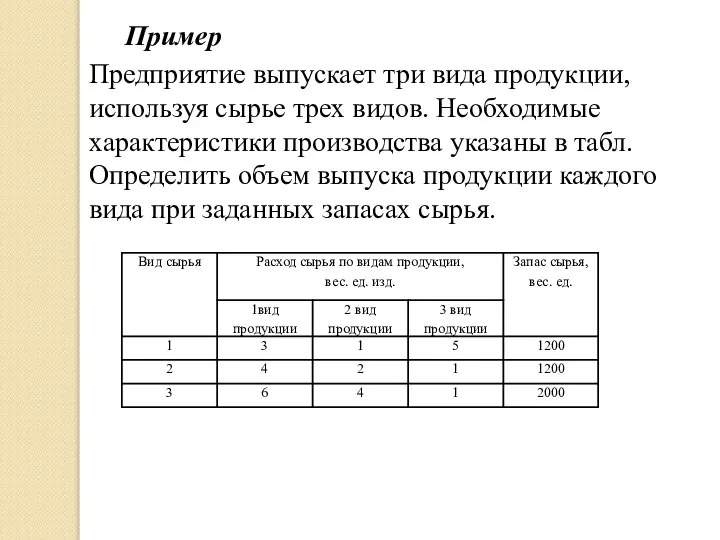
Пример
Предприятие выпускает три вида продукции, используя сырье трех видов. Необходимые характеристики производства указаны в табл. Определить объем выпуска продукции каждого вида при заданных запасах сырья.

Решение. Пусть xi - объем выпуска продукции i-го вида, i =1, 2, 3. При условии полного расхода запасов каждого вида сырья составим балансовые соотношения:

Вычислим определитель матрицы А:
определитель матрицы не равен нулю, следовательно решение существует
2) находим алгебраические дополнения к каждому элементу:

Тогда обратная матрица равна
Находим решение:
Тогда
Ответ: При заданных запасах сырья объемы выпуска продукции по каждому виду составят соответственно
150, 250 и 100 условных единиц

Решить систему уравнений с помощью формул Крамера:

Откуда решение системы:
3) Проверяем подстановкой полученных значений в исходную систему:
Ответ:

Решить систему линейных уравнений методом Крамера:
.

Решение. Находим определитель системы:
Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:
Итак, решение системы - (2; -1; 1).

Решить систему линейных уравнений методом Крамера:
.
Решение:
1) Составим определители, соответствующие исходной системе и каждому неизвестному:
;
;
;

2) Вычислим определитель системы: сложим соответствующие элементы первой и второй строк, затем первой и третьей, получим во втором столбце нули, кроме элемента в первой строке. Найдем определитель разложением по второму столбцу:
Определитель ненулевой, значит, система имеет решение.

Откуда решение системы:

3) Проверяем подстановкой полученных значений в исходную систему:
Ответ:

Контрольные вопросы:
1.Что называется решением системы линейных уравнений?
2.Какие системы называются совместными, а какие – несовместными?
3. Что называется матрицей и расширенной матрицей системы линейных уравнений?
4. В чем состоит матричный способ решения систем линейных уравнений?
5. Напишите формулы Крамера. В каком случае они применимы?