Содержание
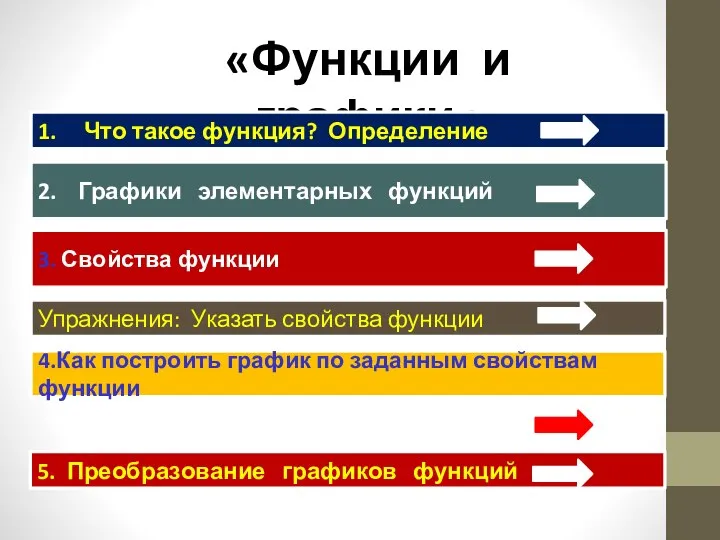
- 2. «Функции и графики» 1. Что такое функция? Определение 2. Графики элементарных функций 3. Свойства функции 5.
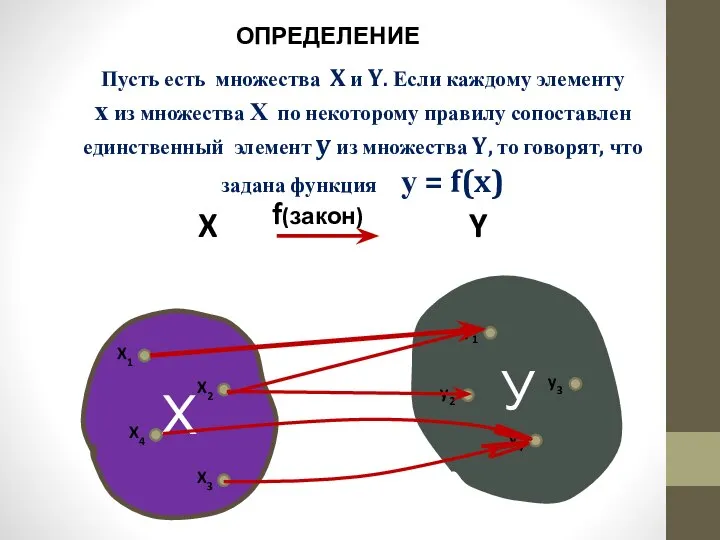
- 3. Пусть есть множества X и Y. Если каждому элементу х из множества Х по некоторому правилу
- 5. 1) Формулой Способы задания функции у = х2 + 2х – 4 у = 3х f(x)
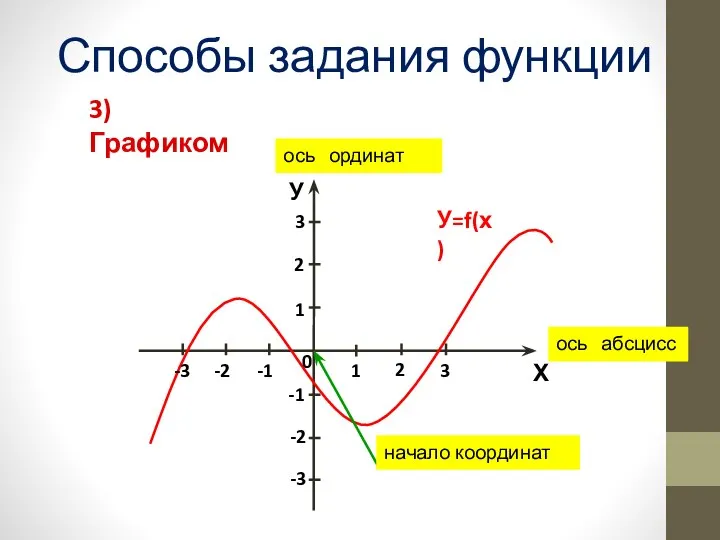
- 6. У=f(х) У Х 0 ось ординат ось абсцисс начало координат Способы задания функции 3) Графиком 1
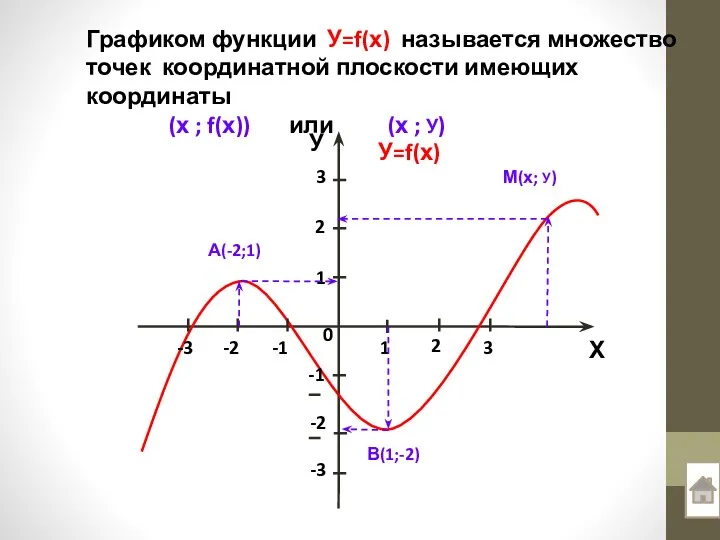
- 7. А(-2;1) В(1;-2) М(х; У) Графиком функции У=f(х) называется множество точек координатной плоскости имеющих координаты (х ;
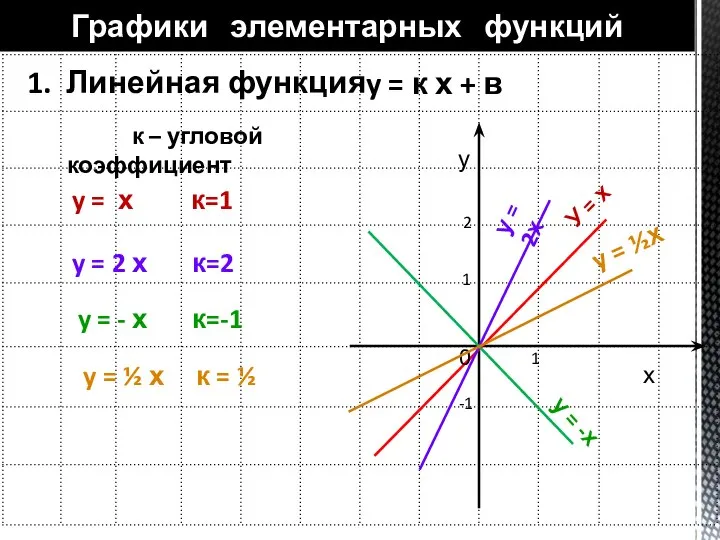
- 8. 1. Линейная функция Графики элементарных функций у х У = х у = 2х у =
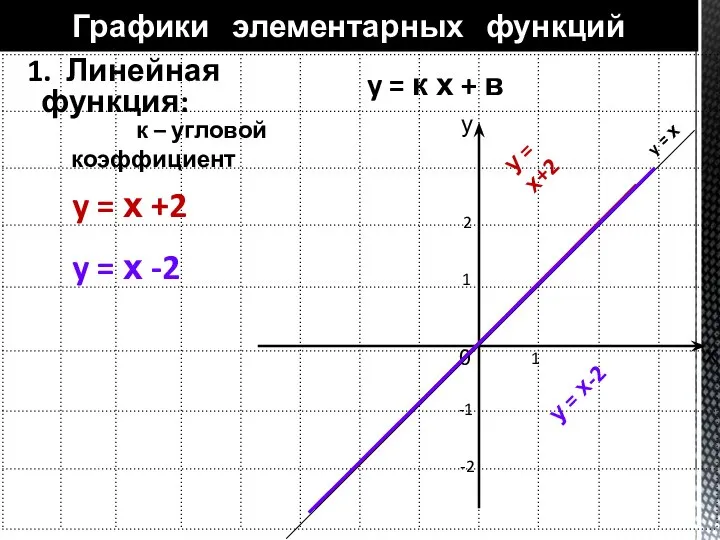
- 9. 1. Линейная функция: Графики элементарных функций у х y = к х + в к –
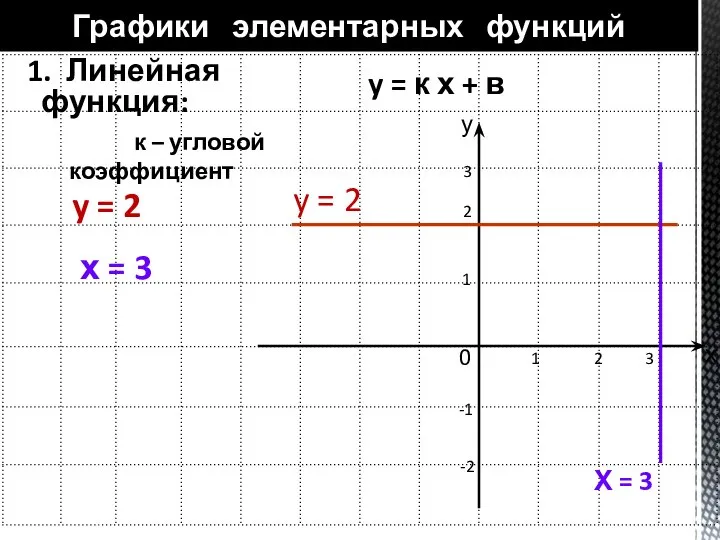
- 10. 1. Линейная функция: Графики элементарных функций у х y = к х + в к –
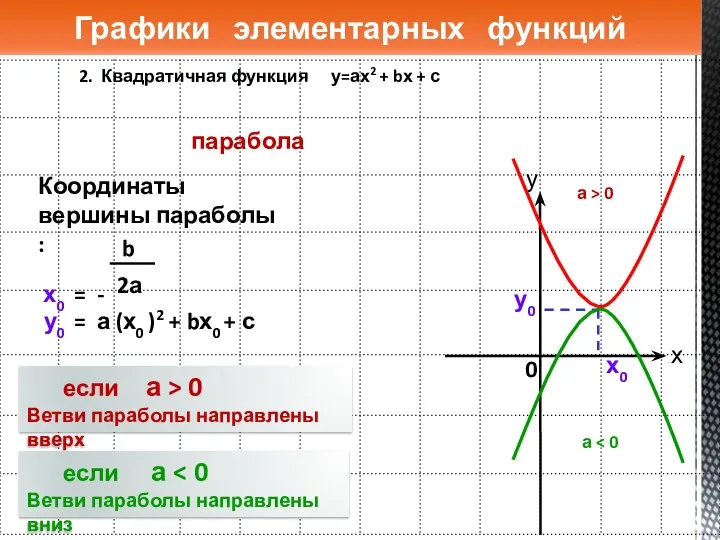
- 11. 2. Квадратичная функция у=ах2 + bх + с Графики элементарных функций 0 х0 у0 парабола если
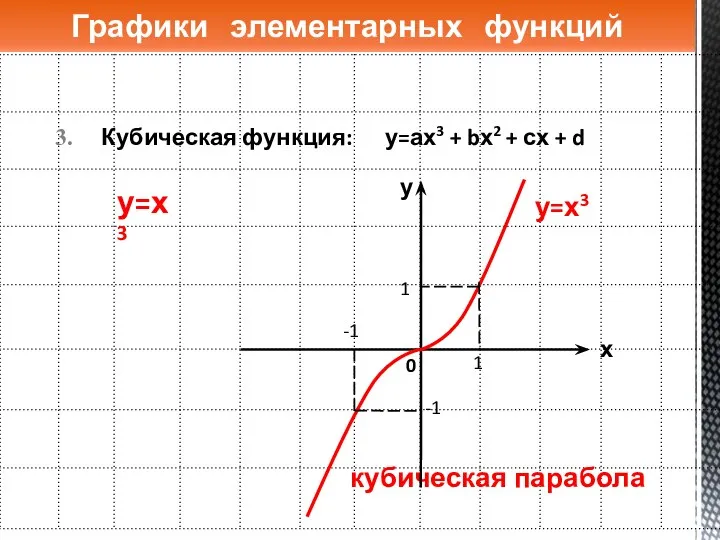
- 12. Кубическая функция: у=ах3 + bх2 + сх + d Графики элементарных функций кубическая парабола 0 у=х3
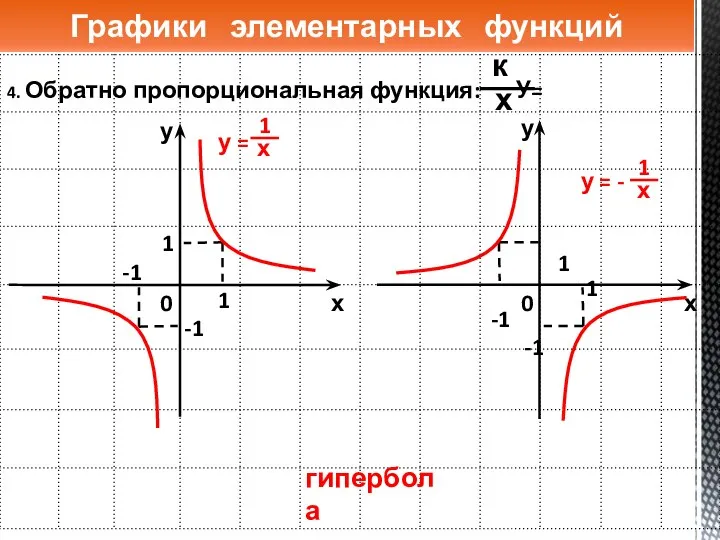
- 13. 4. Обратно пропорциональная функция: У= Графики элементарных функций гипербола 1 -1 1 -1 у = -
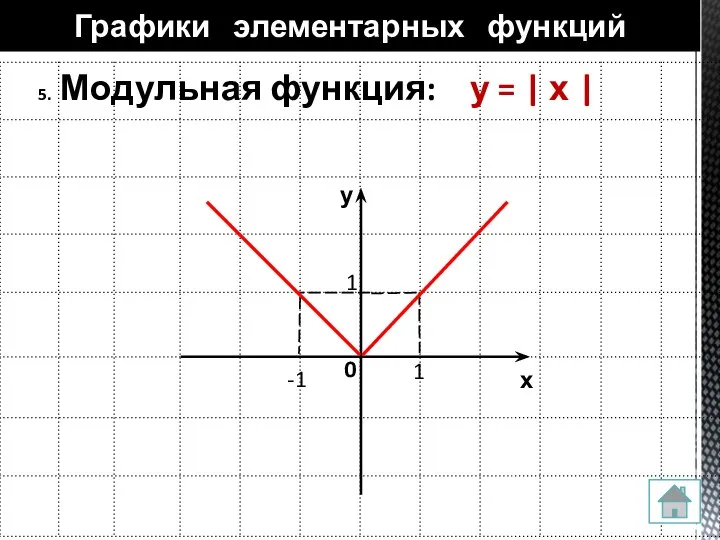
- 14. 5. Модульная функция: у = | х | Графики элементарных функций 0 1 1 -1
- 15. СВОЙСТВА ФУНКЦИЙ
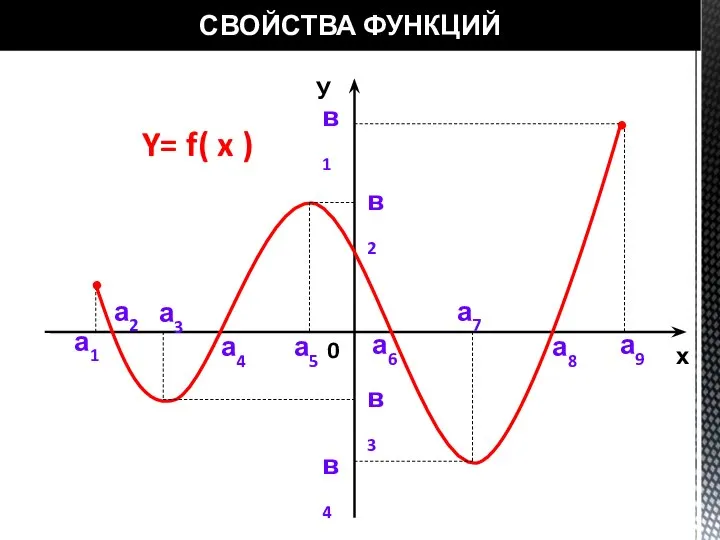
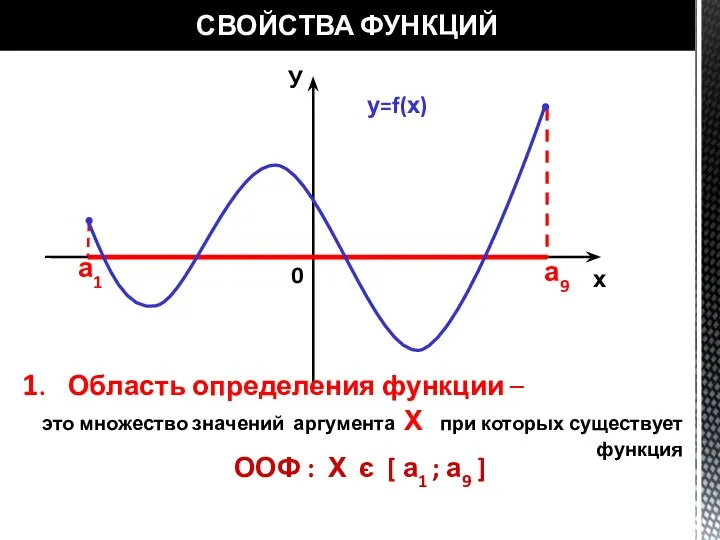
- 16. СВОЙСТВА ФУНКЦИЙ у=f(х) У х 0 а1 а9 1. Область определения функции – это множество значений
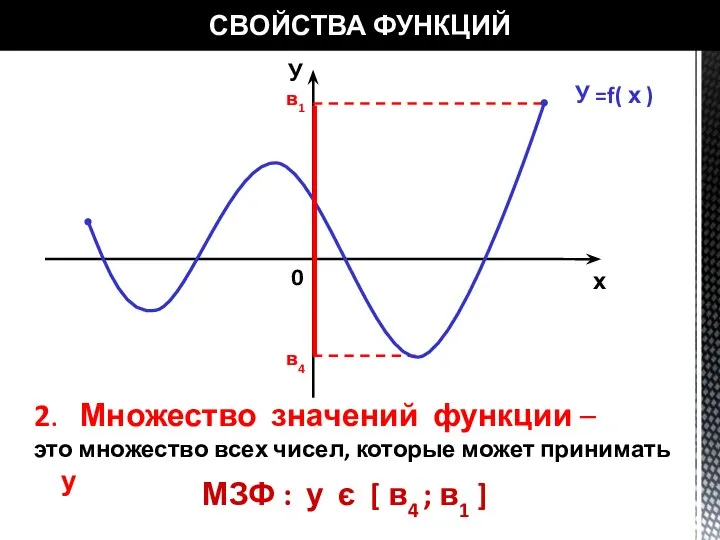
- 17. СВОЙСТВА ФУНКЦИЙ У =f( х ) в1 в4 2. Множество значений функции – это множество всех
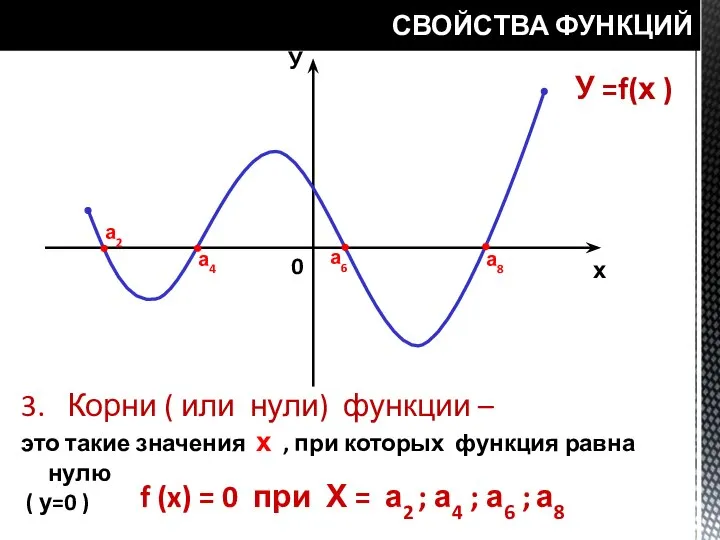
- 18. СВОЙСТВА ФУНКЦИЙ У =f(х ) У х 0 а2 а4 а6 а8 3. Корни ( или
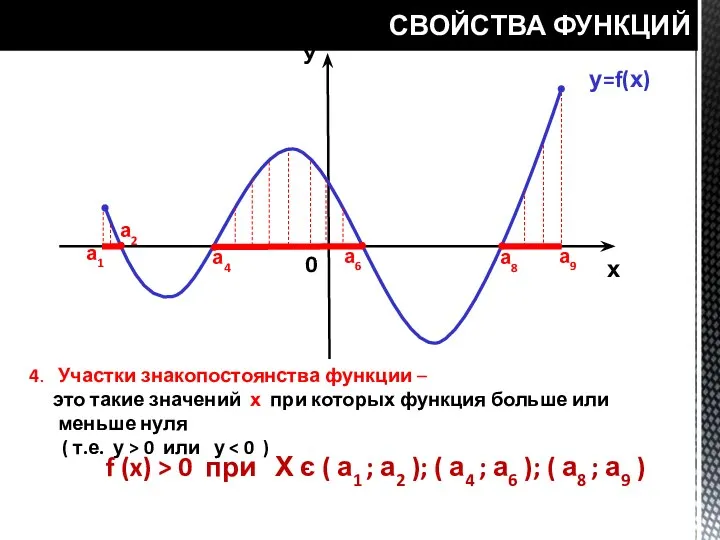
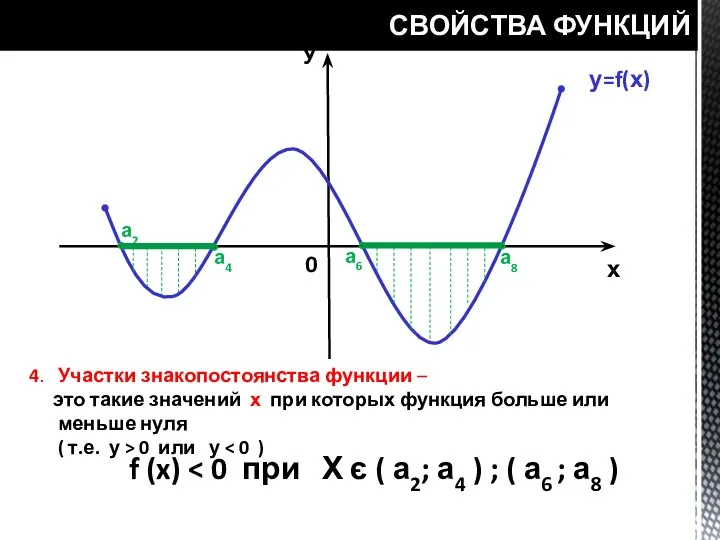
- 19. СВОЙСТВА ФУНКЦИЙ у=f(х) У х 0 а1 а2 а4 а6 а8 а9 4. Участки знакопостоянства функции
- 20. СВОЙСТВА ФУНКЦИЙ у=f(х) У х 0 а2 а4 а6 а8 4. Участки знакопостоянства функции – это
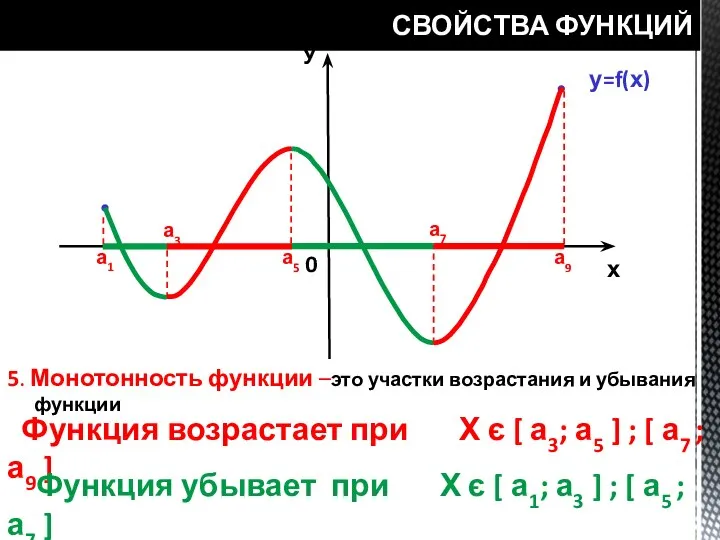
- 21. СВОЙСТВА ФУНКЦИЙ у=f(х) У х 0 а3 а5 а7 а9 5. Монотонность функции –это участки возрастания
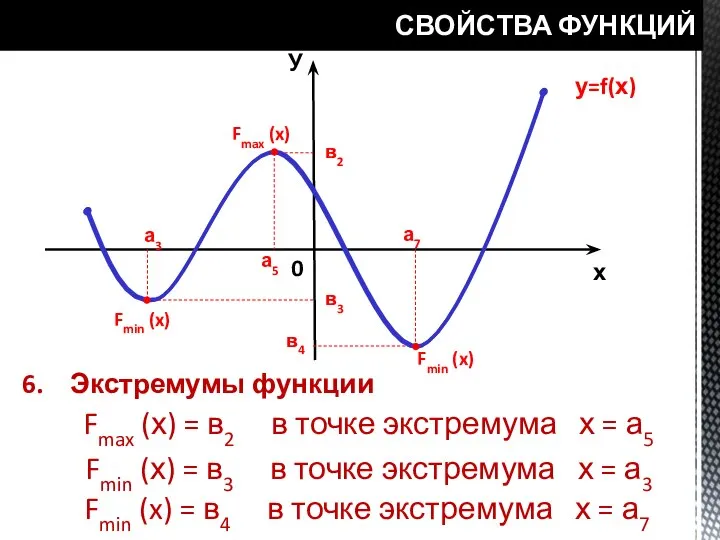
- 22. СВОЙСТВА ФУНКЦИЙ у=f(х) У х 0 а3 а5 а7 в2 в3 в4 Экстремумы функции Fmax (x)
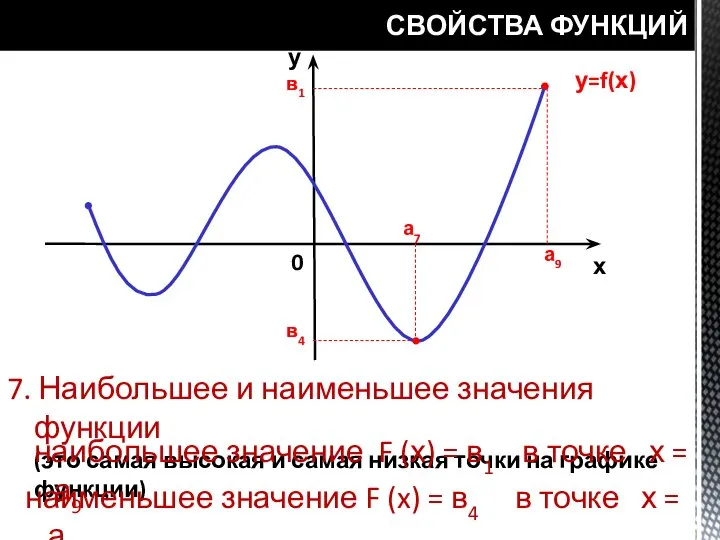
- 23. СВОЙСТВА ФУНКЦИЙ у=f(х) у х 0 а7 а9 в1 в4 7. Наибольшее и наименьшее значения функции
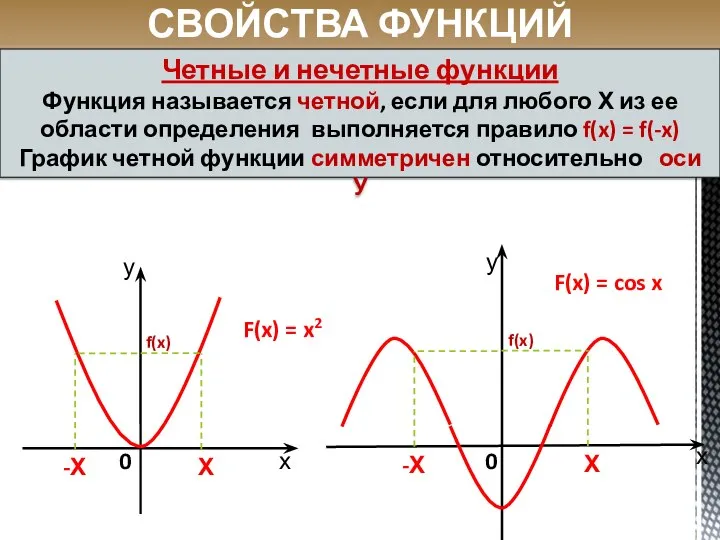
- 24. F(x) = cos x х 0 0 Х -Х СВОЙСТВА ФУНКЦИЙ Четные и нечетные функции Функция
- 25. СВОЙСТВА ФУНКЦИЙ Четные и нечетные функции Функция называется нечетной, если для любого Х из ее области
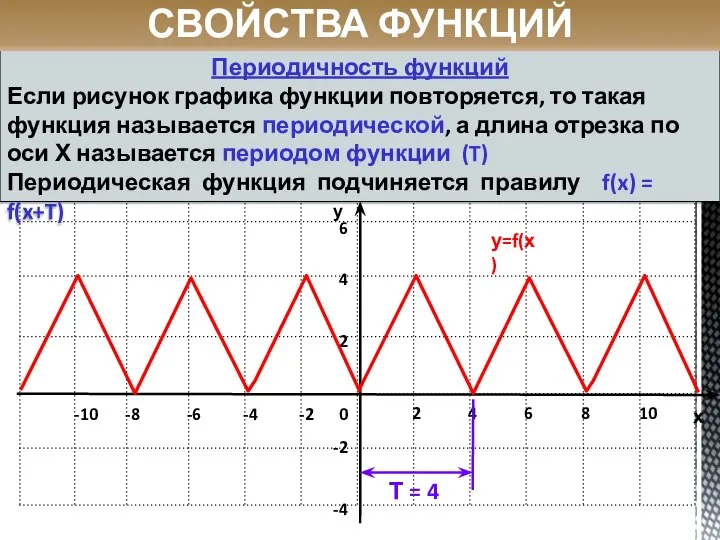
- 26. Периодичность функций Если рисунок графика функции повторяется, то такая функция называется периодической, а длина отрезка по
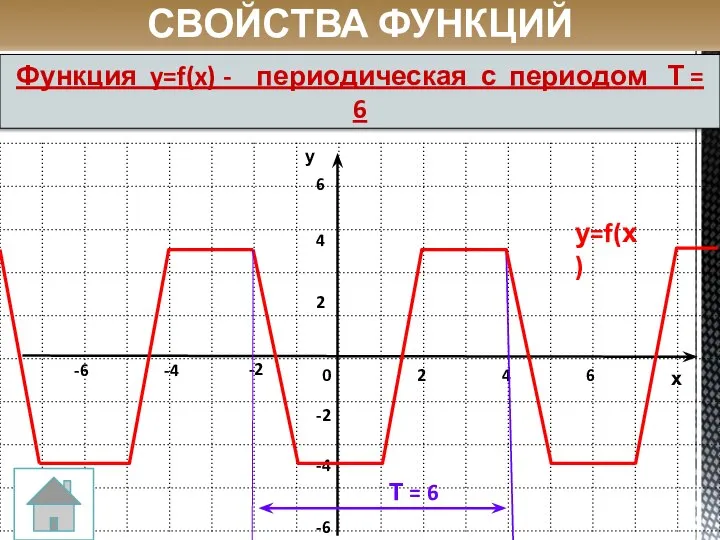
- 27. у=f(х) Т = 6 СВОЙСТВА ФУНКЦИЙ Функция y=f(x) - периодическая с периодом Т = 6
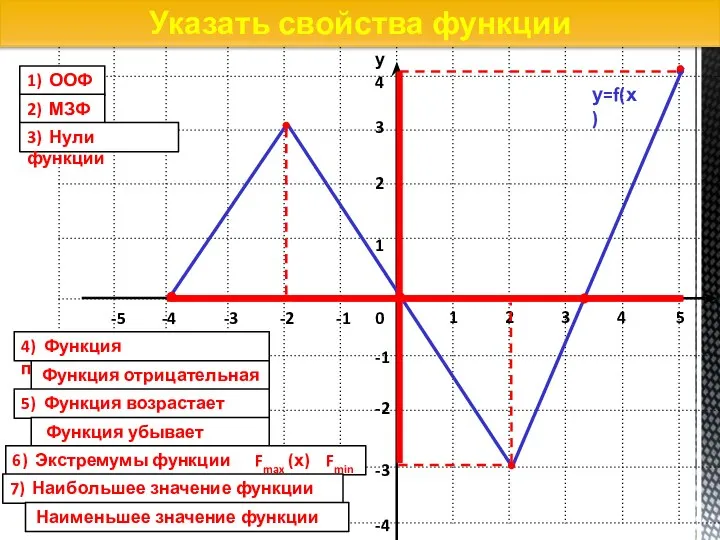
- 28. Указать свойства функции 1) ООФ 2) МЗФ 3) Нули функции 4) Функция положительная Функция отрицательная 5)
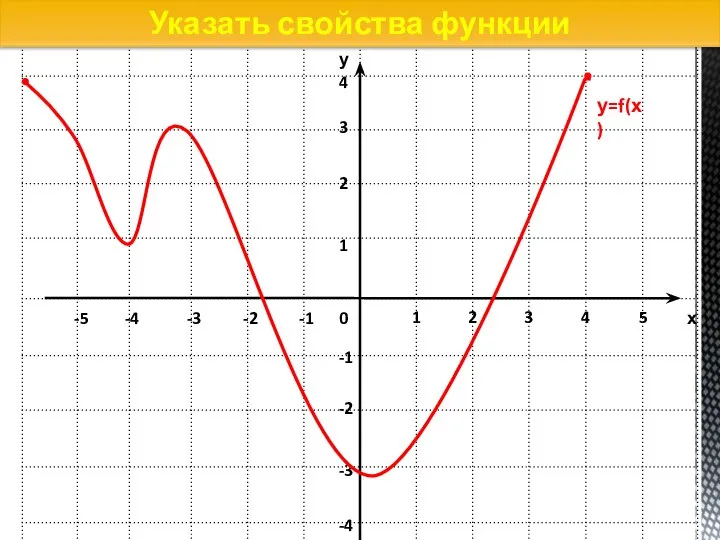
- 29. Указать свойства функции у=f(х)
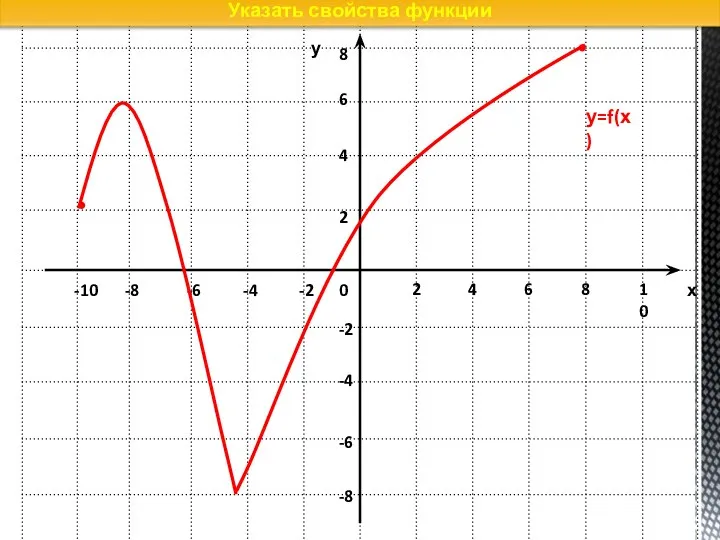
- 30. Указать свойства функции у=f(х)
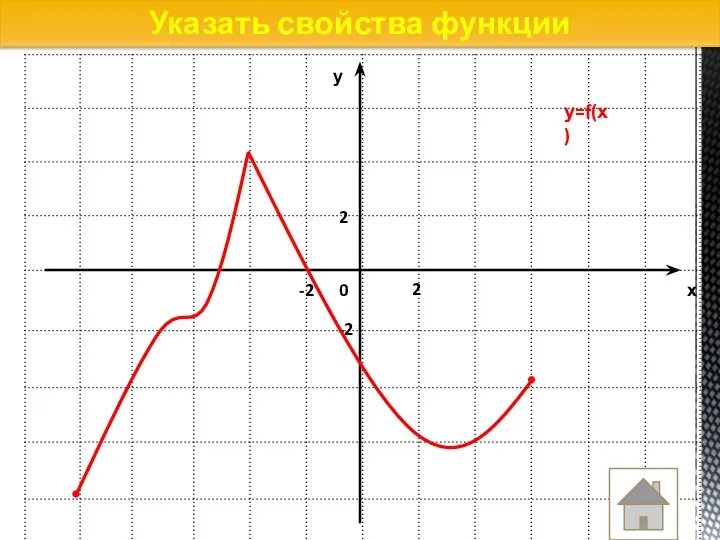
- 31. Указать свойства функции у=f(х)
- 32. Построить график функции Дано: а) Область определения – есть промежуток [-4;3] б) Значения функции составляют промежуток
- 33. ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ФУНКЦИЙ Зная график элементарной функции, например f(x) = x 2 можно построить график «сложной»
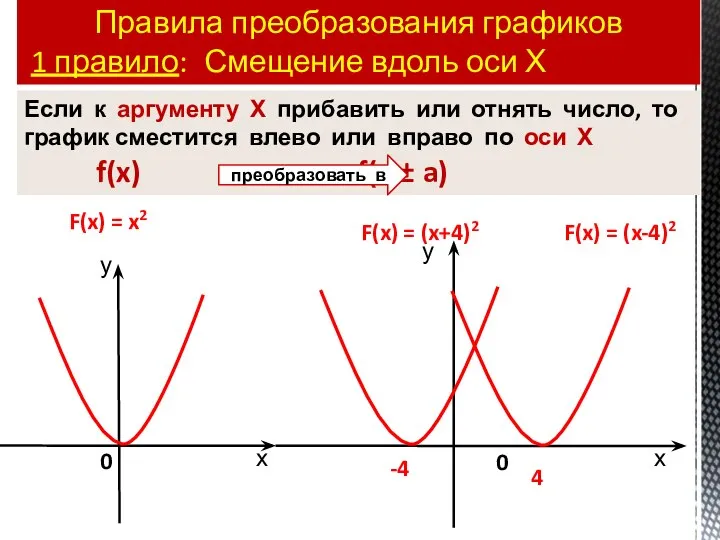
- 34. Правила преобразования графиков 1 правило: Смещение вдоль оси Х 0 0 4 -4 F(x) = x2
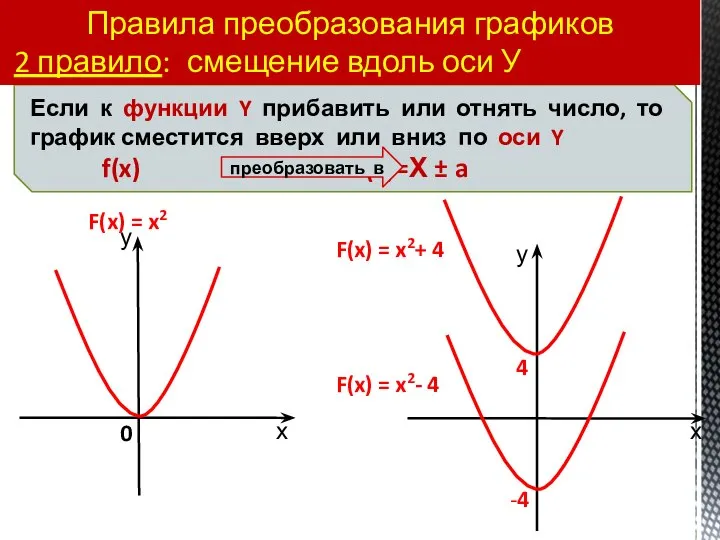
- 35. Правила преобразования графиков 2 правило: смещение вдоль оси У 4 -4 F(x) = x2+ 4 F(x)
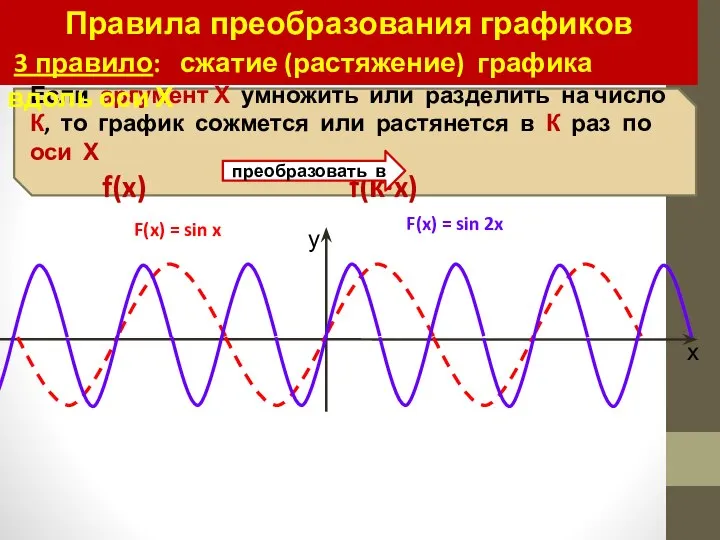
- 36. Правила преобразования графиков 3 правило: сжатие (растяжение) графика вдоль оси Х F(x) = sin x F(x)
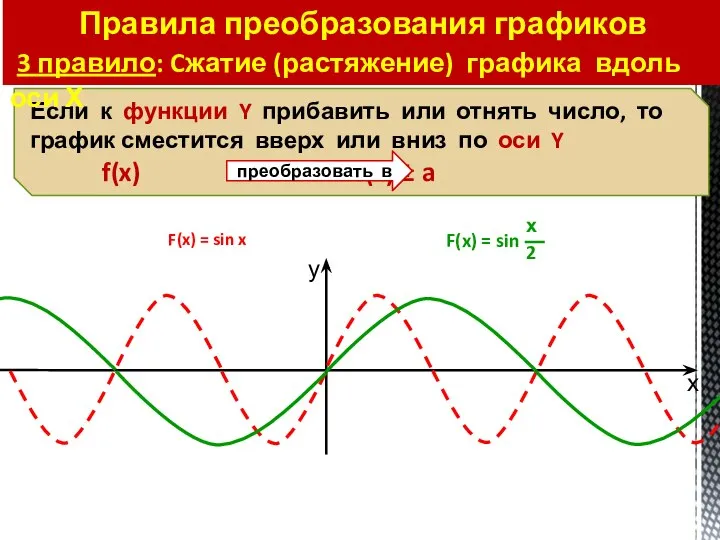
- 37. F(x) = sin x Правила преобразования графиков 3 правило: Cжатие (растяжение) графика вдоль оси Х
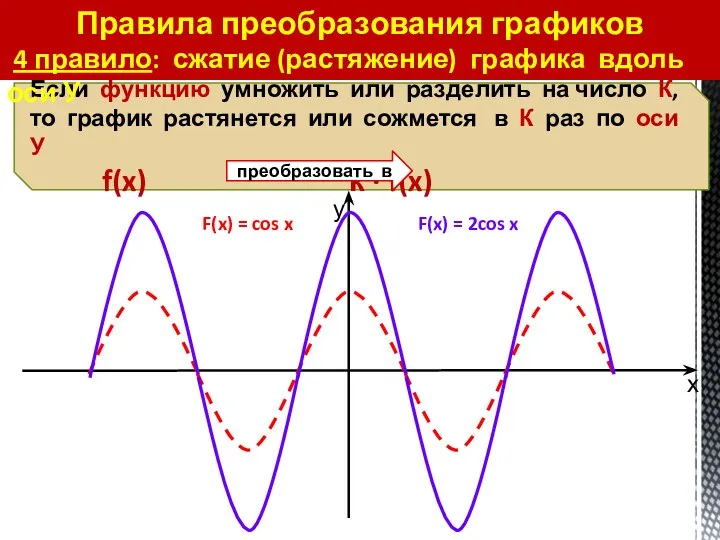
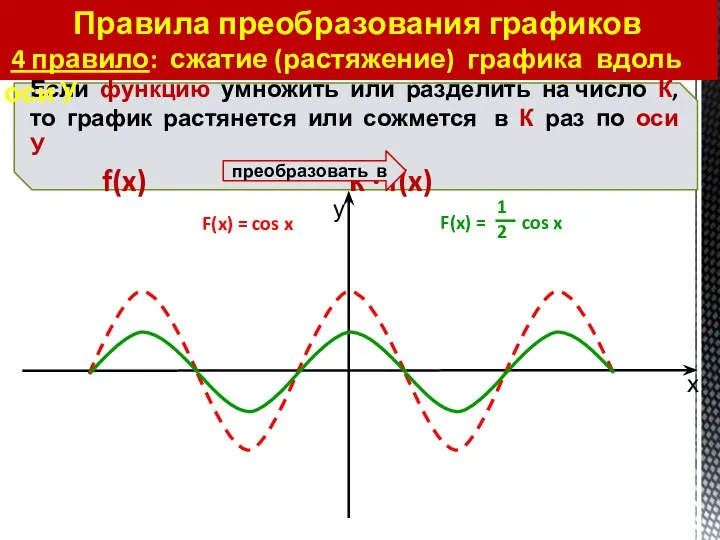
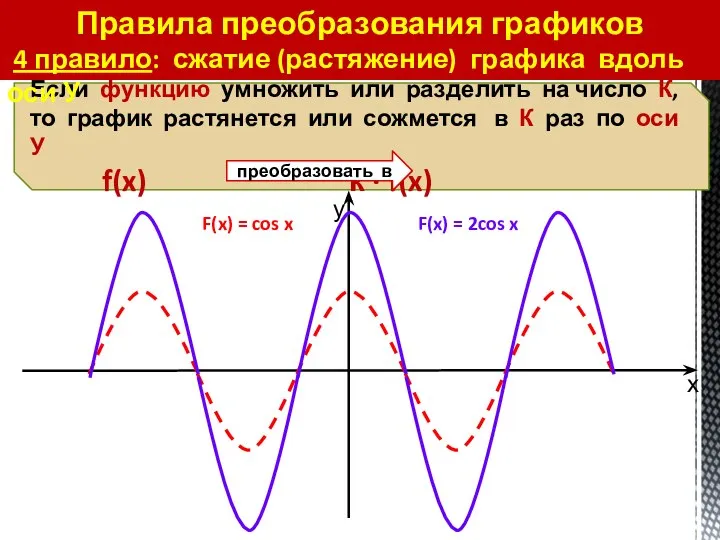
- 38. Правила преобразования графиков 4 правило: сжатие (растяжение) графика вдоль оси У F(x) = cos x F(x)
- 39. Правила преобразования графиков 4 правило: сжатие (растяжение) графика вдоль оси У F(x) = cos x
- 40. Правила преобразования графиков 4 правило: сжатие (растяжение) графика вдоль оси У F(x) = cos x F(x)
- 42. Скачать презентацию



![Построить график функции Дано: а) Область определения – есть промежуток [-4;3] б)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/979678/slide-31.jpg)

 Вписанный угол
Вписанный угол Измеряй и сравнивай
Измеряй и сравнивай Решение заданий с производной
Решение заданий с производной Начальные геометрические сведения. Решение задач
Начальные геометрические сведения. Решение задач Стереометрия. Многогранники
Стереометрия. Многогранники Свойства умножения
Свойства умножения Число. Натуральный ряд. Абсолютная шкала измерений
Число. Натуральный ряд. Абсолютная шкала измерений Биржа знаний
Биржа знаний Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4)
Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (4) Словарь Владимира Ивановича Даля
Словарь Владимира Ивановича Даля Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Правило деления чисел на 1 и на само число
Правило деления чисел на 1 и на само число Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения Дифференцирование и интегрирование функций. ПМиПК-6
Дифференцирование и интегрирование функций. ПМиПК-6 Метод сложения
Метод сложения Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов
Презентация на тему Разложение многочлена на множители с помощью комбинации различных приемов  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Функции. Свойства функций. Математический анализ
Функции. Свойства функций. Математический анализ Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Своя игра. Показательная и степенная функции. 10 класс
Своя игра. Показательная и степенная функции. 10 класс урок 1, урок 2 9кл геом водный урок
урок 1, урок 2 9кл геом водный урок Соединения с повторениями
Соединения с повторениями Проецирование многогранных и кривых поверхностей
Проецирование многогранных и кривых поверхностей Полный факторный эксперимент (ПФЭ)
Полный факторный эксперимент (ПФЭ) Движение по окружности. Подборка задач
Движение по окружности. Подборка задач Основы математической статистики в метрологии. Часть 2
Основы математической статистики в метрологии. Часть 2 Единица длины миллиметр
Единица длины миллиметр