Слайд 2Решение:
Общее число исходов: N=6х6х6=216,
m=6, так как благоприятны события:
6+6+4, 6+4+6,

4+6+6, 5+5+6, 5+6+5, 6+5+5
Р(А)= 1:36=0,03
Ответ: 0,03
Слайд 3Решение: Всего исходов N=2х2х2х2=16. Событие, удовлетворяющее условию, когда все четыре раза выпадет

решка РРРР, значит m=1.
Р(А)=1/16=0,0625
Ответ: 0,0625
Слайд 4Решение: В каждой группе будет по 11 человек. Пусть Михаил попал в

первую группу. Значит любой из оставшихся 32 может попасть в эту группу. В первую группу, кроме Михаила, попадут ещё 10 человек.
N=32, m=10. Р(А)=10/32=0,3125.
Ответ: 0,3125
Слайд 5Решение: Всего сумок: N=136+14=150.
А={сумка окажется с дефектами}, m=14.
Р(А)=14/150=0,09
Ответ: 0,09.

Слайд 6Можно ли решить данную задачи с помощью классического определения вероятности?

Слайд 7ТЕОРЕМЫ СЛОЖЕНИЯ
И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Слайд 11Например: Какова вероятность того, что при одном подбрасывании игрального кубика, выпадет 5

или 6 очков?
Слайд 14Вернемся к задаче:
О КАКИХ СОБЫТИЯХ ИДЁТ РЕЧЬ?

Слайд 15Решение: Возможность выиграть первую и вторую партию не зависят друг от друга.

Вероятность произведения независимых событий равна произведению их вероятностей:
Р(А)=0,45
Р(В)=0,4
Р(АВ)=0,45х0,4=0,18
Ответ: 0,18.
Слайд 16РЕШАЕМ ЗАДАЧИ
НА СЛОЖЕНИЕ И УМНОЖЕНИЕ
ВЕРОЯТНОСТЕЙ


































 Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Степень с рациональным показателем. 11 класс
Степень с рациональным показателем. 11 класс Мотивация … Статистика
Мотивация … Статистика Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Величины. Длина
Величины. Длина Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые 2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию
2Урок обобщения и систематизации знаний. Определение логарифма числа по основанию Презентация на тему Нахождение дроби от числа. Нахождение числа
Презентация на тему Нахождение дроби от числа. Нахождение числа  Параллельные прямые в пространстве
Параллельные прямые в пространстве Основы геометрии (5 класс)
Основы геометрии (5 класс) Экстремум функции. Признак постоянства функции. Исследование на экстремум
Экстремум функции. Признак постоянства функции. Исследование на экстремум Равносильность формул
Равносильность формул Аналитическая геометрия на плоскости (лекция 1-2)
Аналитическая геометрия на плоскости (лекция 1-2) Пространственные тела. Многогранники
Пространственные тела. Многогранники Приближенное решение уравнений
Приближенное решение уравнений Понятие вектора в пространстве
Понятие вектора в пространстве Сумма углов в треугольнике
Сумма углов в треугольнике Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс) Соединения с повторениями
Соединения с повторениями Функция
Функция ЕГЭ Профиль. Решение задания №12
ЕГЭ Профиль. Решение задания №12 Применение тактильных приемов при изучении геометрического материала в 5 классе
Применение тактильных приемов при изучении геометрического материала в 5 классе Компьютерный и интеллектуальный анализ данных. Теория вероятностей
Компьютерный и интеллектуальный анализ данных. Теория вероятностей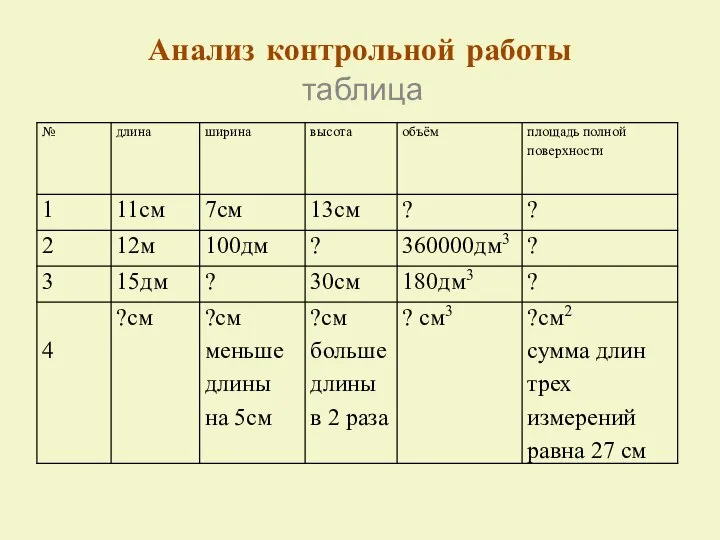 Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Понятие цилиндра
Понятие цилиндра Преобразование графиков функций. 8 класс
Преобразование графиков функций. 8 класс Типи трикутників
Типи трикутників Производные функции нескольких переменных (часть 1)
Производные функции нескольких переменных (часть 1)