Алгебраические методы решения прикладных задач на экстремум Материал к внеклассным занятиям по математике в 10-12 классах

Алгебраические методы решения прикладных задач на экстремум
В технике и естествознании, как, впрочем, и в обыденной жизни, встречается особый вид задач – задач на «максимум и минимум».
Люди издавна желали получить наибольшую выгоду при наименьших затратах.
Огромное число таких задач возникает в экономике и технике. Бурное развитие экономики и техники привело к новой теории – теории оптимального управления.
В математике эти задачи называют задачами на экстремум. Исследование задач на экстремум началось 25 веков назад.
С возникновением математического анализа были созданы общие методы их решения.

Метод, основанный на теореме о произведении двух сомножителей,
сумма которых постоянна
Теорема Произведение двух множителей, сумма которых постоянна, имеет наибольшее значение при равенстве множителей:
max при

Пример 1 решения задач на экстремум
Из квадратного листа картона с заданной стороной нужно изготовить квадратную коробку, вырезая по углам листа равные квадраты и загибая образовавшиеся края.
Какой величины должна быть сторона каждого вырезанного квадрата, чтобы объем сделанной коробки был наибольшим?

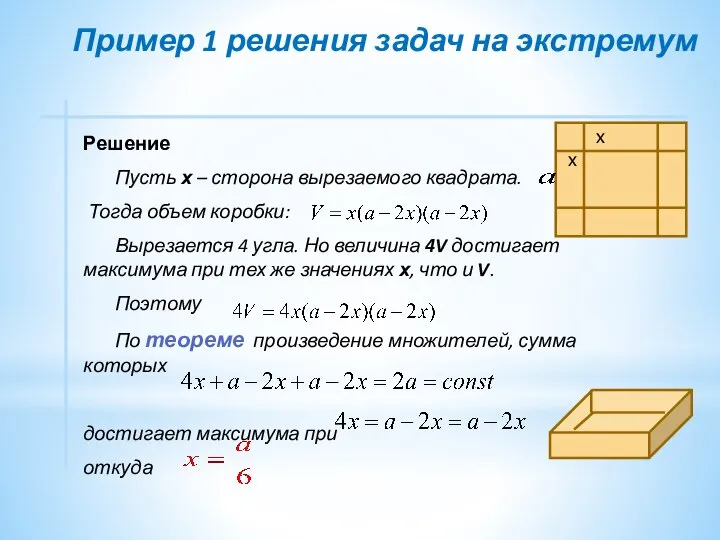
Решение
Пусть х – сторона вырезаемого квадрата.
Тогда объем коробки: Вырезается 4 угла. Но величина 4V достигает максимума при тех же значениях х, что и V.
Поэтому
По теореме произведение множителей, сумма которых
достигает максимума при
откуда
Пример 1 решения задач на экстремум

Пример 2 решения задач на экстремум
Окно имеет форму прямоугольника, завершенного полукругом. При заданном периметре найти размеры окна, чтобы оно пропускало наибольшее количество света.

Пример 2 решения задач на экстремум

Метод, основанный на теореме о сумме
2-х положительных слагаемых,
произведение которых постоянно
Теорема
Сумма двух положительных слагаемых, произведение которых постоянно, имеет наименьшее значение при равных слагаемых
при