Слайд 2Окружность
Во многих задачах встречается окружность, касающаяся сторон угла. Напомним, что в этом
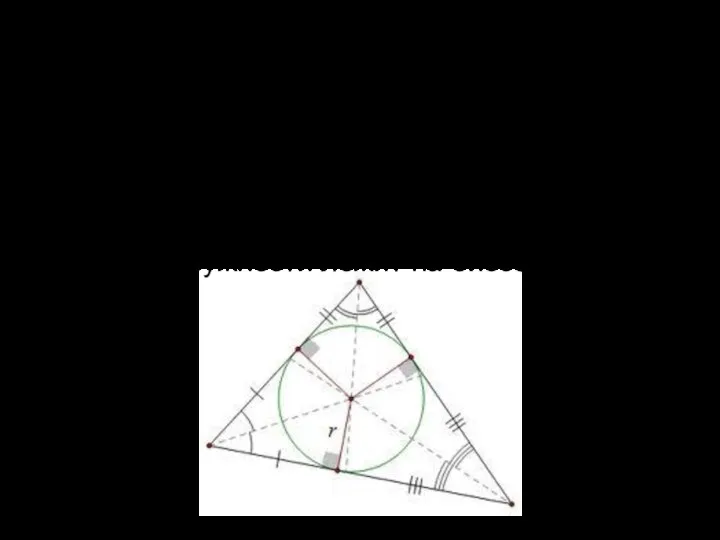
случае:
Центр окружности лежит на биссектрисе угла
Слайд 3Окружность
Отрезки, соединяющие точки касания с центром окружности, являются её радиусами и перпендикулярны
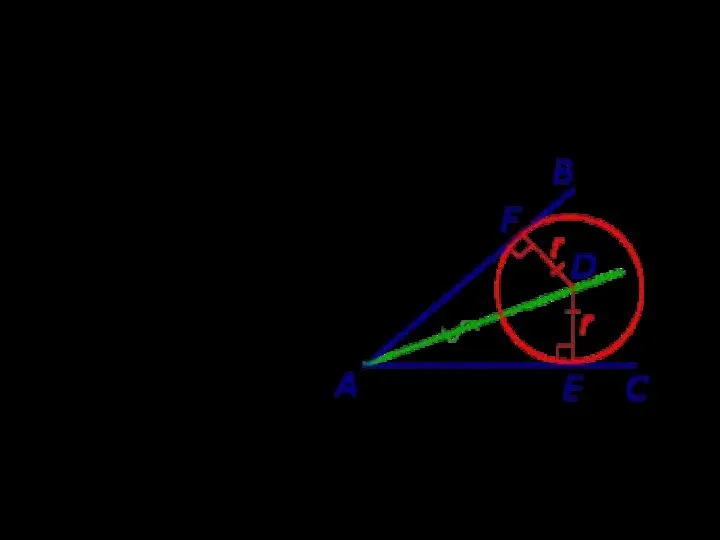
к сторонам угла
Слайд 4Окружность
Расстояния от вершины угла до точек касания равны
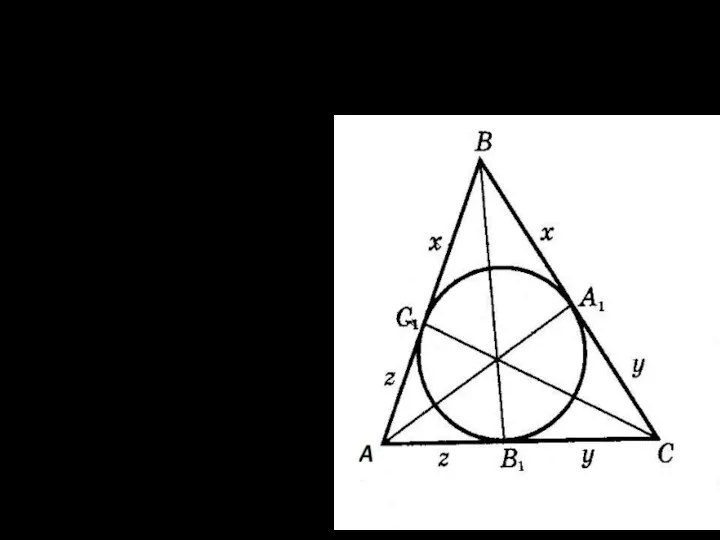
Слайд 5Окружность
Угол KAM + Угол KOM = 180°
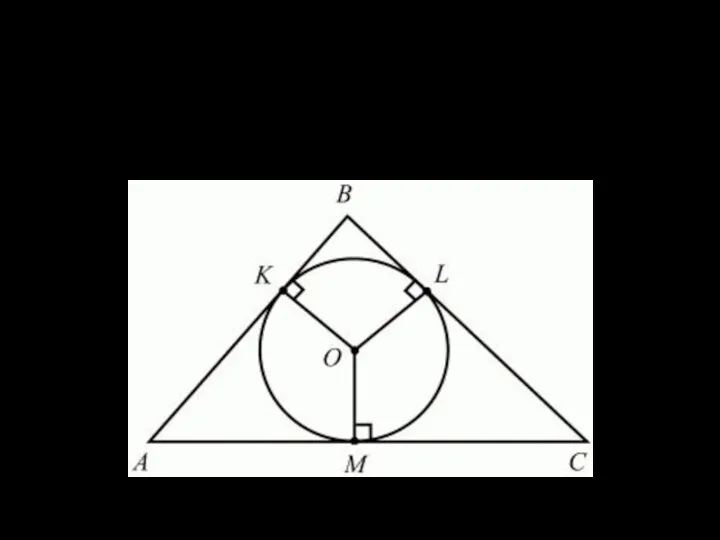
Слайд 6Проверь себя
Окружность с центром D касается сторон угла A в точках F
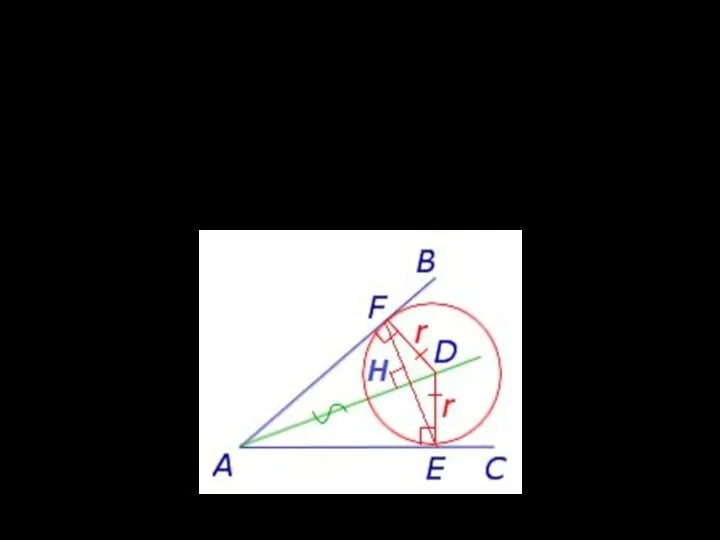
и E. Радиус окружности равен 7. AD = 25. Найдите FE.
Слайд 7Решение
Т. к. DF перпендикулярна AF, то в треугольнике AFD
AF = √(AD2 —

FD2) = √(252 — 72) = 24
Тогда AE = AF = 24
В треугольнике AFE отрезок AH — биссектриса и AF = AE, следовательно, AH перпендикулярна FE и FH = HE.
Найдем высоту FH прямоугольного треуголника AFD:
Слайд 8Решение
FH * AD = AF * FD
FH = (7 * 24) /

25 = 6,72
Тогда FE = 2FH = 13,44
Ответ: 13,44
Слайд 9Задание №2
К окружности с центром O проведена секущая AO и касательная AB.
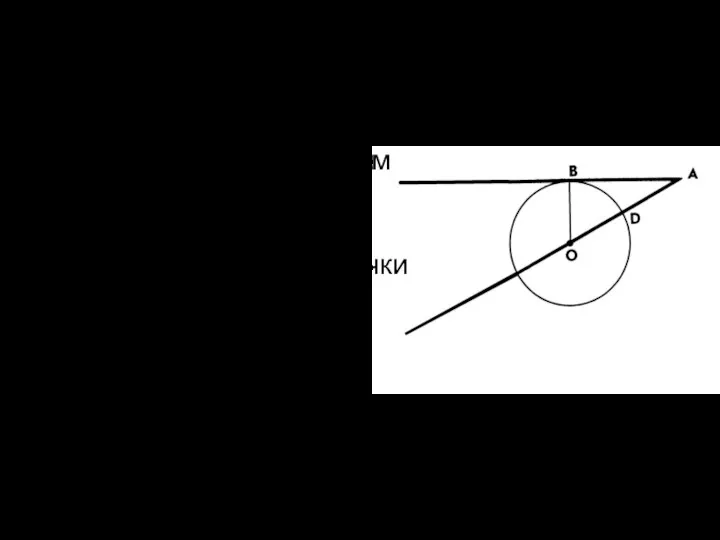
Расстояние от A до точки касания равна 40, расстояние от до D равно 20. Найдите радиус окружности, которая касается прямых AB и AO и отрезка OB.
Слайд 10Решение
Обозначим AD = a, AB = l, OB = R, O1K =
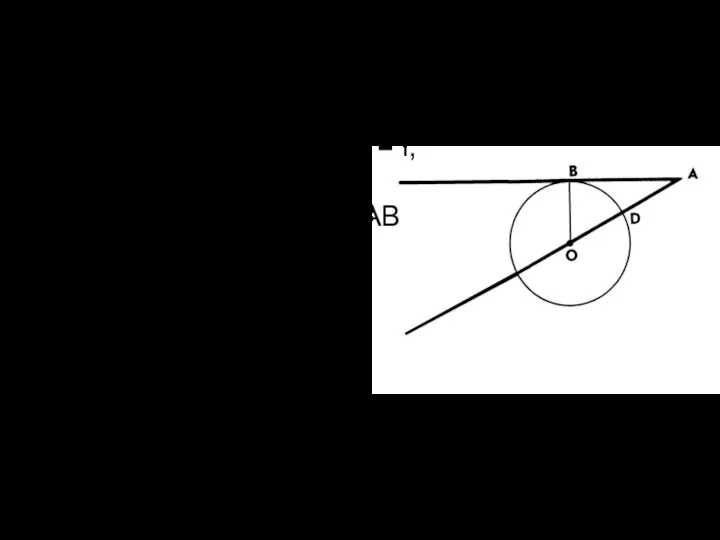
r. OB перпендикулярна AB треугольник AOB прямоугольный.
AB2 + OB2 = OA2
R2 + l2 = (R2 + a2)
l2 = 2aR + a2
R = (l2 — a2) / 2a = (402 — 202) / 2 * 20 = 30
Слайд 11Случай №1
Найдем радиус r окружности, вписанной в треугольник ABO.
2r + 2AO
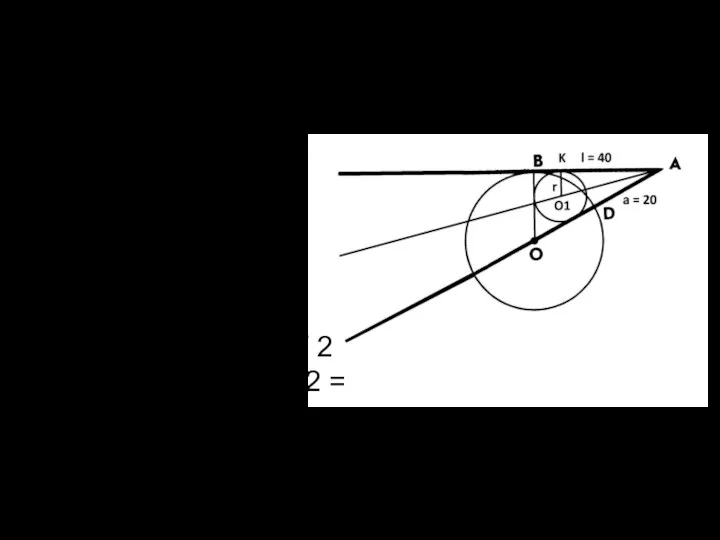
= PAOB
r = (PAOB — 2AO) / 2 = (120 — 2 * 50) / 2 = 10
Слайд 13Случай №2
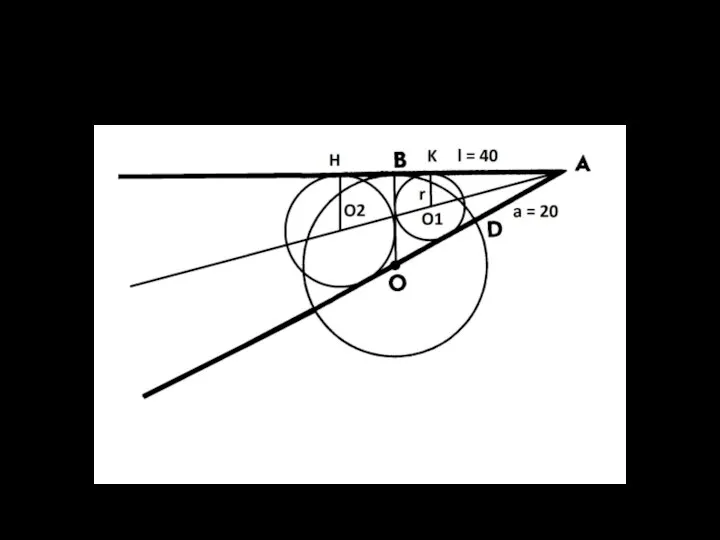
Окружность касается треугольника OBA внешним образом (продолжения AB и AD). Центры
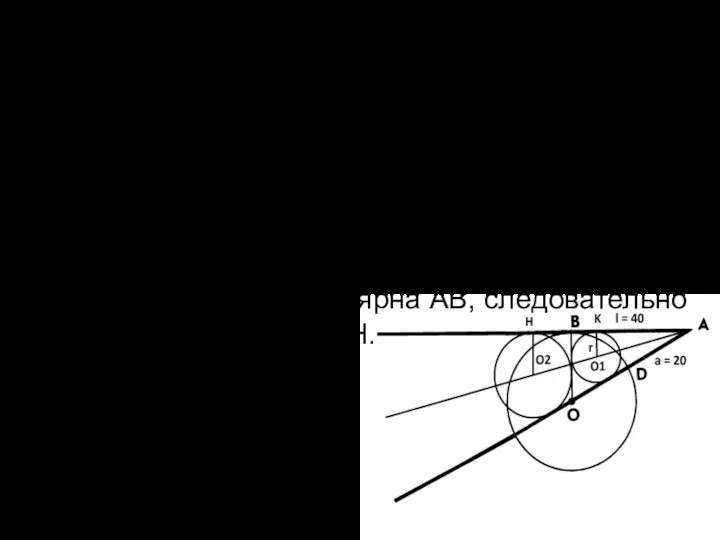
окружностей в 1 и 2 случаях лежат на биссектрисе угла BAO, O1K перпендикулярна AB, O2H перпендикулярна АВ, следовательно O1K параллельна O2H.











 Приемы вычитания с переходом через разряд вида 35 - 7
Приемы вычитания с переходом через разряд вида 35 - 7 Модуль Начертательная геометрия. Тема 6
Модуль Начертательная геометрия. Тема 6 Знакомство с подсчётом вероятности
Знакомство с подсчётом вероятности Признаки параллелограмма
Признаки параллелограмма Презентация на тему ДЕЛЕНИЕ
Презентация на тему ДЕЛЕНИЕ  Динамика системы вблизи цикла
Динамика системы вблизи цикла История происхождения математических знаков
История происхождения математических знаков Пирамида Кукулькана – величайший храм майя
Пирамида Кукулькана – величайший храм майя Монотонность функции
Монотонность функции Преобразование произведений тригонометрических функций в сумму. Математическая игра Интеллектуальные гонки
Преобразование произведений тригонометрических функций в сумму. Математическая игра Интеллектуальные гонки Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Линейная функция
Линейная функция Простейшие геометрические фигуры
Простейшие геометрические фигуры Радианная мера угла. Синус, косинус, тангенс числа
Радианная мера угла. Синус, косинус, тангенс числа Основы анализа данных. Метод наименьших квадратов. (Лекция 6)
Основы анализа данных. Метод наименьших квадратов. (Лекция 6)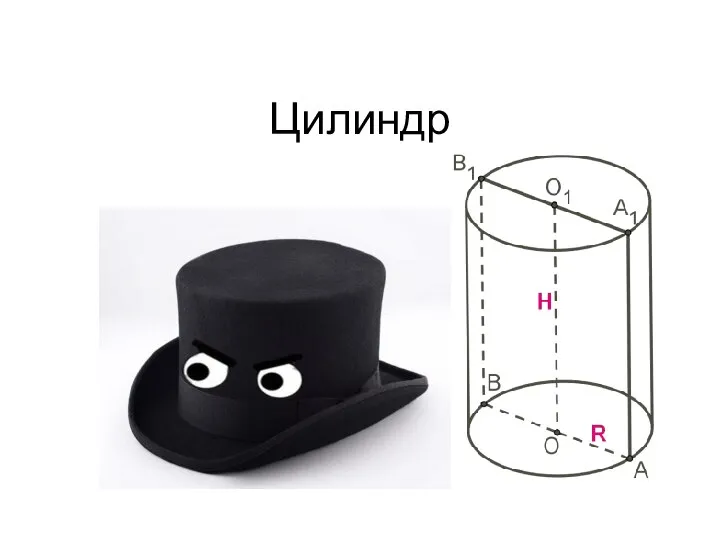 Цилиндр. Формулы цилиндра
Цилиндр. Формулы цилиндра Дроби и проценты. Построение диаграмм
Дроби и проценты. Построение диаграмм Сложение и вычитание дробей
Сложение и вычитание дробей Степень с натуральным показателем. Занимательные задания
Степень с натуральным показателем. Занимательные задания Отношения и пропорции. Золотое сечение
Отношения и пропорции. Золотое сечение Прогрессия. Анзац
Прогрессия. Анзац Геометрическое место точек. Построение серединного перпендикуляра и биссектриссы данного угла
Геометрическое место точек. Построение серединного перпендикуляра и биссектриссы данного угла Изучение конструкции в геометрии токарного резца
Изучение конструкции в геометрии токарного резца Презентация на тему Обозначение и сравнение углов
Презентация на тему Обозначение и сравнение углов  Учимся писать цифры
Учимся писать цифры Вывод формулы длины окружности и площади круга
Вывод формулы длины окружности и площади круга Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Исследовательская работа Загадки треугольника. 9 класс
Исследовательская работа Загадки треугольника. 9 класс