Решение комбинаторных задач

о
м
б
07.05.2021
и
н
а
т
о
р
и
к
а
Термин «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Комбинаторика
- это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
к

Что значит решить
комбинаторную задачу?
Решить комбинаторную задачу - это значит выписать или сосчитать все возможные комбинации (способы, варианты) составленные из объектов (цифр, букв, чисел, слов, предметов и др.,) отвечающих условию задачи.

На завтрак в школьной столовой можно выбрать кашу манную, гречневую, овсяную или рисовую, запить можно чаем с лимоном, какао или соком морковным. Сколько вариантов завтрака есть?

Выбор напитка – выбор объекта А
Выбор каши - выбор объекта В
Объект А имеет 3 варианта выбора, а объект В - 4,
вариантов выбора пары объектов А и В 3•4=12.

ПРАВИЛО УМНОЖЕНИЯ
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А и В) ,в указанном порядке, можно осуществить
m●n способами.
При этом число способов выбора второго объекта не зависит от того, как именно выбран первый объект.

Решите задачу
Сколько может быть различных комбинаций выпавших
граней при бросании двух игральных костей?
Решение:
На первой кости может быть: 1,2,3,4,5 и 6 очков, т.е. 6 вариантов.
На второй – 6 вариантов.
Всего: 6*6=36 вариантов.
Ответ: всего 36 комбинаций

ИГРА«Орлянка»
Монету подбрасывают три раза.
ООО
ООР
ОРО
ОРР
РОО
РОР
РРО
РРР
МОНЕТА
Решение : 2·2·2 = 8
I подбрасывание
I I подбрасывание
III подбр.
Дерево возможных вариантов

Комбинаторные задачи на умножение.
Имеется 3 вида конвертов и 4 вида марок. Сколько существует вариантов выбора конверта с маркой?
В кружке 6 учеников. Сколькими способами можно выбрать старосту кружка и его заместителя?
В буфете есть 4 сорта пирожков (не меньше двух штук каждого сорта). Сколькими способами ученик может купить себе 2 пирожка?
Сколько все трехзначных числел, в записи которых используются цифры 0,1,2 при условии, что:
1)Все цифры в числах разные
2)Цифры в числах могут повторяться
Решение: 6 · 5 = 30
Решение: 3 · 4 = 12
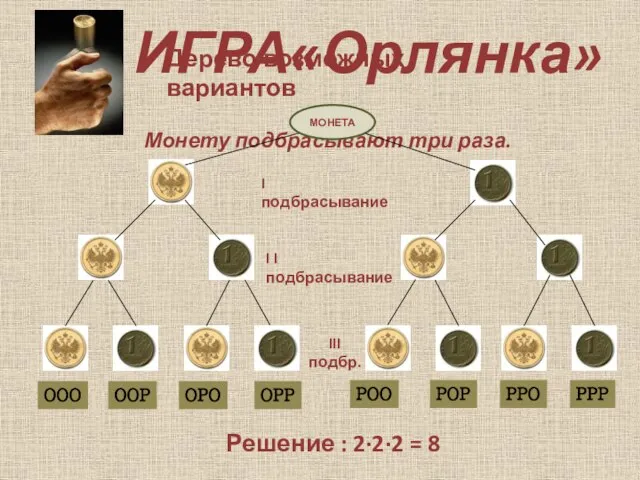
Решение: 2 · 3 · 3 = 18
Решение: 4 · 4 = 16
Решение: 2 · 2 · 1 = 4

Задача.При встрече каждый из друзей пожал другому руку (каждый пожал каждому). Сколько рукопожатий было сделано, если друзей было:
1)трое 2)четверо 3)пятеро
Подсчет вариантов с помощью графов
Решать некоторые математические задачи помогают специальные схемы, состоящие из точек и соединяющих их дуг или стрелок. Такие схемы называют графами, точки называют вершинами графа, а дуги – рёбрами графа.