Содержание
- 2. Содержание Связи между понятиями Бинарное отношение Определение функции Виды функций Операции Построение функций Свойства бинарных отношений
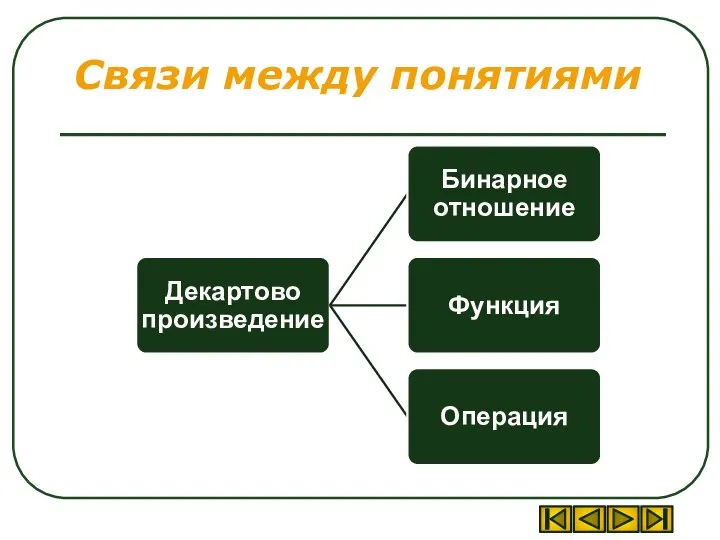
- 3. Связи между понятиями
- 4. Бинарное отношение Бинарным отношением Т(М) на множестве М называется подмножество , Инфиксная форма записи бинарного отношения
- 5. Виды бинарных отношений Обратное отношение Дополнительное отношение
- 6. Виды бинарных отношений Тождественное отношение Универсальное отношение
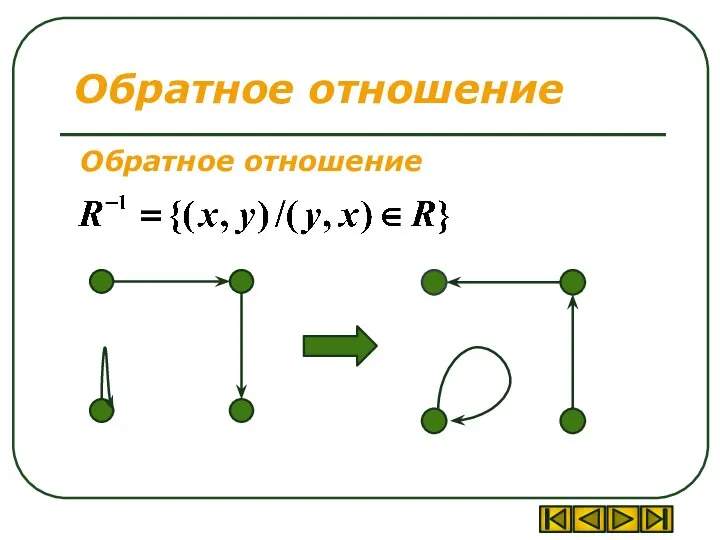
- 7. Обратное отношение Обратное отношение
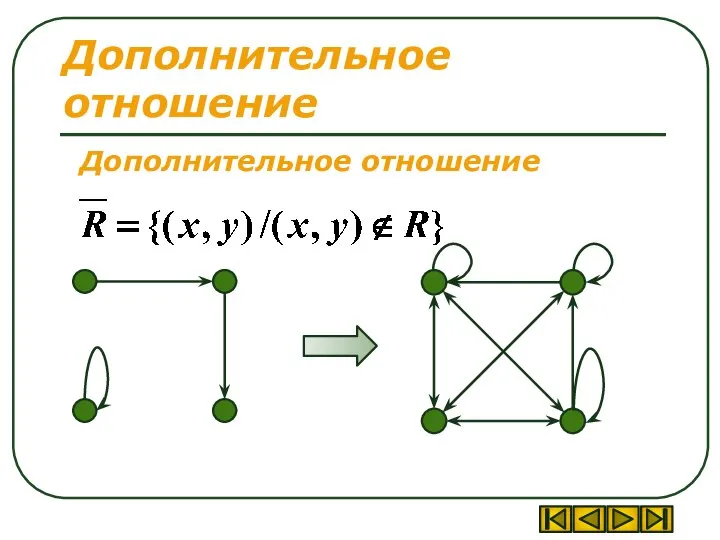
- 8. Дополнительное отношение Дополнительное отношение
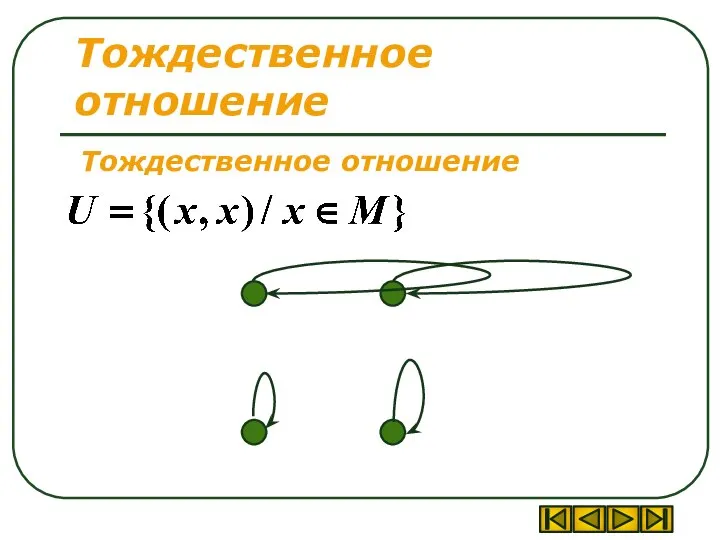
- 9. Тождественное отношение Тождественное отношение
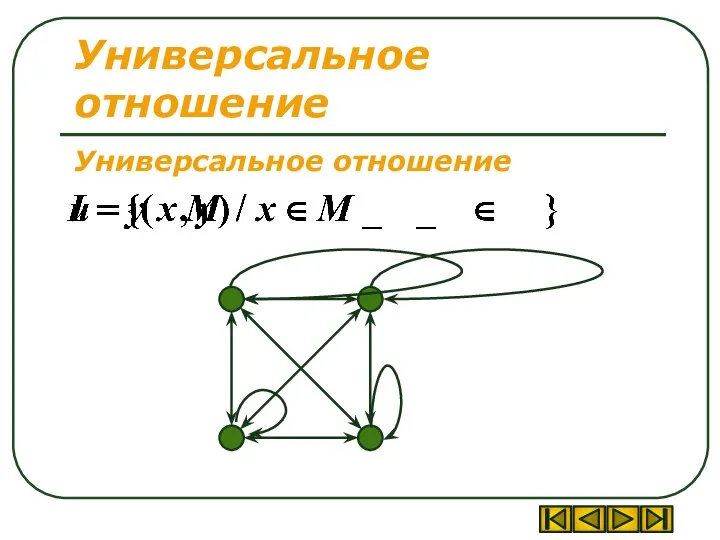
- 10. Универсальное отношение Универсальное отношение
- 11. Функция называется функцией, если для каждого элемента х найдется не более одного элемента у такого, что
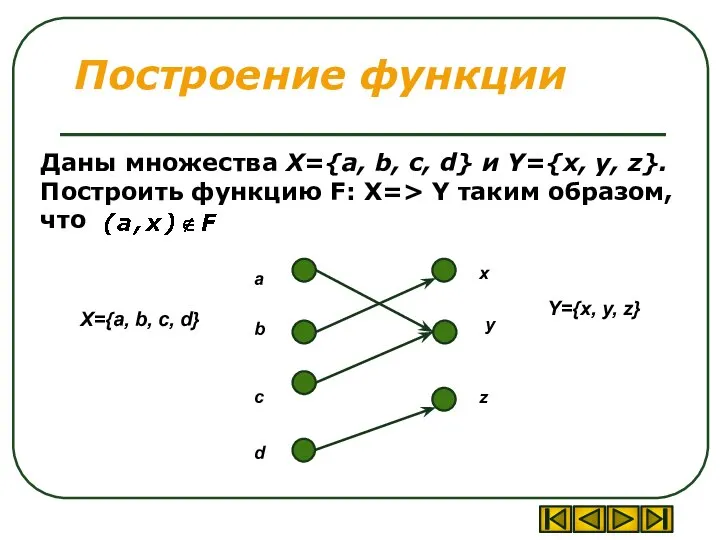
- 12. Построение функции Даны множества X={a, b, c, d} и Y={x, y, z}. Построить функцию F: X=>
- 13. Инъекция Функция F: X →Y называется инъективной (инъекцией или вложением), если она переводит разные элементы Х
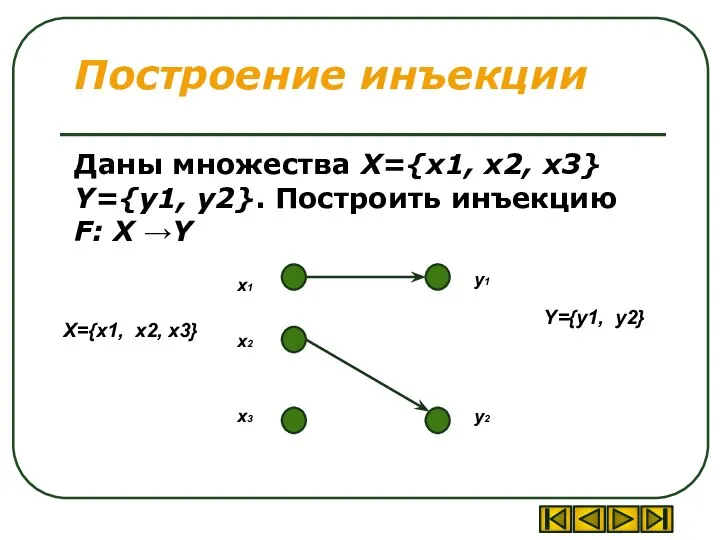
- 14. Построение инъекции Даны множества X={x1, x2, x3} Y={y1, y2}. Построить инъекцию F: X →Y
- 15. Сюръекция Функция F: X → Y называется сюръективной (сюръекцией или наложением), если множество ее значений есть
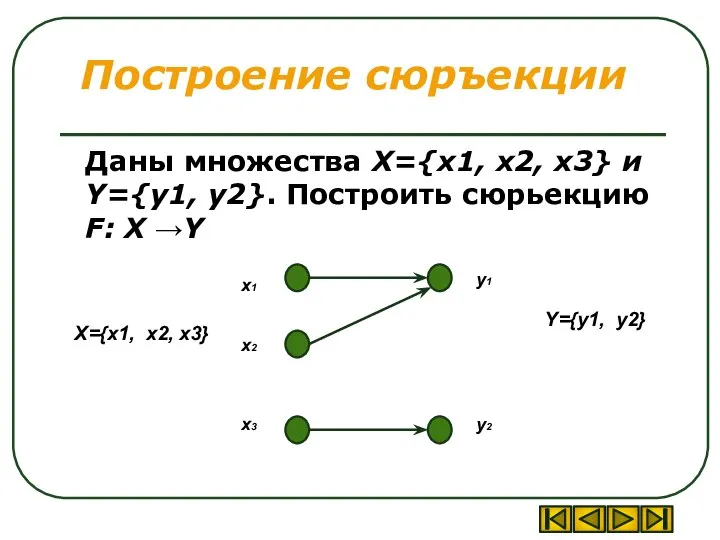
- 16. Построение сюръекции Даны множества X={x1, x2, x3} и Y={y1, y2}. Построить сюрьекцию F: X →Y
- 17. Биекция Функция F: X →Y называется биекцией или взаимно однозначным соответствием, если она одновременно является инъекцией
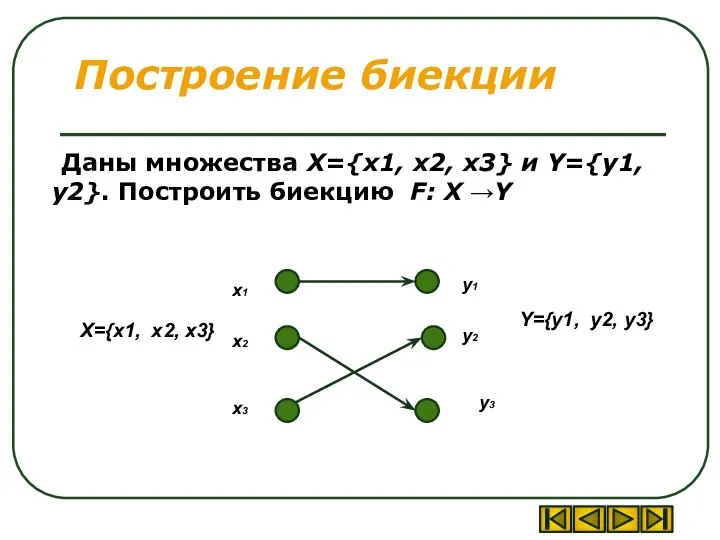
- 18. Построение биекции Даны множества X={x1, x2, x3} и Y={y1, y2}. Построить биекцию F: X →Y y3
- 19. Операция Частным случаем функции является операция О В этом случае область значения Х и область определения
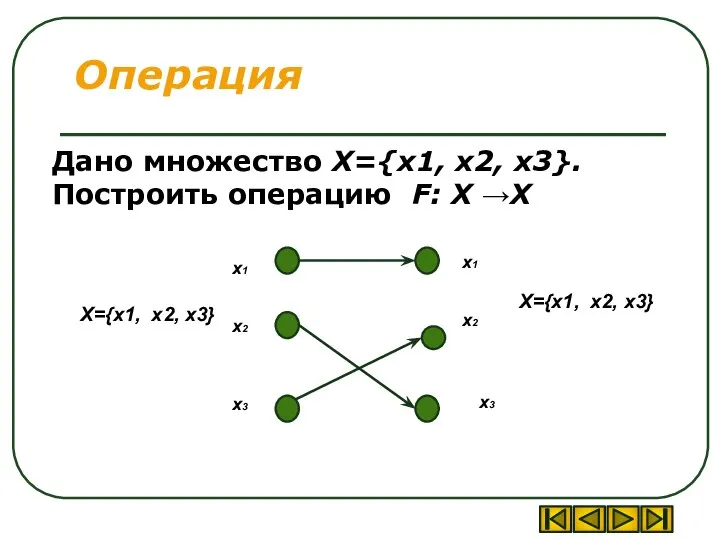
- 20. Операция Дано множество X={x1, x2, x3}. Построить операцию F: X →X x3
- 21. Решение задач Дано множество натуральных чисел N. Укажите, какие из арифметических действий (сложение, вычитание, умножение, деление)
- 22. Решение задач Дано множество натуральных чисел N. Укажите, какие из арифметических действий (сложение, вычитание, умножение, деление)
- 23. Решение задач На множестве натуральных чисел задана О операция. Какой может быть эта операция? а) a
- 24. Решение задач На множестве натуральных чисел задана О операция. Какой может быть эта операция? а) a
- 25. Решение задач На множестве рациональных чисел задана О операция . Какой может быть эта операция? а)
- 26. Решение задач На множестве рациональных чисел задана О операция . Какой может быть эта операция? а)
- 27. Бинарное отношение T(M), называется рефлексивным тогда и только тогда, когда для каждого элемента пара (х, х)
- 28. Бинарное отношение T(M) называется иррефлексивным тогда и только тогда, когда для каждого элемента пара (х, х)
- 29. Если бинарное отношение T(M) не обладает ни свойством рефлексивности, ни свойством иррефлексивности, то оно является нерефлексивным
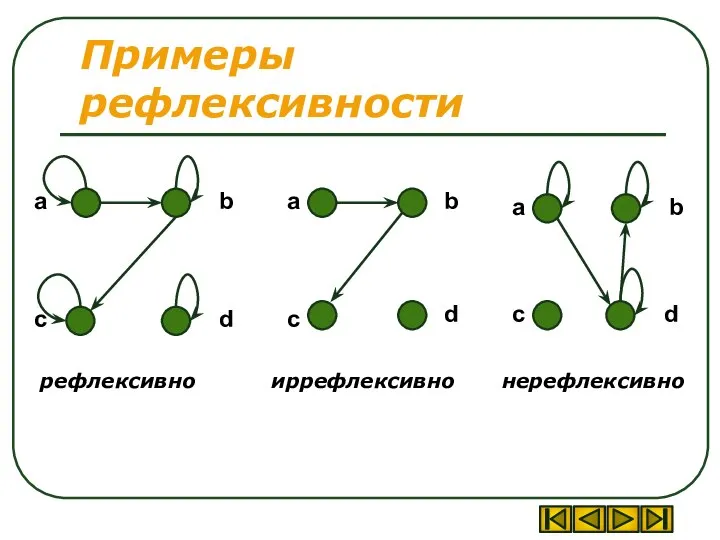
- 30. Примеры рефлексивности рефлексивно иррефлексивно нерефлексивно
- 31. Симметричность Бинарное отношение T(M) называется симметричным тогда и только тогда, когда для каждой пары различных элементов
- 32. Антисимметричность Бинарное отношение T(M) называется антисимметричным тогда и только тогда, когда для каждой пары различных элементов
- 33. Другое определение антисимметричности Бинарное отношение T(M) называется антисимметричным тогда и только тогда, когда из того, что
- 34. Если бинарное отношение T(M) не обладает ни свойством симметричности, ни свойством антисимметричности, то оно является несимметричным
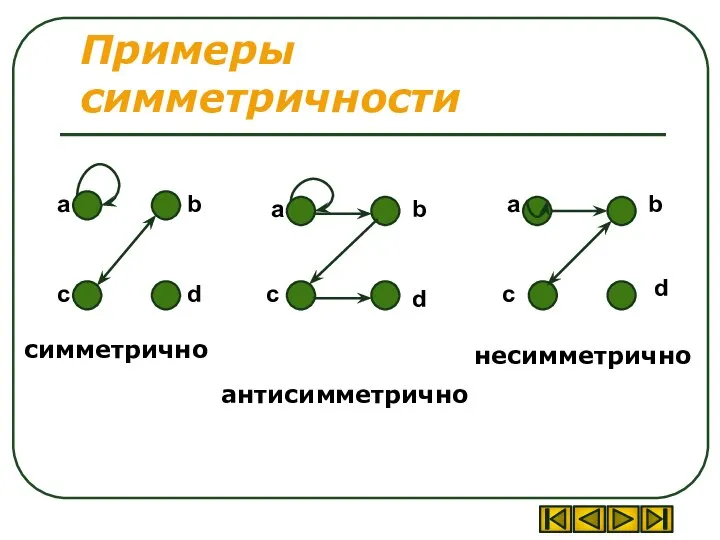
- 35. Примеры симметричности симметрично антисимметрично а b d
- 36. Транзитивность Бинарное отношение T(M) называется транзитивным тогда и только тогда, когда для каждых двух пар различных
- 37. Бинарное отношение T(M) называется интранзитивным тогда и только тогда, когда для каждых двух пар различных элементов
- 38. Если бинарное отношение T(M) не обладает ни свойством транзитивности, ни свойством интранзитивности, то оно является нетранзитивным
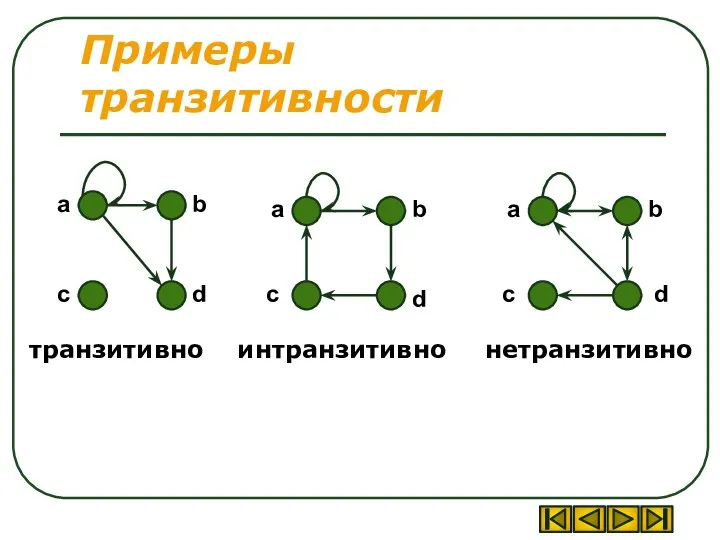
- 39. Примеры транзитивности транзитивно нетранзитивно интранзитивно
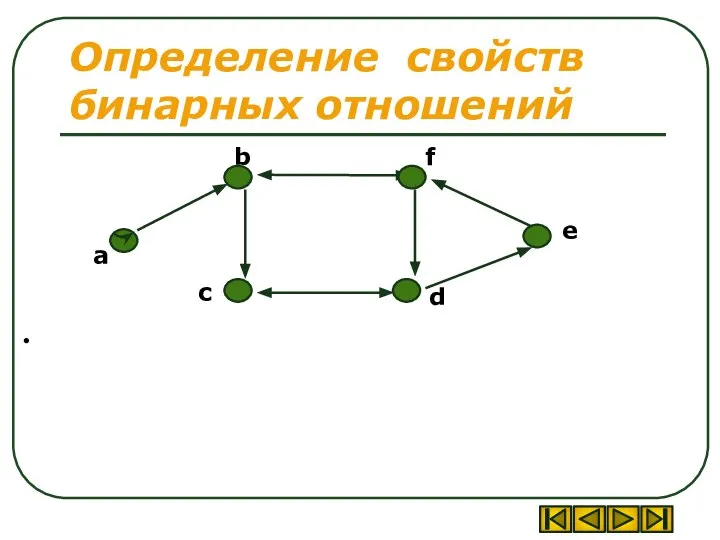
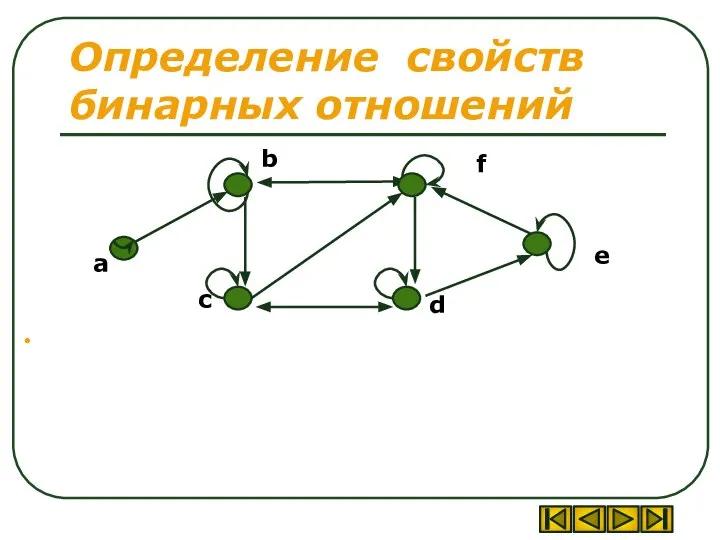
- 40. Определение свойств бинарных отношений
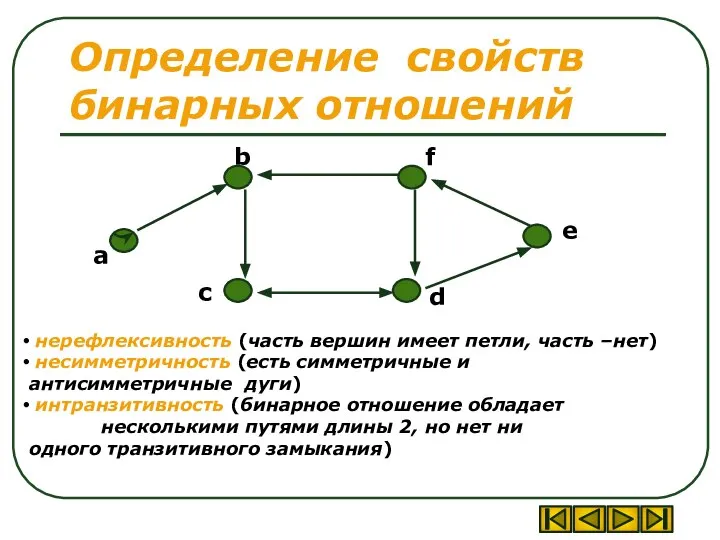
- 41. Определение свойств бинарных отношений нерефлексивность (часть вершин имеет петли, часть –нет) несимметричность (есть симметричные и антисимметричные
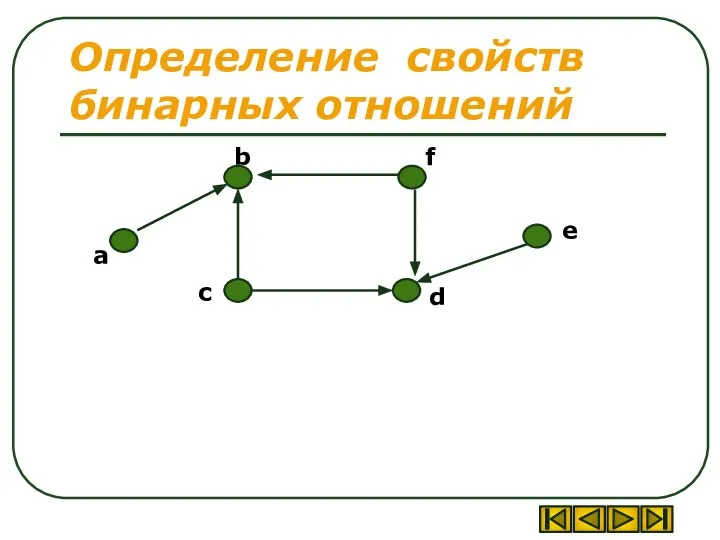
- 42. Определение свойств бинарных отношений
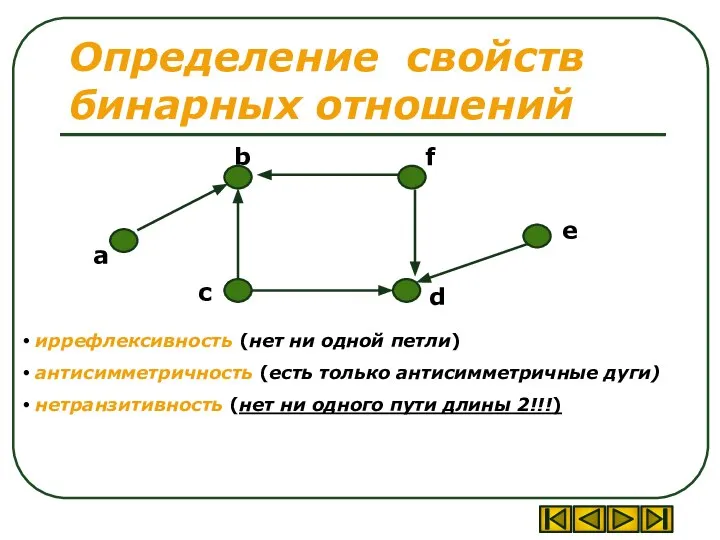
- 43. Определение свойств бинарных отношений иррефлексивность (нет ни одной петли) антисимметричность (есть только антисимметричные дуги) нетранзитивность (нет
- 44. Определение свойств бинарных отношений
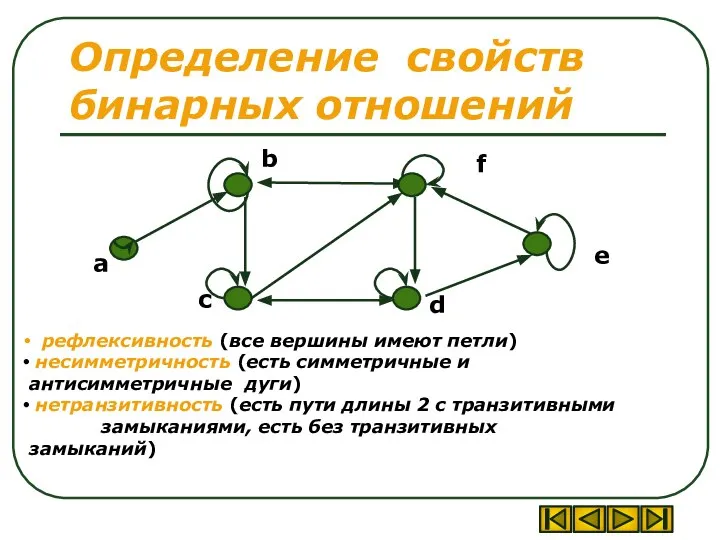
- 45. Определение свойств бинарных отношений рефлексивность (все вершины имеют петли) несимметричность (есть симметричные и антисимметричные дуги) нетранзитивность
- 46. Определение свойств бинарных отношений рефлексивность (число равно a самому себе, a=a ) несимметричность (нет ни одной
- 48. Скачать презентацию


























 Треугольники и их виды
Треугольники и их виды Десятичные дроби. Тест
Десятичные дроби. Тест Презентация на тему Пропорциональность величин (6 класс)
Презентация на тему Пропорциональность величин (6 класс)  Координатная плоскость. Задачи на движение
Координатная плоскость. Задачи на движение Приближённые значения чисел. Округление чисел
Приближённые значения чисел. Округление чисел Дроби. Числитель дроби
Дроби. Числитель дроби Решение задач. Многогранники. Тела вращения
Решение задач. Многогранники. Тела вращения Предел функции (часть 3)
Предел функции (часть 3) Математическая викторина. Блок 1 и 2
Математическая викторина. Блок 1 и 2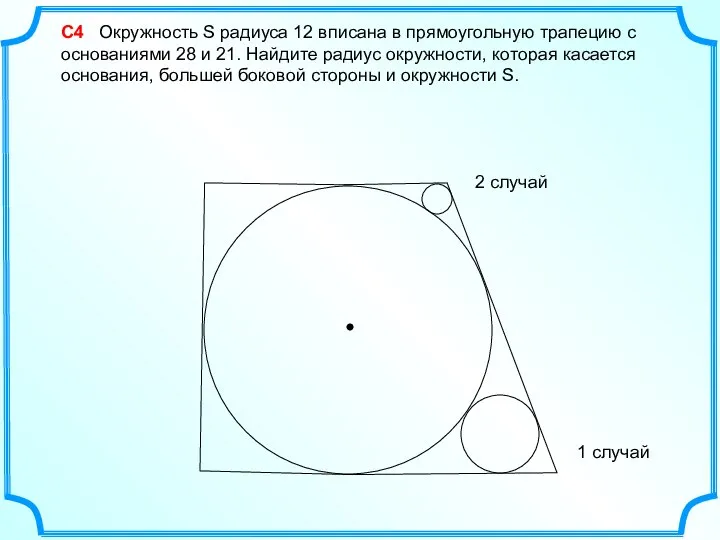 Вписанная окружность. Решение задач
Вписанная окружность. Решение задач Презентация на тему Логарифмическая функция
Презентация на тему Логарифмическая функция  Таблица сложения в пределах 20
Таблица сложения в пределах 20 Использование алгебры логики. Задача про карабли
Использование алгебры логики. Задача про карабли Решение уравнений. 7 класс
Решение уравнений. 7 класс Формулы приведения
Формулы приведения Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных
Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных Презентация на тему Определение арифметической прогрессии (9 класс)
Презентация на тему Определение арифметической прогрессии (9 класс)  Нестандартные уравнения
Нестандартные уравнения Деление десятичных дробей
Деление десятичных дробей Равнобедренный треугольник. Свойства равнобедренного треугольника
Равнобедренный треугольник. Свойства равнобедренного треугольника Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Вычисляем доли
Вычисляем доли Вектор. Равенство векторов
Вектор. Равенство векторов Десятичнвя дробь в виде смешанного числа
Десятичнвя дробь в виде смешанного числа Умножение дробей
Умножение дробей Свойства биссектрисы угла. Решение задач
Свойства биссектрисы угла. Решение задач Метод координат
Метод координат Оценки параметров распределения. Статистические оценки
Оценки параметров распределения. Статистические оценки