- Главная
- Математика
- Топология

Содержание
- 2. Общие сведения Лента Мёбиуса — поверхность с одной стороной и одним краем; пример объекта, изучаемого в
- 3. История Семь мостов Кёнигсберга — известная задача, решённая Эйлером и способствовавшая развитию топологии Раздел математики, который
- 4. Разделы топологии Общая топология Общая топология, или теоретико-множественная топология — раздел топологии, в котором изучается понятие
- 5. Литература Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. (Библиотечка «Квант», Вып.
- 7. Скачать презентацию
Слайд 2Общие сведения
Лента Мёбиуса — поверхность с одной стороной и одним краем; пример
Общие сведения
Лента Мёбиуса — поверхность с одной стороной и одним краем; пример

объекта, изучаемого в топологии
Топология (от др.-греч. τόπος — место и λόγος — слово, учение) — раздел математики, изучающий в самом общем виде явление непрерывности, в частности свойства пространств, которые остаются неизменными при непрерывных деформациях, например, связность, ориентируемость. В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов (например, расстояние между парой точек). Например, с точки зрения топологии, кружка и бублик (полноторий) неотличимы.
Весьма важными для топологии являются понятия гомеоморфизма и гомотопии. Грубо говоря, это типы деформации, происходящие без разрывов и склеиваний.
Топология (от др.-греч. τόπος — место и λόγος — слово, учение) — раздел математики, изучающий в самом общем виде явление непрерывности, в частности свойства пространств, которые остаются неизменными при непрерывных деформациях, например, связность, ориентируемость. В отличие от геометрии, в топологии не рассматриваются метрические свойства объектов (например, расстояние между парой точек). Например, с точки зрения топологии, кружка и бублик (полноторий) неотличимы.
Весьма важными для топологии являются понятия гомеоморфизма и гомотопии. Грубо говоря, это типы деформации, происходящие без разрывов и склеиваний.
Слайд 3История
Семь мостов Кёнигсберга — известная задача, решённая Эйлером и способствовавшая развитию топологии
Раздел
История
Семь мостов Кёнигсберга — известная задача, решённая Эйлером и способствовавшая развитию топологии
Раздел

математики, который мы теперь называем топологией, берет свое начало с изучения некоторых задач геометрии. Различные источники указывают на первые топологические по духу результаты в работах Лейбница и Эйлера, однако термин «топология» впервые появился в 1847 году в работе Листинга. Листинг определяет топологию так:
«Под топологией будем понимать учение о модальных отношениях пространственных образов, или о законах связности, взаимного положения и следования точек, линий, поверхностей, тел и их частей или их совокупности в пространстве, независимо от отношений мер и величин».
Когда топология еще только зарождалась (XVIII—XIX века), её называли геометрия размещения (лат. geometria situs) или анализ размещения (лат. analysis situs). Приблизительно с 1925 по 1975 годы топология являлась сильно развивающейся отраслью в математике.
Общая топология зародилась в конце XIX в. и оформилась в самостоятельную математическую дисциплину в начале XX в. Основополагающие работы принадлежат Хаусдорфу, Пуанкаре, Александрову, Урысону, Брауэру.
«Под топологией будем понимать учение о модальных отношениях пространственных образов, или о законах связности, взаимного положения и следования точек, линий, поверхностей, тел и их частей или их совокупности в пространстве, независимо от отношений мер и величин».
Когда топология еще только зарождалась (XVIII—XIX века), её называли геометрия размещения (лат. geometria situs) или анализ размещения (лат. analysis situs). Приблизительно с 1925 по 1975 годы топология являлась сильно развивающейся отраслью в математике.
Общая топология зародилась в конце XIX в. и оформилась в самостоятельную математическую дисциплину в начале XX в. Основополагающие работы принадлежат Хаусдорфу, Пуанкаре, Александрову, Урысону, Брауэру.
Слайд 4Разделы топологии
Общая топология
Общая топология, или теоретико-множественная топология — раздел топологии, в котором
Разделы топологии
Общая топология
Общая топология, или теоретико-множественная топология — раздел топологии, в котором

изучается понятие непрерывности в чистом виде. Здесь исследуются фундаментальные вопросы топологии, а также отдельные вопросы, такие как связность и компактность.
Алгебраическая топология
Алгебраическая топология — раздел, в котором происходит изучение непрерывности с использованием алгебраических объектов, вроде гомотопических групп и гомологий.
Дифференциальная топология
Дифференциальная топология — раздел, где главным образом изучаются гладкие многообразия с точностью до диффеоморфизма и их включения (размещения) в другие многообразия. Этот раздел включает в себя маломерную топологию, в том числе теорию узлов.
Вычислительная топология
Вычислительная топология — раздел, находящийся на пересечении топологии, вычислительной геометрии и теории вычислительной сложности. Занимается созданием эффективных алгоритмов для решения топологических проблем и применением топологических методов для решения алгоритмических проблем, возникающих в других областях науки.
Алгебраическая топология
Алгебраическая топология — раздел, в котором происходит изучение непрерывности с использованием алгебраических объектов, вроде гомотопических групп и гомологий.
Дифференциальная топология
Дифференциальная топология — раздел, где главным образом изучаются гладкие многообразия с точностью до диффеоморфизма и их включения (размещения) в другие многообразия. Этот раздел включает в себя маломерную топологию, в том числе теорию узлов.
Вычислительная топология
Вычислительная топология — раздел, находящийся на пересечении топологии, вычислительной геометрии и теории вычислительной сложности. Занимается созданием эффективных алгоритмов для решения топологических проблем и применением топологических методов для решения алгоритмических проблем, возникающих в других областях науки.
Слайд 5Литература
Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982.
Литература
Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982.

(Библиотечка «Квант», Вып. 21).
Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. (Библиотека студента-математика. Вып. 3).
Вербицкий М. Лекции и задачи по топологии. — 2009.
Виро О. Я., Иванов О. А., Харламов В. М., Нецветаев Н. Ю. Элементарная топология. — 2007.
Коснёвски Ч. Начальный курс алгебраической топологии. — М.: Мир, 1983.
Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс. — М.: Мир, 1972.
Милнор Дж., Сташеф Дж. Характеристические классы. — М.: Мир, 1979.
Прасолов В. В. Наглядная топология. — М.: МЦНМО, 1995.
Стюарт Я. Топология. // Квант, № 7, 1992.
Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. (Библиотека студента-математика. Вып. 3).
Вербицкий М. Лекции и задачи по топологии. — 2009.
Виро О. Я., Иванов О. А., Харламов В. М., Нецветаев Н. Ю. Элементарная топология. — 2007.
Коснёвски Ч. Начальный курс алгебраической топологии. — М.: Мир, 1983.
Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс. — М.: Мир, 1972.
Милнор Дж., Сташеф Дж. Характеристические классы. — М.: Мир, 1979.
Прасолов В. В. Наглядная топология. — М.: МЦНМО, 1995.
Стюарт Я. Топология. // Квант, № 7, 1992.
- Предыдущая
Проверка теста. Таблицы Многоугольники в окружающем нас мире
Многоугольники в окружающем нас мире Сложение и вычитание векторов
Сложение и вычитание векторов Найдите все значения параметра a,
Найдите все значения параметра a, Применение комбинаторики и бинома Ньютона в теории вероятности
Применение комбинаторики и бинома Ньютона в теории вероятности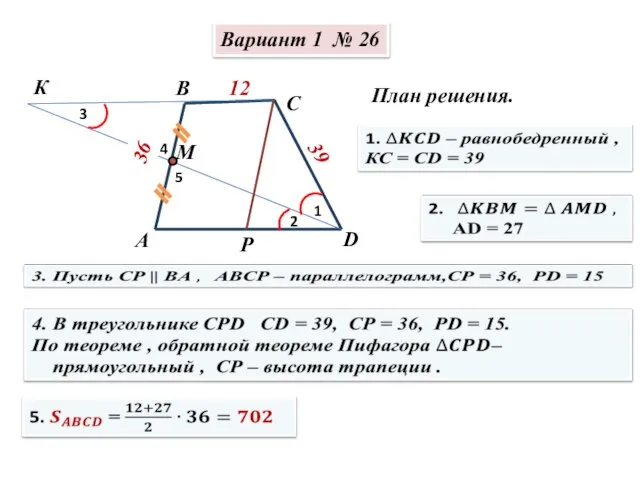 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Изучение конструкции в геометрии токарного резца
Изучение конструкции в геометрии токарного резца Биномиальное распределение
Биномиальное распределение Решение задания В8. Основные типы заданий
Решение задания В8. Основные типы заданий Суммы чисел
Суммы чисел Исследование функции на монотонность и экстремумы
Исследование функции на монотонность и экстремумы К разговору о пропорциях
К разговору о пропорциях Действия с дробями. Многогранники
Действия с дробями. Многогранники Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Преобразование иррациональных выражений
Преобразование иррациональных выражений Загадочное число
Загадочное число Решение задач на t°С воздуха и АД
Решение задач на t°С воздуха и АД Начала комбинаторики. Перестановки
Начала комбинаторики. Перестановки Презентация на тему Арифметическая прогрессия в древности
Презентация на тему Арифметическая прогрессия в древности  Элементы комбинаторики
Элементы комбинаторики Презентация на тему В царстве квадратных корней
Презентация на тему В царстве квадратных корней  Презентация на тему Определение подобных треугольников (8 класс)
Презентация на тему Определение подобных треугольников (8 класс)  Прямоугольник. Теоремы
Прямоугольник. Теоремы Основы эконометрического моделирования
Основы эконометрического моделирования Длиннее, короче (1 класс)
Длиннее, короче (1 класс) Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Умножение на три, треть числа Умножив три на единичку, Мы попадаем на страничку Из книги сказок для ребят Про ТРЕХ веселых порося
Умножение на три, треть числа Умножив три на единичку, Мы попадаем на страничку Из книги сказок для ребят Про ТРЕХ веселых порося Остановка Задачкино
Остановка Задачкино Возведение в степень. Диктант
Возведение в степень. Диктант