Содержание
- 2. Лекция 6
- 3. Условная вероятность
- 4. Пример Чему равна вероятность выпадения двух шестерок на двух игральных костях, если сумма выпавших очков четна?
- 5. Решение Введем события B={на обеих костях выпали шестерки} A={сумма очков четна}
- 6. Событию В благоприятствует всего один исход (6,6), поэтому P(B)=1/36 Событию А благоприятствует 18 исходов, поэтому P(A)=18/36=1/2
- 7. Так как пересечение AB=B, то условная вероятность
- 8. Теорема умножения вероятностей
- 9. Формула полной вероятности Пусть событие А может наступить при условии появления одного из несовместных событий которые
- 10. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий образующих
- 11. Пример Известно, что 5% мужчин и 0,25% женщин ─ дальтоники. Какова вероятность того, что наугад выбранный
- 12. Решение Рассмотрим два события A={выбран мужчина} B={выбрана женщина} Так как в группе одинаковое число мужчин и
- 13. Обозначим событие C={выбранный человек дальтоник} Условные вероятности P(C|A)=0,05 P(C|B)=0,0025 По формуле полной вероятности P(C)=0,05⋅0,5+0,0025⋅0,5=0,02625
- 14. Вероятность гипотез Формула Байеса Пусть событие А может наступить при условии появления одного из несовместных событий
- 15. Допустим, что произведено испытание, в результате которого появилось событие А.
- 16. Будем искать условные вероятности
- 18. Заменив здесь P(A) , получим
- 20. Полученные формулы называют формулами Байеса (по имени английского математика, который их вывел; опубликованы в 1764г.).
- 21. Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого
- 22. Пример Известно, что 5% мужчин и 0,25% женщин ─ дальтоники. Выбор производится из группы с равным
- 23. Решение A={выбран мужчина} B={выбрана женщина} C={выбранный человек дальтоник} Условные вероятности P(C|A)=0,05 P(C|B)=0,0025
- 24. Воспользовавшись формулой Байеса, находим
- 25. Задачи
- 26. Задача 1 Вероятности сбоя для различных элементов в компьютере относятся как 3:2:5. Вероятности обнаружения сбоя в
- 27. Решение A={сбой будет обнаружен} B1={сбой в устройстве 1} B2={сбой в устройстве 2} B3={сбой в устройстве 3}
- 28. Условные вероятности P(A|B1)=0,8; P(A|B2)=0,9; P(A|B3)=0,9 По формуле полной вероятности P(A)=0,3·0,8+0,2·0,9+0,5·0,9=0,87
- 29. Задача 2 У рыбака есть три любимых места рыбалка. Эти места он посещает с одинаковой вероятностью.
- 30. Решение A={рыбак вытащил рыбку} B1={рыбачил в первом месте} B2={рыбачил во втором месте} B3={рыбачил в третьем месте}
- 31. Условные вероятности P(A|B1)=1/3; P(A|B2)=1/2; P(A|B3)=1/4 По формуле Байеса
- 32. Задача 3 Путешественник может купить билет в одной из трех касс ж/д вокзала. Вероятность, что он
- 33. Решение A={купил билет} B1={обратился в кассу 1} B2={обратился в кассу 2} B3={обратился в кассу 3} Вероятности
- 34. Так как в условии задачи даны вероятности, что билетов в кассах уже нет, а путешественник купил
- 35. Искомая вероятность
- 36. Задача 4 Турист, заблудившись в лесу, вышел на полянку, от которой в разные стороны ведут 5
- 37. Решение A={турист вышел из леса} B1={выбрал дорогу 1} B2={выбрал дорогу 2} B3={выбрал дорогу 3} B4={выбрал дорогу
- 38. Дорог всего 5. Вероятности пойти по любой из пяти дорог одинаковы, то есть P(B1)=P(B2)=P(B3)=P(B4)=P(B5)=1/5 Условные вероятности
- 39. Имеем
- 40. Задача 5 Среди 25 экзаменационных билетов имеется 5 счастливых. Студенты подходят за билетами один за другим
- 41. Решение Обозначим события A={первый студент вытащил счастливый билет} B={второй студент вытащил счастливый билет} P(A)=5/25=1/5
- 42. Вероятность события B зависит от того, произошло или не произошло событие А. Поэтому P(B|A)=4/24 Если событие
- 43. Следовательно, вероятность P(B)=4/24⋅1/5+5/24⋅4/5=1/5, То есть совпадает с вероятностью события А.
- 44. Задача 6 Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания
- 45. Решение Обозначим события A1={на линию огня вызван 1-й стрелок} A2={на линию огня вызван 2-й стрелок} A3={на
- 46. Событие B={мишень не поражена} Условные вероятности этого события P(B|A1)=0,7⋅0,7=0,49 P(B|A2)=0,5⋅0,5=0,25 P(B|A3)=0,2⋅0,2==0,04
- 47. По формуле Байеса находим
- 48. Задача 7 В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20%
- 49. Решение Обозначим события B={куплена продукция высшего сорта} A1={продукция принадлежит 1-му предприятию} A2={продукция принадлежит 2-му предприятию} A3={продукция
- 50. По условию задачи P(A1)=0,2 P(A2)=0,3 P(A3)=0,5 Условные вероятности P(B|A1)=0,1 P(B|A2)=0,05 P(B|A3)=0,2 По формуле полной вероятности P(B)=0,2⋅0,1+0,3⋅0,05+0,5⋅0,2=0,135
- 51. Задача 8 Для сигнализации о том, что режим автоматической линии отклоняется от нормального, используется индикатор. Он
- 52. Решение Обозначим события A={от индикатора получен сигнал} B1={индикатор 1-го типа} B2={индикатор 2-го типа} B3={индикатор 3-го типа}
- 53. Условные вероятности P(A|B1)=1 P(A|B2)=0,75 P(A|B3)=0,4 Чтобы ответить на вопрос задачи, нужно найти вероятности P(B1|A), P(B2|A), P(B3|A)
- 54. По формуле полной вероятности найдем P(A)=0,2⋅1+0,3⋅0,75+0,5⋅0,4=0,625 Вероятность того, что сигнал будет получен от индикатора, принадлежащего 1-му
- 55. Вероятность, что сигнал будет поучен от индикатора 2-го типа Вероятность, что сигнал будет поучен от индикатора
- 56. Сравнив найденные вероятности, получаем ответ ─ вероятнее всего второму
- 57. Вопросы к лекции 6 Условная вероятность. Примеры Формула полной вероятности Формула Байеса
- 59. Скачать презентацию















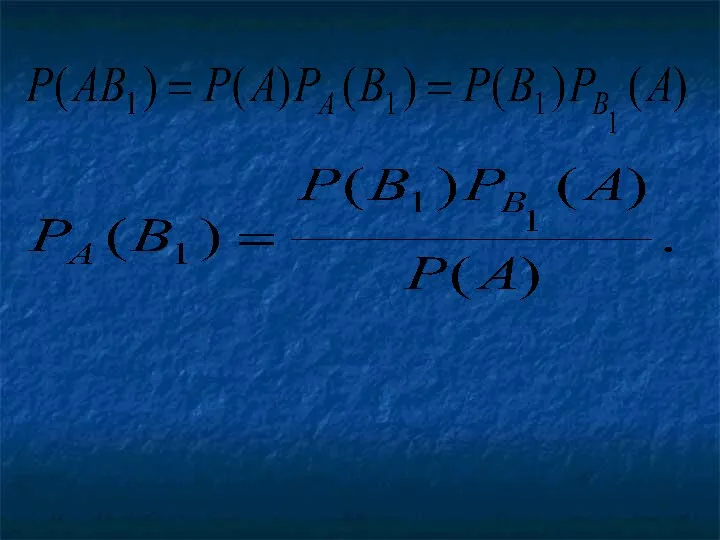

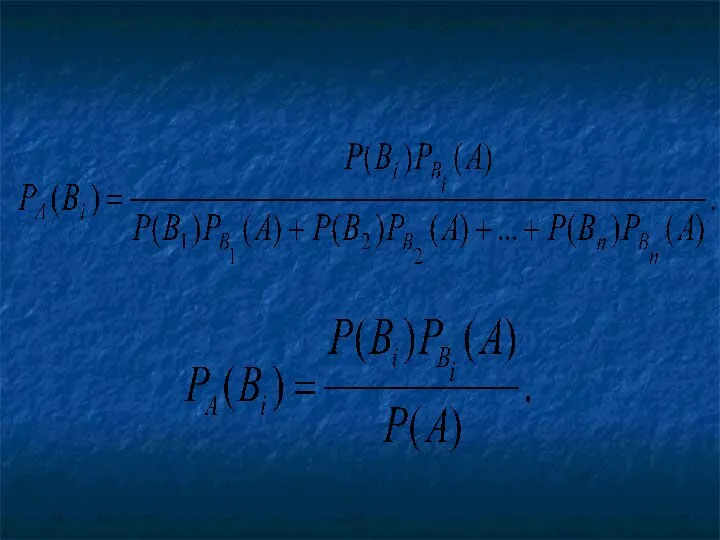















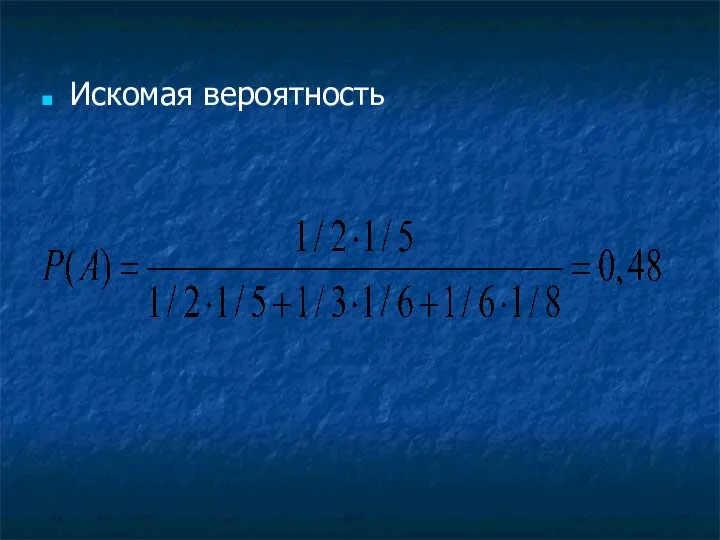






















 Определенный интеграл
Определенный интеграл Цилиндр. История возникновения
Цилиндр. История возникновения Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика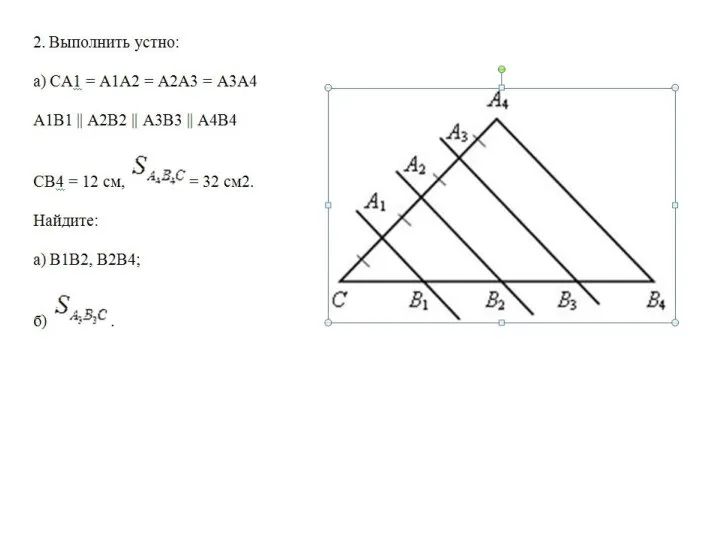 Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Приложения Определенного интеграла
Приложения Определенного интеграла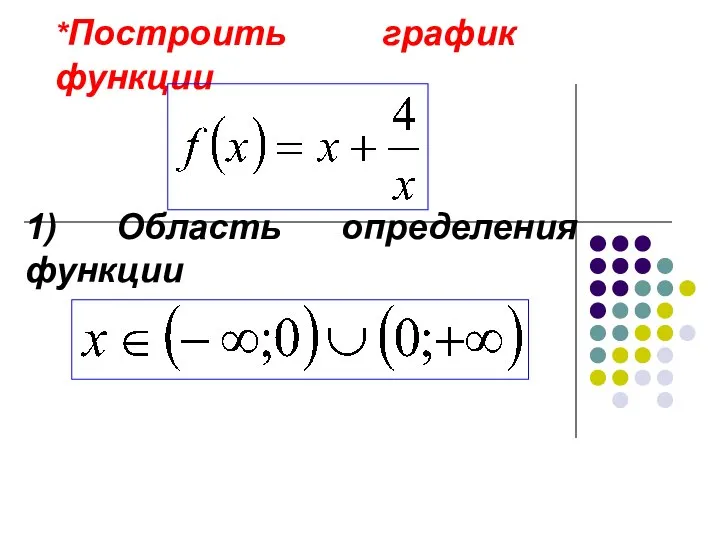 Построение графиков функций
Построение графиков функций Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Евклидовы пространства
Евклидовы пространства Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Параллельность плоскостей
Параллельность плоскостей Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения
Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Сложение десятичных дробей
Сложение десятичных дробей Рюкзак. Восстановление ответа
Рюкзак. Восстановление ответа Дискриминантный анализ Фишера с kernel trick
Дискриминантный анализ Фишера с kernel trick Степень числа
Степень числа Математическая викторина
Математическая викторина Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Как математика учит критическому мышлению
Как математика учит критическому мышлению Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Определение высоты дерева
Определение высоты дерева 12. Тэтраэдр
12. Тэтраэдр Знакомимся с многоугольниками
Знакомимся с многоугольниками Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч
Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч Делениес остатком
Делениес остатком