Применение производной к исследованию функций и построению графиков

Стационарные точки –внутренние точки области определения функции, в которых производная функции равна нулю
Критические точки – внутренние точки области определения функции, в которых функция непрерывна, но производная не существует
Точки перегиба – точка, разделяющая интервалы, в которых функция выпукла вниз и вверх
Точки
Точка экстремума – точка минимума и максимума функции
(лат. Extremum – «крайний»)

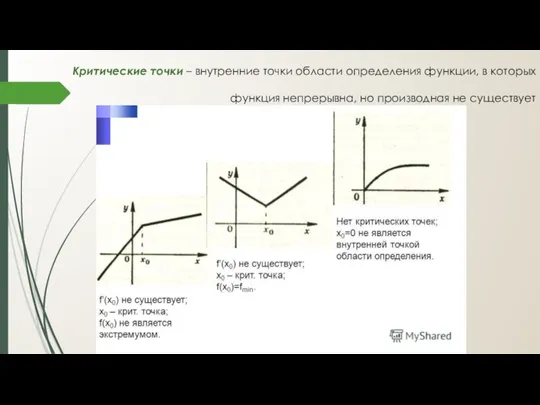
Критические точки – внутренние точки области определения функции, в которых функция непрерывна, но производная не существует

Исследование функции на монотонность
Исследовать функцию на монотонность, значит найти промежутки возрастания и убывания функции
Найдем производную данной функции
Из условия y’=0 найдем стационарные точки
Отметим найденные точки на числовой прямой
На полученных промежутках найдем знаки производной
Сделаем вывод о монотонности функции

Алгоритм нахождения наибольшего и наименьшего значения функции
Найдем производную данной функции
Из условия y’=0 найдем стационарные точки
Составим таблицу значений функции, где значение x – это концы отрезка и стационарные точки
Выберем из значений функции максимальное и минимальное значение

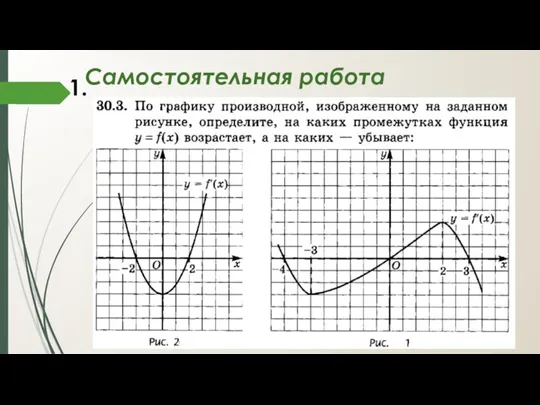
Самостоятельная работа
1.

2.
3.
4.