Содержание
- 2. ИЗМЕРЕНИЕ Измерение – это нахождение значения физической величины опытным путем с помощью специальных технических средств. Простейшим
- 3. Типы погрешностей Погрешностью Δx называют количественную характеристику неопределенности результата измерения x, оцененную экспериментатором на основе обработки
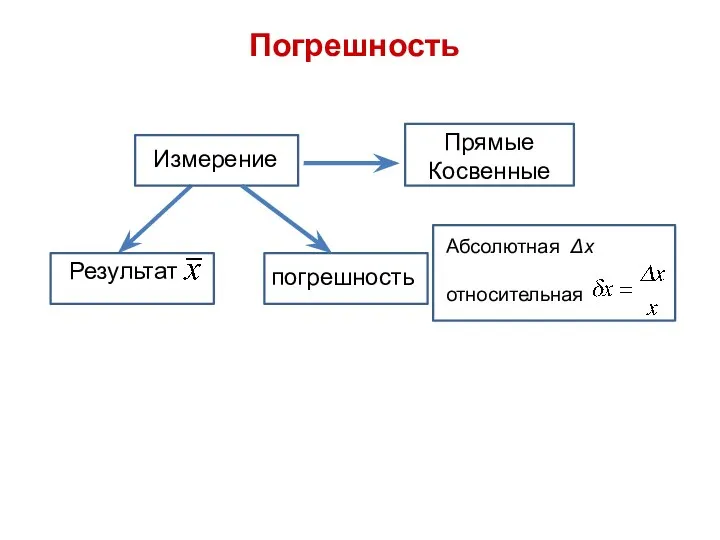
- 4. Погрешность
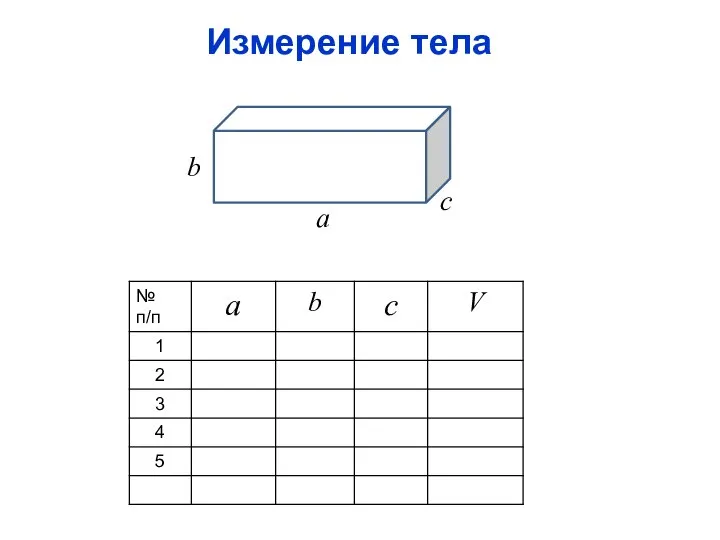
- 5. Измерение тела
- 6. Обработка результатов прямых измерений (Метод Стьюдента) 1. 2. Найти среднее квадратическое отклонение среднего значения 3. Задавшись
- 7. Обработка результатов прямых измерений (Метод Стьюдента) Такая запись означает, что истинный результат лежит в интервале Такой
- 8. Форма записи данных и правила округления при вычислениях 1. Число и его погрешность всегда записываются так,
- 9. Форма записи данных и правила округления ПРИМЕР: X = 56,473 Δx = 0,0278 ~ 0,03 →
- 10. ФИЗИКА Погрешность косвенных измерений
- 11. Вычисление погрешностей косвенных измерений Способ Аналогично прямым: II. Способ А) Если величина y определяется действием первой
- 12. Вычисление погрешностей косвенных измерений Пример: Определить погрешность измерения объема. V=abc
- 13. Пример: Определить погрешность измерения емкости С =С1 + С2 С±Δ С
- 15. Скачать презентацию










 Системы линейных алгебраических уравнений. Лекция 3а
Системы линейных алгебраических уравнений. Лекция 3а Умножение.Тест. 2 класс
Умножение.Тест. 2 класс Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Пропорция
Пропорция Состав числа 9
Состав числа 9 Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Пирамида. Элементы пирамиды
Пирамида. Элементы пирамиды Производная в географии
Производная в географии Решение линейных неравенств с одной переменной
Решение линейных неравенств с одной переменной Управление мыслительной деятельностью при решении математических заданий
Управление мыслительной деятельностью при решении математических заданий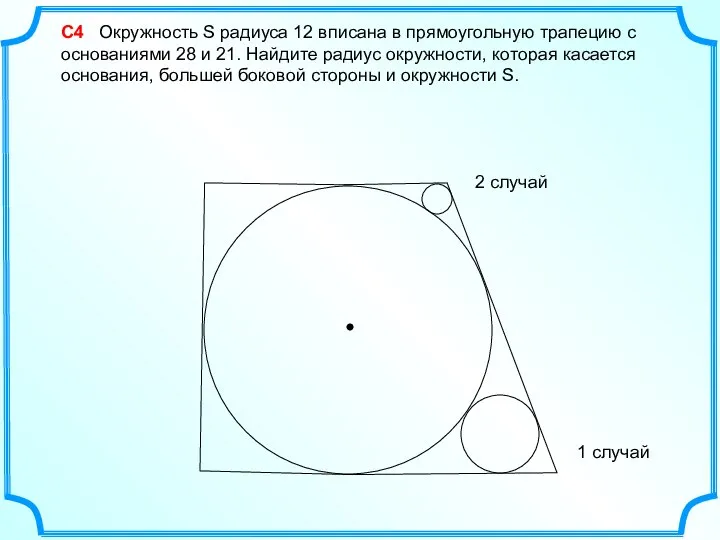 Вписанная окружность. Решение задач
Вписанная окружность. Решение задач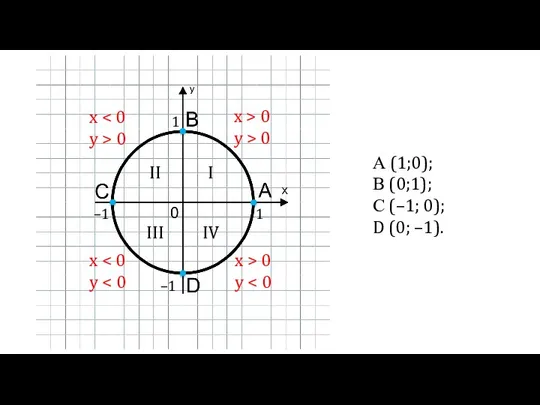 Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости Would you rather: thanksgiving edition
Would you rather: thanksgiving edition Метрология, основные понятия
Метрология, основные понятия Возведение в квадрат суммы и разности двух выражений. Тест
Возведение в квадрат суммы и разности двух выражений. Тест Решение задач
Решение задач Проверочная работа. 5 класс
Проверочная работа. 5 класс Степень.Симон Стевин
Степень.Симон Стевин Алгебра логики при решении практических задач
Алгебра логики при решении практических задач ЛP№1_Симплекс-метод окон
ЛP№1_Симплекс-метод окон Жили-были числа
Жили-были числа Сложение сил. Лабораторная работа №5
Сложение сил. Лабораторная работа №5 Нахождение площади
Нахождение площади Основные тригонометрические формулы
Основные тригонометрические формулы Рейтинг-контроль
Рейтинг-контроль Умножение и деление степеней
Умножение и деление степеней Сложение и вычитание вида +1 и -1
Сложение и вычитание вида +1 и -1 Нестандартный урок математики. Проведен учителем I категории Крутько В.И.
Нестандартный урок математики. Проведен учителем I категории Крутько В.И.