Содержание
- 2. откуда Задача 1. Решить уравнение Решение. Запишем уравнение в виде откуда Ответ. Задача 2. Решить уравнение
- 4. Решение.
- 5. Решение. Введем новую переменную Получаем квадратное уравнение: Находим корни квадратного уравнения: Возвращаемся к исходной переменной, получаем
- 6. Показательные неравенства Неравенства, в которых неизвестное содержится в показателе степени, называются показательными неравенствами. Алгоритм решения показательных
- 8. Получаем:
- 12. Логарифмические уравнения. При решении логарифмических уравнений обязательно учитывается ОДЗ (область допустимых значений)
- 13. Решение. 1. Находим ОДЗ: Приводим уравнение к такому виду, чтобы обе части уравнения представляли собой логарифмы
- 16. Решение логарифмических неравенств:
- 17. Решение. 1) Находим ОДЗ: Решаем систему неравенств: Графически находим общее решение:
- 20. Скачать презентацию

















 Математика и техника. Их связь и значение
Математика и техника. Их связь и значение Презентация на тему Что такое функция
Презентация на тему Что такое функция  МХСИ
МХСИ Переместительное свойство умножения
Переместительное свойство умножения Умножение на 1 и 0
Умножение на 1 и 0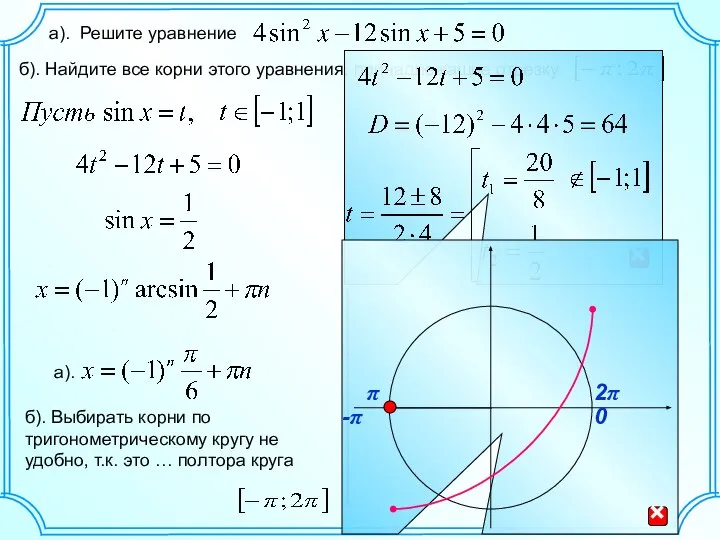 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Число и цифра 1. 1 класс
Число и цифра 1. 1 класс Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Презентация на тему Диаграммы (6 класс)
Презентация на тему Диаграммы (6 класс)  Образование чисел, которые больше 20
Образование чисел, которые больше 20 Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи Неполные квадратные уравнения
Неполные квадратные уравнения Геометрические портреты
Геометрические портреты Предмет математика. Счёт предметов. Один, два, три…
Предмет математика. Счёт предметов. Один, два, три… Комбинаторные задачи
Комбинаторные задачи Треугольник. Классификация треугольников
Треугольник. Классификация треугольников Задачи и примеры по математике
Задачи и примеры по математике Конкурс А ну-ка, математики!
Конкурс А ну-ка, математики! Устные упражнения по теме: корень п –ой степени
Устные упражнения по теме: корень п –ой степени Погрешности измерений
Погрешности измерений Первое знакомство с понятием вероятность. Урок 145
Первое знакомство с понятием вероятность. Урок 145 Числа и точки на прямой
Числа и точки на прямой Некоторые методические приемы для работы с детьми ЗПР на уроках математики
Некоторые методические приемы для работы с детьми ЗПР на уроках математики Зачем изучать математику?
Зачем изучать математику? Преобразование подобия
Преобразование подобия LP (1)
LP (1) Контрольная работа
Контрольная работа Подобные слагаемые
Подобные слагаемые