Производная и интеграл степенной функции с действительным показателем

Цели урока
11.3.1.9 - знать и применять правила нахождения производной степенной функции с действительным показателем;
11.3.1.10 - знать и применять правила нахождения интеграла степенной функции с действительным показателем

Производная степенной функции
Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.
Заметим, что в качестве степени может быть как натуральное число, то есть 1, 2, 3, ...; так и любое отрицательное число: - 1, - 2 и т.д., а также и любое дробное, например, 2,34; - 4,1 или .

Пример
Найти производную функции:
Решение
Искомая производная:
Находим производную степенной функции по формуле:
Ответ:

Интеграл степенной функции
Интеграл от степенной функции равен этой же функции в степени на единицу больше, деленной на эту же степень, плюс постоянная интегрирования.
Заметим, что в качестве степени может быть как натуральное число; так и любое отрицательное число, кроме (- 1), а также и любое дробное, например, 2,34; - 4,1 или .
Если n=-1, то

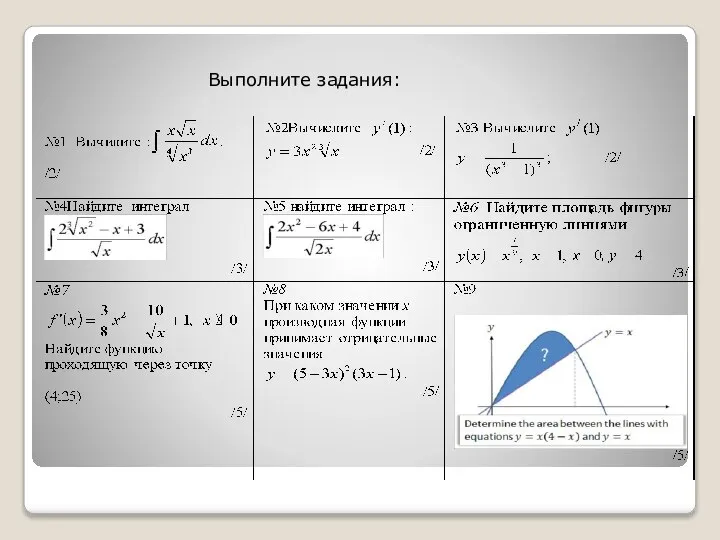
Упражнения
Заполните пропуски
Найдите интегралы функции

Выполните задания: