Содержание
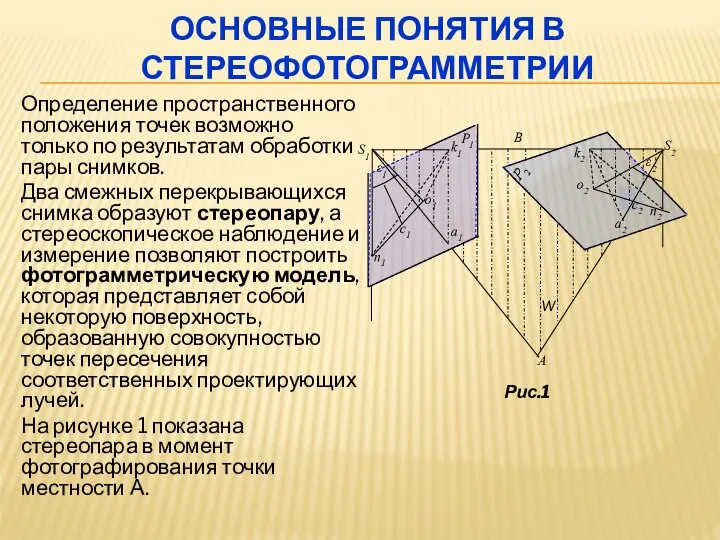
- 2. ОСНОВНЫЕ ПОНЯТИЯ В СТЕРЕОФОТОГРАММЕТРИИ Определение пространственного положения точек возможно только по результатам обработки пары снимков. Два
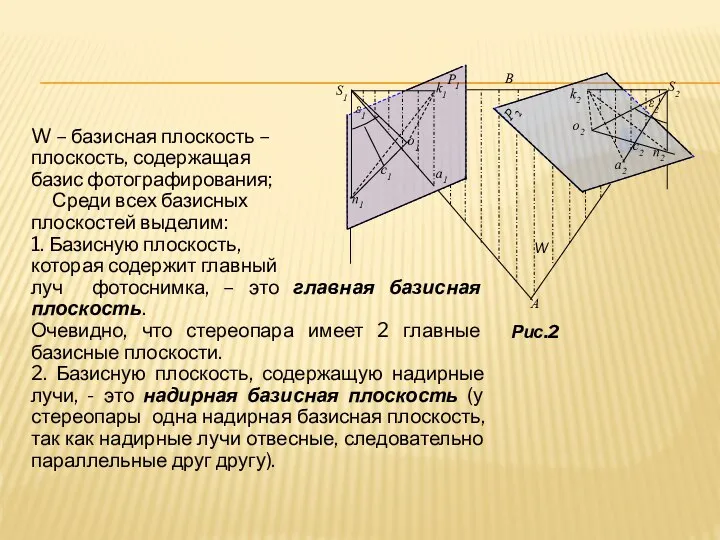
- 3. W – базисная плоскость – плоскость, содержащая базис фотографирования; Среди всех базисных плоскостей выделим: 1. Базисную
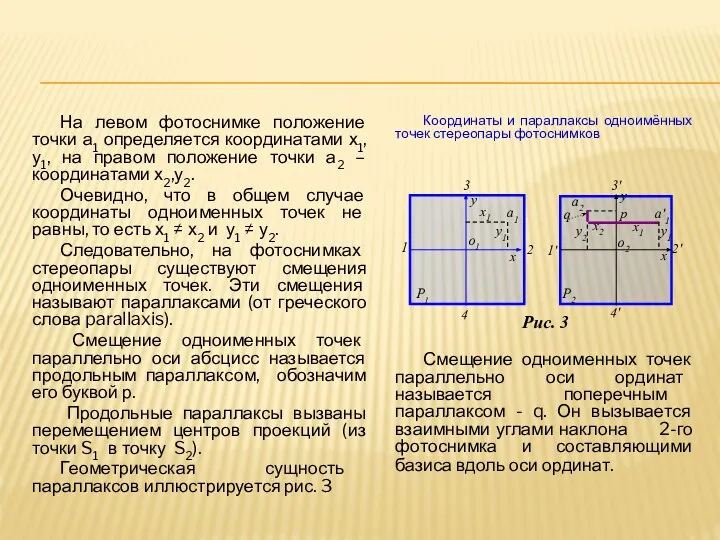
- 4. На левом фотоснимке положение точки а1 определяется координатами х1,у1, на правом положение точки а2 – координатами
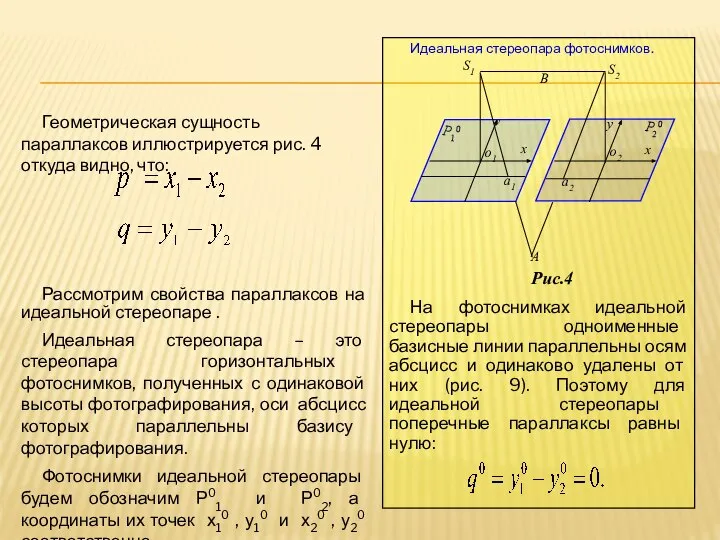
- 5. Геометрическая сущность параллаксов иллюстрируется рис. 4 откуда видно, что: Рассмотрим свойства параллаксов на идеальной стереопаре .
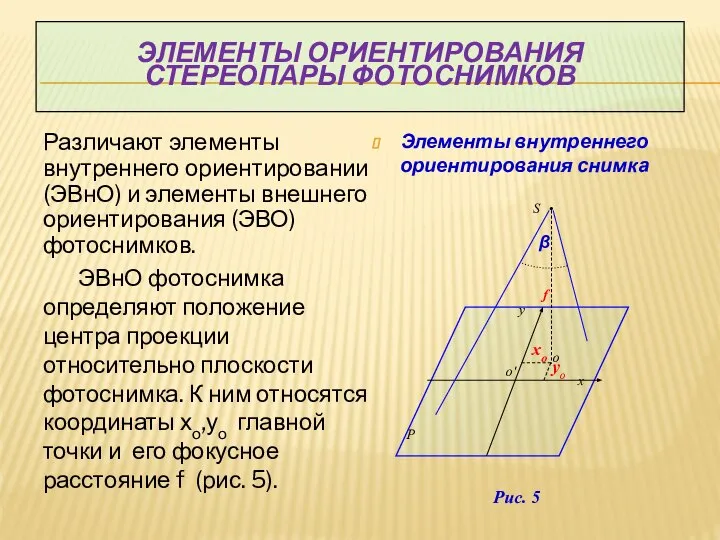
- 6. ЭЛЕМЕНТЫ ОРИЕНТИРОВАНИЯ СТЕРЕОПАРЫ ФОТОСНИМКОВ Различают элементы внутреннего ориентировании (ЭВнО) и элементы внешнего ориентирования (ЭВО) фотоснимков. ЭВнО
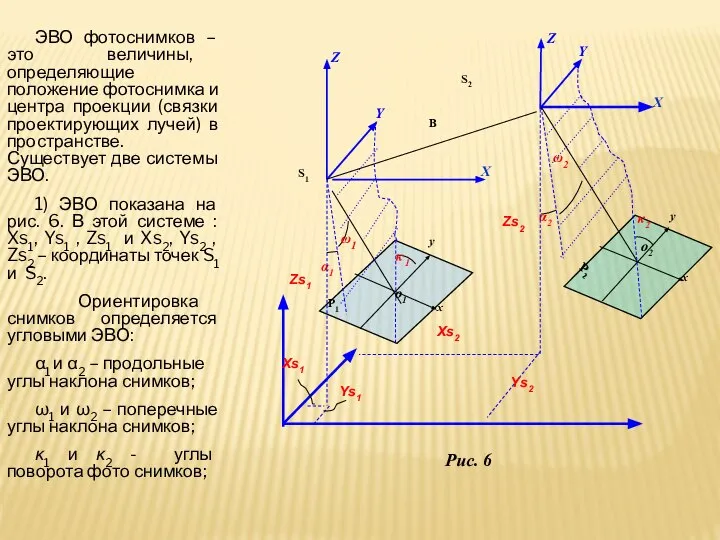
- 7. ЭВО фотоснимков – это величины, определяющие положение фотоснимка и центра проекции (связки проектирующих лучей) в пространстве.
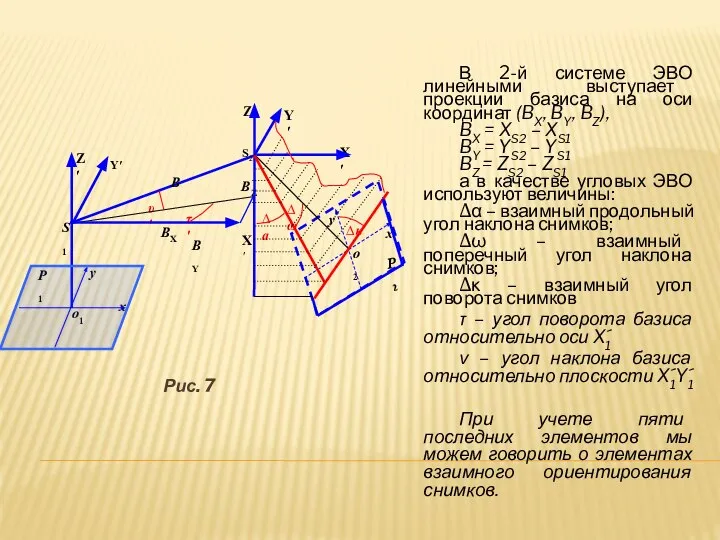
- 8. Рис. 7 В 2-й системе ЭВО линейными выступает проекции базиса на оси координат (BX, BY, BZ),
- 9. Таким образом, положение стереопары фотоснимков однозначно определяется пятнадцатью ЭО фотоснимков, которые составляют полную группу элементов ориентирования.
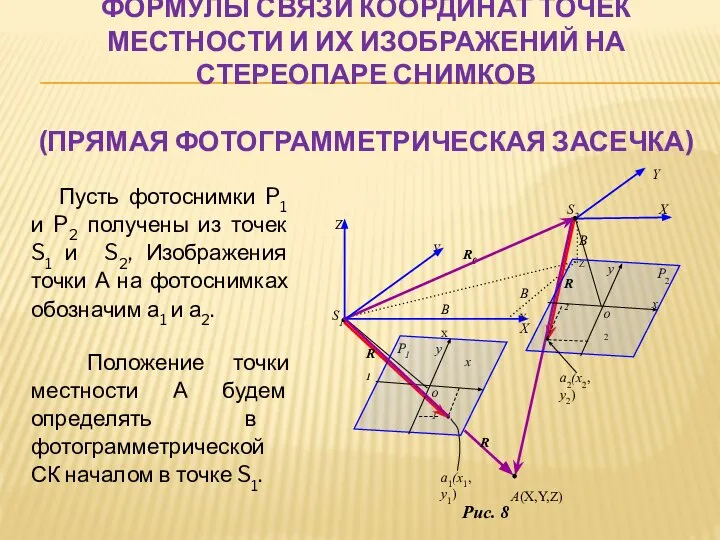
- 10. ФОРМУЛЫ СВЯЗИ КООРДИНАТ ТОЧЕК МЕСТНОСТИ И ИХ ИЗОБРАЖЕНИЙ НА СТЕРЕОПАРЕ СНИМКОВ (ПРЯМАЯ ФОТОГРАММЕТРИЧЕСКАЯ ЗАСЕЧКА) Пусть фотоснимки
- 11. Последовательность определения координат точки местности по стереопаре фотоснимков Измерим по фотоснимкам плоские прямоугольные координаты точек а1
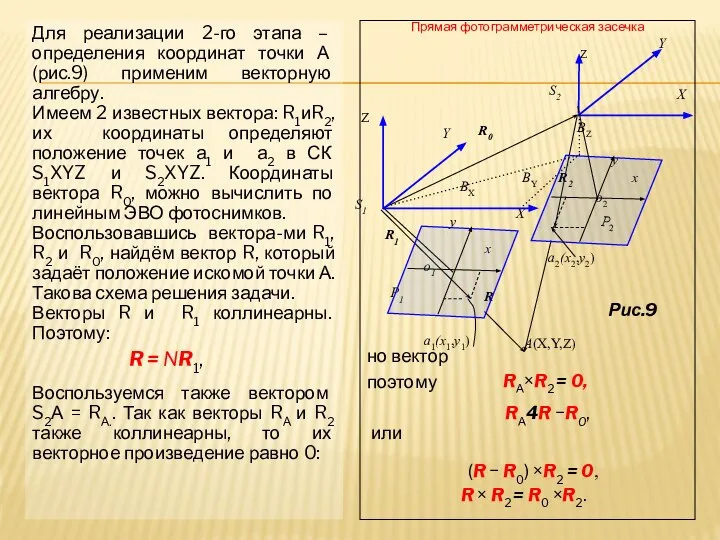
- 12. Для реализации 2-го этапа – определения координат точки А (рис.9) применим векторную алгебру. Имеем 2 известных
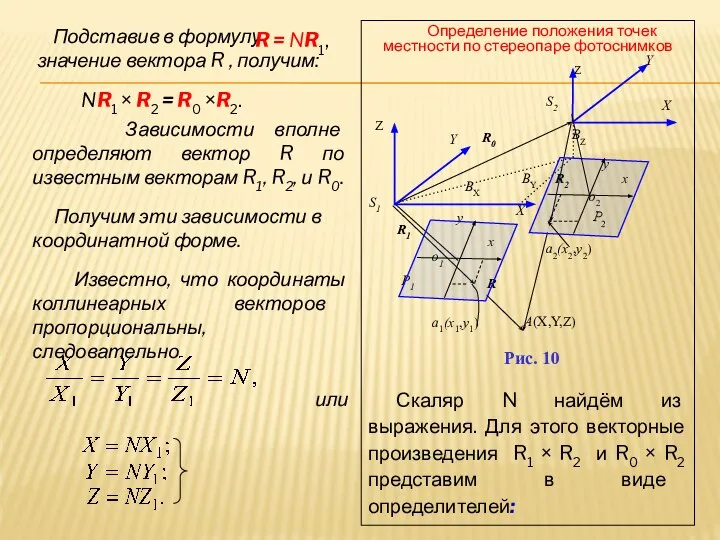
- 13. Подставив в формулу значение вектора R , получим: Зависимости вполне определяют вектор R по известным векторам
- 14. Дальше, если разложить определители по элементам первых строк и учесть что векторы R1 × R2 и
- 15. Из этих зависимостей следует, что по стереопаре можно определить не только плановые координаты, но и высоту
- 16. Зависимости между координатами точки местности и координатами её изображений на стереопаре фотоснимков описывают прямую фотограмметрическую засечку.
- 17. ФОРМУЛЫ СВЯЗИ КООРДИНАТ ТОЧЕК МЕСТНОСТИ И ИХ ИЗОБРАЖЕНИЙ НА СТЕРЕОПАРЕ СНИМКОВ ИДЕАЛЬНОГО СЛУЧАЯ СЪЕМКИ Наиболее просто
- 18. Подставив значения направляющих косинусов в формулы (3.21) и (3.22), получим зависимости, связывающие плоские и пространственные координаты
- 19. Значение скаляра N, с учётом того, что для идеальной стереопары составляющая базиса BX равна базису фотографирования
- 20. Заключение Формулы прямой фотограмметрической засечки свидетельствуют о том, что стереопара в отличие от одиночного фотоснимка позволяет
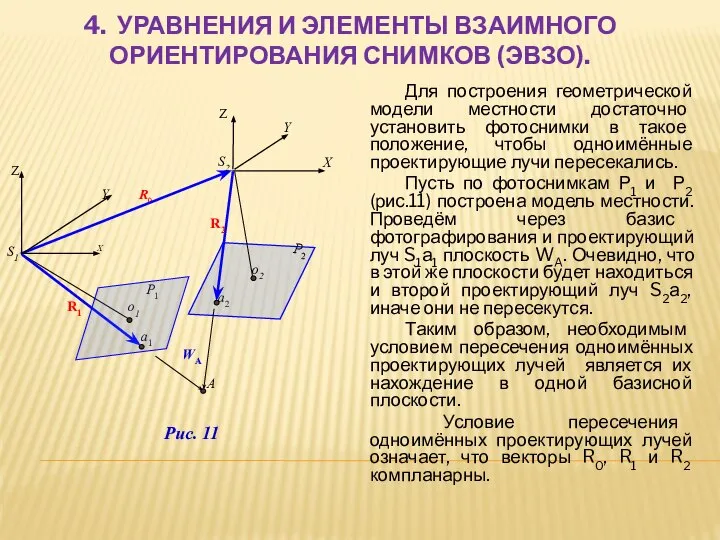
- 21. 4. УРАВНЕНИЯ И ЭЛЕМЕНТЫ ВЗАИМНОГО ОРИЕНТИРОВАНИЯ СНИМКОВ (ЭВЗО). Для построения геометрической модели местности достаточно установить фотоснимки
- 22. Условие компланарности трёх векторов выражается равенством нулю их скалярно-векторного произведения: где R0 (XS2, YS2, Z S2)
- 23. Следовательно, условие пересечения одноимённых проектирующих лучей связывает между собой только направления проектирующих лучей с направлением базиса.
- 24. Под взаимным ориентированием будем подразумевать установку фотоснимков стереопары в такое положение, при котором каждая пара одноимённых
- 25. Взаимное же положение фотоснимков, как в 1-м, так и во 2-м случаях характеризуется разностями их ЭВО:
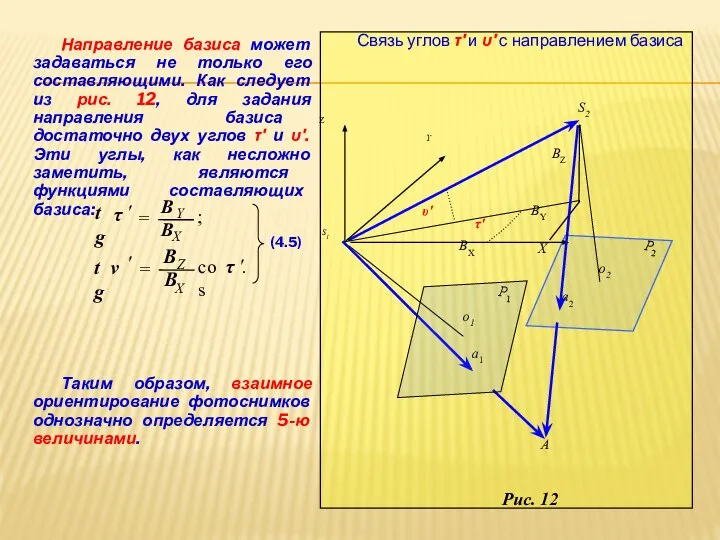
- 26. Направление базиса может задаваться не только его составляющими. Как следует из рис. 12, для задания направления
- 27. Величины, определяющие взаимное положение фотоснимков стереопары, при котором каждая пара одноимённых проектирующих лучей пересекается, называются элементами
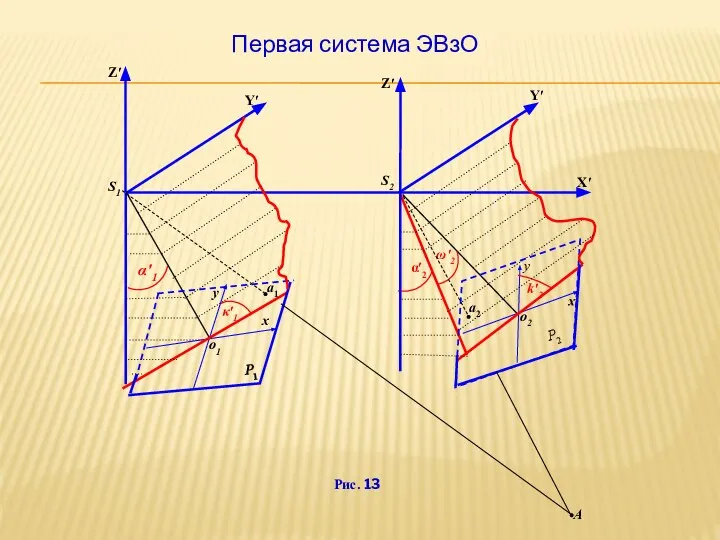
- 28. Первая система ЭВзО
- 29. 2-я группа ЭВзО определяется относительно СК с началом в точке S1, а оси X′ и Y′
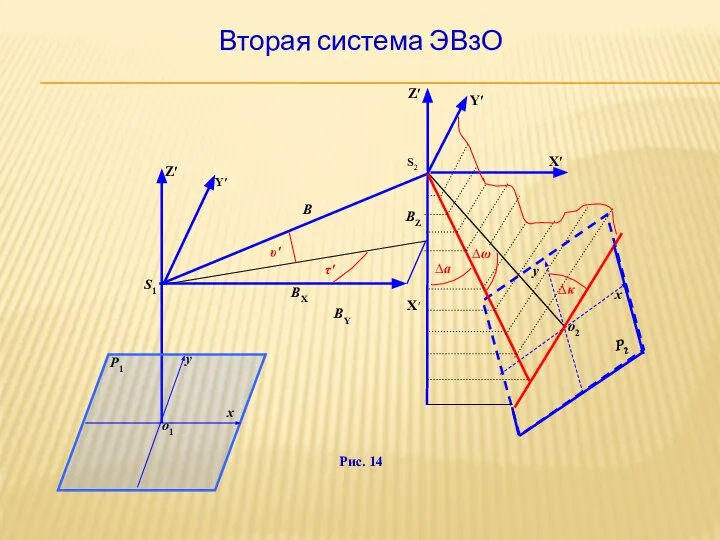
- 30. Вторая система ЭВзО Рис. 14
- 31. Для определения ЭВзО необходимо знать их связи с теми величинами, которые можно измерить по фотоснимкам. ЭВзО
- 32. Зависимости, связывающие ЭВзО с координатами одноимённых точек фотоснимков стереопары, принято называть уравнениями взаимного ориентирования. Вид уравнения
- 33. 1. Уравнения взаимного ориентирования фотоснимков 1-м способом а) Строгое уравнение ВзО Для ЭВзО первой системы XВ
- 34. В зависимости пространственные координаты одноимённых точек стереопары фсотоснимков, которые в соответствии с уравнениями равны: где a′1i,b′1i,c′1i
- 35. С учётом значений пространственных координат точек фотоснимков уравнение взаимного ориентирования примет вид: Уравнение взаимного ориентирования строгое,
- 36. б) Приближённое уравнение ВзО Направляющие косинусы для одиночного фотоснимка равны: Применительно к ЭВзО 1-й системе примут
- 37. В уравнениях ЭВзО связаны с координатами одноимённых точек и ЭВнО фотоснимков. Так как ЭВнО, как правило,
- 38. 2. Уравнения взаимного ориентирования фотоснимков вторым способом В соответствии с условием выбора системы координат для второй
- 39. Аналогично, как и для уравнения взаимного ориентирования 1-м способом, можно получить приближённую зависимость и для уравнения
- 40. Таким образом, вся необходимая информация для построения модели местности по стереопаре фотоснимков, содержится в самой стереопаре.
- 41. ОПРЕДЕЛЕНИЕ ЭВЗО СТЕРЕОПАРЫ ФОТОСНИМКОВ ПО ОПОРНЫМ ТОЧКАМ а) Определение ЭВзО первой системы. Теоретическую основу строгого способа
- 42. Для частных производных в зависимости примем следующие обозначения: Приближённое значение функции обозначим: Значение функции полученное после
- 43. а′1i,b′1i,с′1i – НК, вычисленные по ЭВзО α′1 и κ′1 левого фотоснимка стереопары; а′2i,b′2i,с′2i – НК, вычисленные
- 44. Б) СУЩНОСТЬ СТРОГОГО СПОСОБА ОПРЕДЕЛЕНИЯ ЭВЗО ВТОРОЙ СИСТЕМЫ Теоретическую основу строгого способа определения ЭВзО 2-й системы
- 45. Если разложить полученный определитель по элементам первой строки, то получим: В уравнении значения пространственных координат правого
- 46. Уравнение взаимного ориентирование 2-й системы Зависимость – это строгое уравнение взаимного ориентирования 2-м способом в развёрнутом
- 48. Скачать презентацию































 Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Повторение пройденного (1 класс)
Повторение пройденного (1 класс) Обратные тригонометрические функции
Обратные тригонометрические функции Օբյեկտ-կողմնորոշված ծրագրավորման լեզու
Օբյեկտ-կողմնորոշված ծրագրավորման լեզու Определенный интеграл. Формула Ньютона - Лейбница
Определенный интеграл. Формула Ньютона - Лейбница Уравнение окружности
Уравнение окружности 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Решение заданий олимпиады ПРОФИ 2017
Решение заданий олимпиады ПРОФИ 2017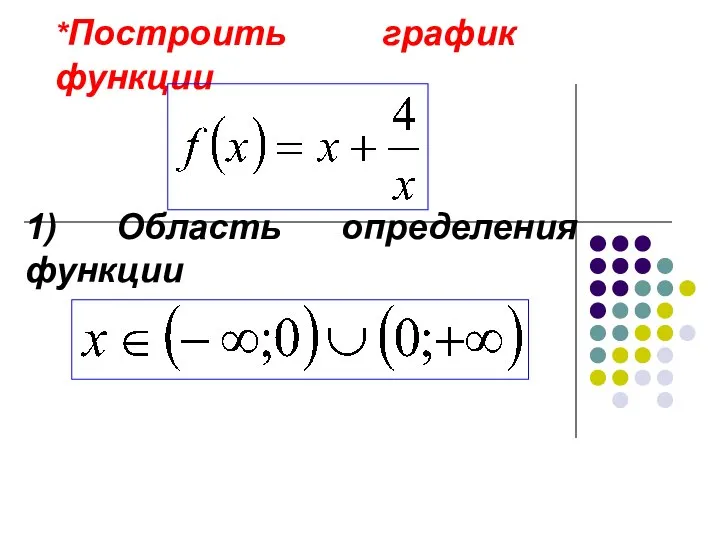 Построение графиков функций
Построение графиков функций Приемы вычислений для случаев вида 27+7
Приемы вычислений для случаев вида 27+7 Целостный подход. Производная функции y=f'(x)
Целостный подход. Производная функции y=f'(x)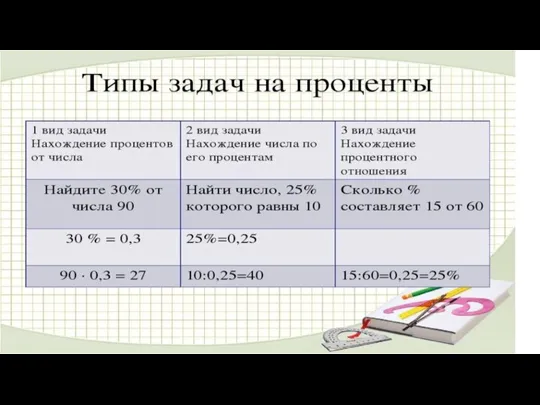 Задачи на проценты
Задачи на проценты теория вероятностей задачи
теория вероятностей задачи Кусочная функция
Кусочная функция Функция. Свойства функции. График функции
Функция. Свойства функции. График функции Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения с разделяющимися переменными Компоненты вычитания
Компоненты вычитания Движение
Движение Презентация на тему Математика и спорт (5 класс)
Презентация на тему Математика и спорт (5 класс)  Сравнение целых чисел
Сравнение целых чисел Уроки математики в Школе смешариков
Уроки математики в Школе смешариков Правильные многогранники
Правильные многогранники Решето эратосфена
Решето эратосфена Юный математик
Юный математик Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Роль математики в медицине
Роль математики в медицине