Слайд 21 семестр
Раздел 1. Введение в математический анализ.
Раздел 2. Дифференциальное исчисление функции одной

переменной.
Раздел 3. Применение производных к исследованию функций.
Раздел 4. Неопределенный интеграл.
Слайд 3Функции.
Предел функции.
Бесконечно малые и бесконечно большие функции.

Слайд 16Из определения предела функции по Гейне следует, что основные свойства предела последовательности

переносятся и на предел функции: единственность предела, арифметические свойства, возможность внесения знака предела под знак элементарной функции и т.д.
Для предела функции справедливо также все сказанное выше о неопределенностях
и их раскрытии.




























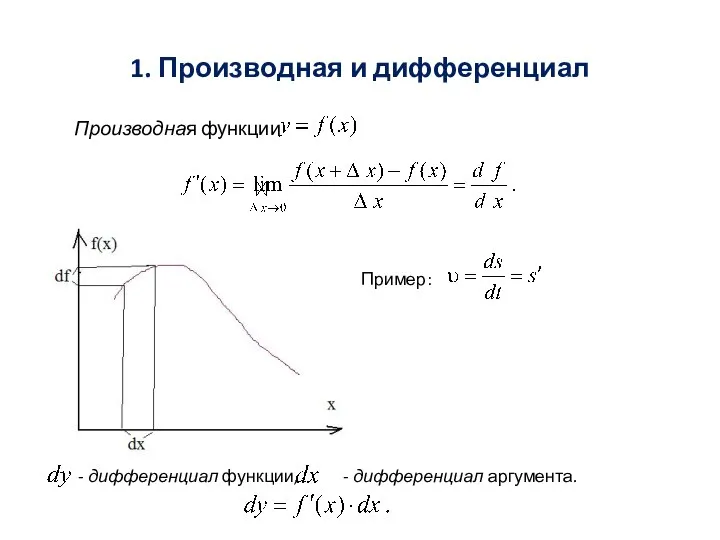 Производная и дифференциал
Производная и дифференциал Введение в геометрию
Введение в геометрию Построение графиков функций
Построение графиков функций Подготовка к ЕГЭ. Тестирование
Подготовка к ЕГЭ. Тестирование Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем Тригонометрические функции. Их свойства и график (1)
Тригонометрические функции. Их свойства и график (1) Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Открытый банк заданий по математике
Открытый банк заданий по математике Презентация на тему ЗАДАЧИ НА ДРОБИ
Презентация на тему ЗАДАЧИ НА ДРОБИ  Математический маятник
Математический маятник Элементы математической статистики
Элементы математической статистики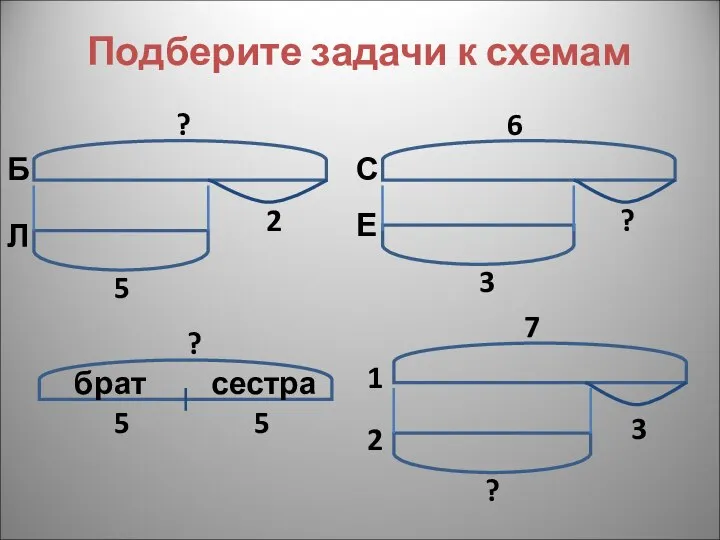 Единицы счёта
Единицы счёта Понятие о задачах математической статистики
Понятие о задачах математической статистики Презентация на тему Додекаэдр
Презентация на тему Додекаэдр  Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс Практическая работа
Практическая работа Векторы на плоскости. Понятие вектора. Равенство векторов
Векторы на плоскости. Понятие вектора. Равенство векторов Тренировка интеллекта. Задачи на логику
Тренировка интеллекта. Задачи на логику Построение графиков элементарных функций
Построение графиков элементарных функций Решение логарифмических уравнений
Решение логарифмических уравнений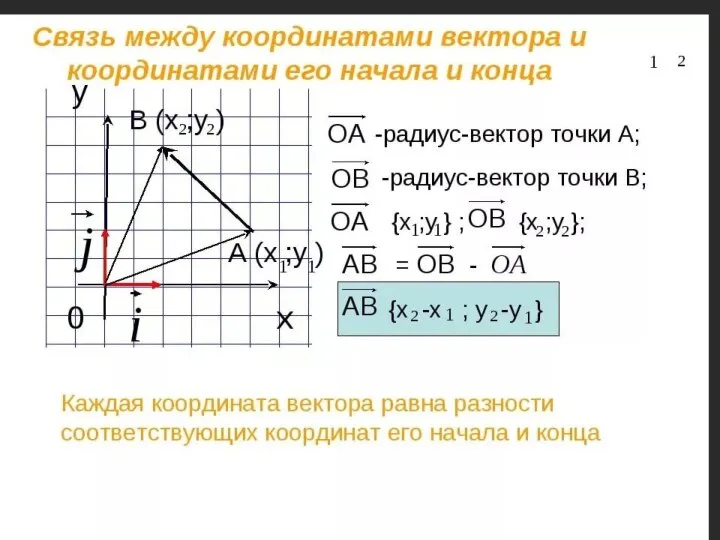 Векторы
Векторы Regresní a korelační analýza
Regresní a korelační analýza Угол
Угол Играем с лягушатами. Счет прямой и обратный
Играем с лягушатами. Счет прямой и обратный Эварист Галуа
Эварист Галуа Решение задач. 3 класс
Решение задач. 3 класс Случайные величины
Случайные величины Л 5 Функция одной переменной
Л 5 Функция одной переменной