Содержание
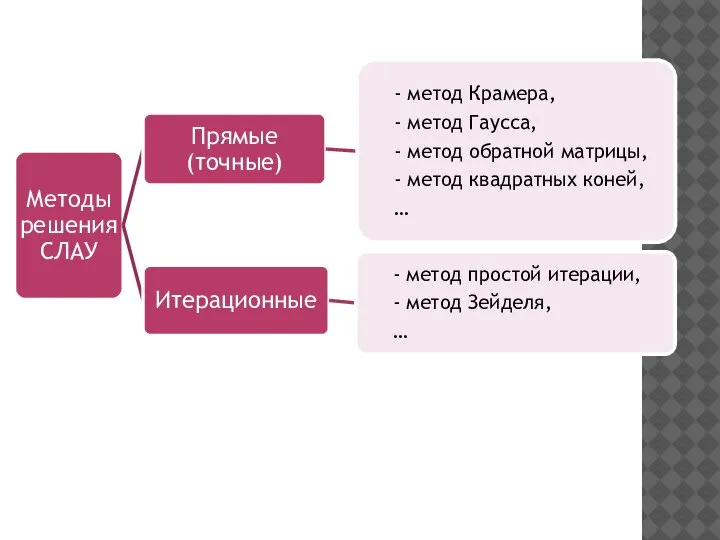
- 2. СИСТЕМА ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ) m – уравнений,n – неизвестных
- 3. СЛАУ В МАТРИЧНОМ ВИДЕ
- 4. ПРИМЕР ЗАДАЧ, РЕШЕНИЕ КОТОРЫХ СВОДИТСЯ К РЕШЕНИЮ СЛАУ
- 6. 2.1 ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
- 7. 2.1.1 МЕТОД ОБРАТНОЙ МАТРИЦЫ Решение: Дано:
- 8. 2.1.1 МЕТОД ОБРАТНОЙ МАТРИЦЫ Если m=n и detА≠0, то система имеет единственное решение. Вычисление обратной матрицы
- 9. 2.1.1 МЕТОД ОБРАТНОЙ МАТРИЦЫ Решение: Пример. Решить систему уравнений:
- 10. 2.1.1 МЕТОД ОБРАТНОЙ МАТРИЦЫ Решение:
- 11. 2.1.2 МЕТОД КРАМЕРА
- 12. 2.1.2 МЕТОД КРАМЕРА Решение: Пример. Решить систему уравнений:
- 13. 2.1.2 МЕТОД КРАМЕРА Решение:
- 14. 2.1.2 МЕТОД КРАМЕРА Решение:
- 15. 2.1.2 МЕТОД КРАМЕРА Решение:
- 16. 2.1.2 МЕТОД КРАМЕРА Решение:
- 17. 2.1.2 МЕТОД КРАМЕРА Решение:
- 18. 2.1.2 МЕТОД КРАМЕРА Решение:
- 19. 2.1.2 МЕТОД КРАМЕРА Решение:
- 20. 2.1.2 МЕТОД КРАМЕРА Пример: detA≠0, при больших n вычисление определителей трудоемко.
- 21. 2.1.3 МЕТОД ГАУССА алгоритм последовательного исключения неизвестных. Прямой ход:
- 22. 2.1.3 МЕТОД ГАУССА алгоритм последовательного исключения неизвестных. Прямой ход:
- 23. 2.1.3 МЕТОД ГАУССА алгоритм последовательного исключения неизвестных. Прямой ход:
- 24. 2.1.3 МЕТОД ГАУССА алгоритм последовательного исключения неизвестных. Прямой ход:
- 25. 2.1.3 МЕТОД ГАУССА Решение: Пример. Решить систему уравнений:
- 26. 2.1.3 МЕТОД ГАУССА Решение:
- 27. 2.1.3 МЕТОД ГАУССА Решение:
- 28. 2.1.3 МЕТОД ГАУССА Решение:
- 29. 2.1.3 МЕТОД ГАУССА Решение:
- 30. 2.1.3 МЕТОД ГАУССА Решение:
- 31. 2.1.3 МЕТОД ГАУССА алгоритм последовательного исключения неизвестных. Обратный ход:
- 32. 2.1.3 МЕТОД ГАУССА Решение:
- 33. 2.1.3 МЕТОД ГАУССА Решение:
- 34. 2.1.3 МЕТОД ГАУССА Решение:
- 35. 2.1.3 МЕТОД ГАУССА Решение:
- 36. 2.1.3 МЕТОД ГАУССА Необходимое и достаточное условие применимости: ведущие элементы ≠0
- 37. 2.1.4 МЕТОД ГЛАВНЫХ ЭЛЕМЕНТОВ За ведущий элемент выбирается наибольший по модулю и не принадлежащий столбцу свободных
- 38. 2.1.4 МЕТОД ГЛАВНЫХ ЭЛЕМЕНТОВ Применим, если det A≠0
- 39. 2.1.5 МЕТОД КВАДРАТНЫХ КОРНЕЙ Дано: Решение: ,
- 40. 2.1.5 МЕТОД КВАДРАТНЫХ КОРНЕЙ Дано: Решение: , Тогда
- 42. 2.1.5 МЕТОД КВАДРАТНЫХ КОРНЕЙ
- 44. 2.1.5 МЕТОД КВАДРАТНЫХ КОРНЕЙ
- 45. 2.1.5 МЕТОД КВАДРАТНЫХ КОРНЕЙ Решение: Пример. Решить систему уравнений:
- 46. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Дано: где А – квадратная матрица. Решение: нижняя треугольная матрица верхняя
- 47. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Дано: где А – квадратная матрица. Решение: Тогда нижняя треугольная матрица
- 48. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Дано: где А – квадратная матрица. Решение: Тогда нижняя треугольная матрица
- 49. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО)
- 50. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО)
- 51. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО)
- 52. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО)
- 53. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО)
- 54. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО)
- 55. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Решение: Пример. Решить систему уравнений:
- 56. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Решение:
- 57. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Решение:
- 58. 2.1.6 МЕТОД LU-РАЗЛОЖЕНИЯ (СХЕМА ХАЛЕЦКОГО) Решение:
- 59. 2.2 ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
- 60. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Дано: где А –матрица с ненулевыми диагональными коэффициентами. Решение: 1. Приведем систему
- 61. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Решение: Приведем систему к виду (*): Пример. Решить систему уравнений:
- 62. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Решение: Строим последовательные приближения:
- 63. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Если требуется точность m верных десятичных знаков, то: 1) вычисления ведем с
- 64. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Если требуется точность m верных десятичных знаков, то: 1) вычисления ведем с
- 66. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ . Процесс хорошо сходится , если элементы матрицы малы по абсолютной величине.
- 67. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ
- 68. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ . Процесс хорошо сходится , если элементы матрицы малы по абсолютной величине.
- 69. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Теорема. Процесс итерации для приведенной СЛАУ сходится к единственному ее решению, если
- 70. 2.2.1 МЕТОД ПРОСТОЙ ИТЕРАЦИИ Следствие. Процесс итерации для приведенной СЛАУ сходится к единственному ее решению, если
- 71. 2.2.2 МЕТОД ЗЕЙДЕЛЯ Дано: Решение: 1. Выбираем начальное приближение 2. Строим последовательные приближения c учетом уже
- 72. 2.2.2 МЕТОД ЗЕЙДЕЛЯ Пример: Решение: 1. Выбираем начальное приближение 2. Строим последовательные приближения: и т.д. .
- 74. Скачать презентацию










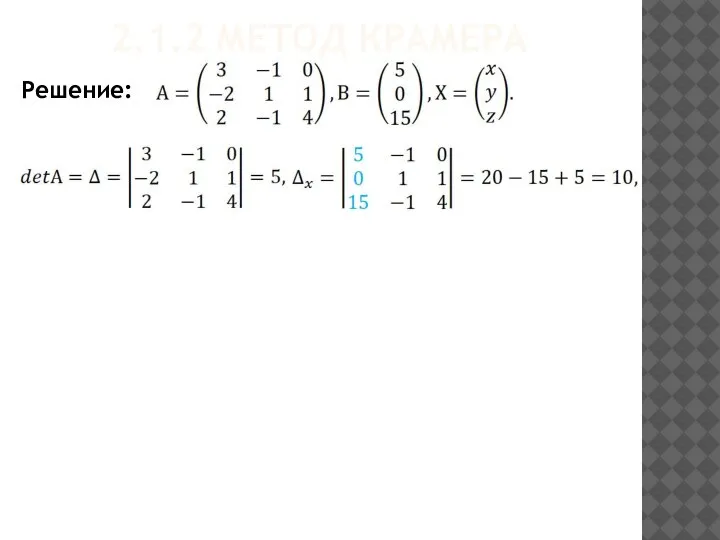












































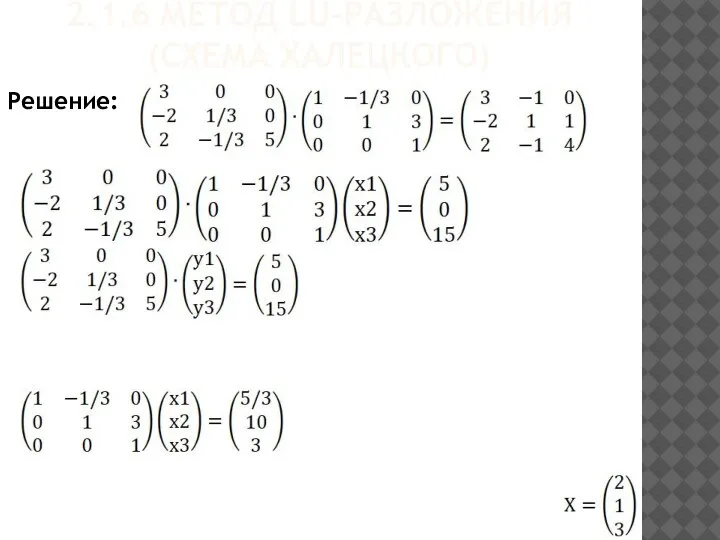














 Методика проверки и оценки алгебраических заданий повышенного уровня сложности
Методика проверки и оценки алгебраических заданий повышенного уровня сложности Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Применение производной к исследованию функций и построению графиков
Применение производной к исследованию функций и построению графиков Вырезаем квадрат
Вырезаем квадрат Расстояния. Подготовка к ЕГЭ по математике 2019
Расстояния. Подготовка к ЕГЭ по математике 2019 Значение переменных верного равенства. Корни уравнений
Значение переменных верного равенства. Корни уравнений Осевая и центральная симметрия
Осевая и центральная симметрия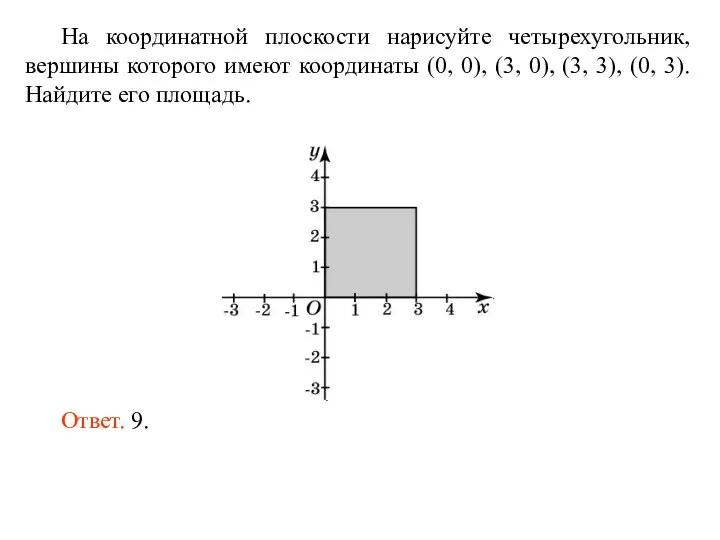 Площадь фигур
Площадь фигур Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов
Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов Марафон. Вопросы
Марафон. Вопросы Тела вращения. Конус
Тела вращения. Конус Медианы, биссектрисы и высота треугольника
Медианы, биссектрисы и высота треугольника Математика для детей (тест)
Математика для детей (тест) 3 класс. Разминка
3 класс. Разминка I признак подобия треугольников
I признак подобия треугольников Математика. 1 класс
Математика. 1 класс Lektsia-2-russ
Lektsia-2-russ Методика решения качественных и количественных задач
Методика решения качественных и количественных задач Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Построение сечений. Задачи
Построение сечений. Задачи Структура ОГЭ 2020 по математика
Структура ОГЭ 2020 по математика Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Число и цифра (старшая группа)
Число и цифра (старшая группа) Наука статистика
Наука статистика История возникновения числа ПИ
История возникновения числа ПИ Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)