Слайд 2Пусть задан произвольный n-мерный массив
Адрес произвольного элемента:

Слайд 3Величина Dm:
при отображении строками :
при отображении столбцами :

Слайд 5D3=1
D2=(5-1+1)*1=5
D1=(6-4+1)*5=15
2*(2*15+4*5+1*1)
MATR(2:3,4:6,1:5)

Слайд 6Пусть начальный адрес массива MATR=1000.
Тогда его элемент с индексами 2, 5, 4

будет располагаться по адресу :
ADDR(MATR(2,5,4))=ADDR(MATR(2,4,1))-
102+30*2+10*5+2*4=1000-102+118=1016.
Слайд 8Сложение разреженных векторов с использованием расширенного вещественного накопителя

Слайд 9Сложение разреженных векторов с использованием расширенного вещественного накопителя

Слайд 10Сложение разреженных векторов с использованием расширенного целого массива указателей
Скалярное умножение двух

разреженных векторов с использованием массива указателей
Слайд 11Диагональная схема хранения ленточных матриц
Здесь β - полуширина, а 2β+1 – ширина

ленты.
Лентой матрицы А называется множество элементов, для которых ⎪i-j⎪≤β.
Верхняя полулента состоит из элементов, находящихся в верхней части ленты, т.е. таких, что 0Массив имеет размеры n*(β+1).
Слайд 12Диагональная схема хранения ленточных матриц

Слайд 13Профильная схема хранения симметричных матриц
Для каждой строки i симметричной матрицы А

положим
Схема Дженнингса
Слайд 14Профильная схема хранения симметричных матриц
Оболочка матрицы А – это множество элементов ,

для которых
В строке i оболочке принадлежат все элементы со столбцовыми индексами от до i-1, всего элементов.
Диагональные элементы не входят в оболочку. Профиль матрицы А определяется как число элементов в оболочке:
Слайд 15Профильная схема хранения симметричных матриц
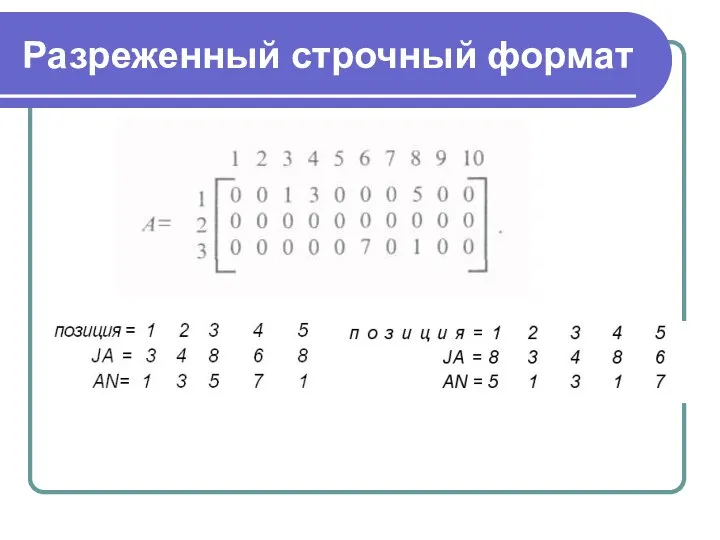
Позиция = 1 2 3 4 5 6 7

8 9 10 11 12 13 14
AN = 1 2 8 3 9 0 4 10 5 11 6 12 0 7
IA = 1 2 4 7 9 11 14
Слайд 16Связанные схемы разреженного хранения
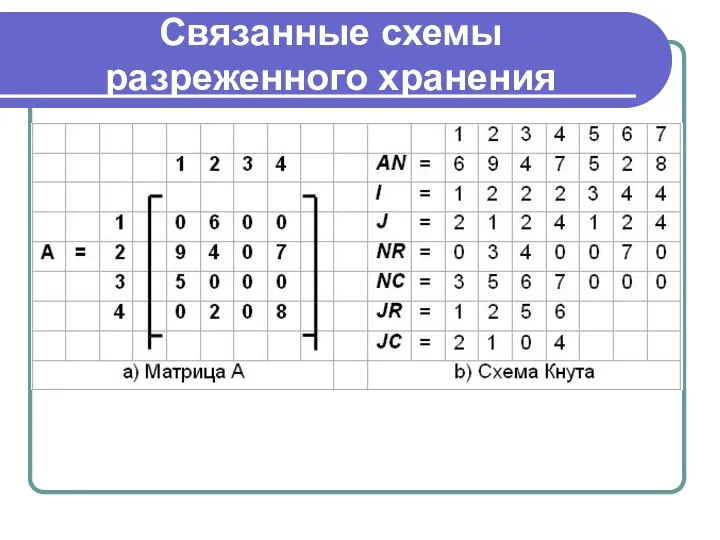
Слайд 17Связанные схемы разреженного хранения
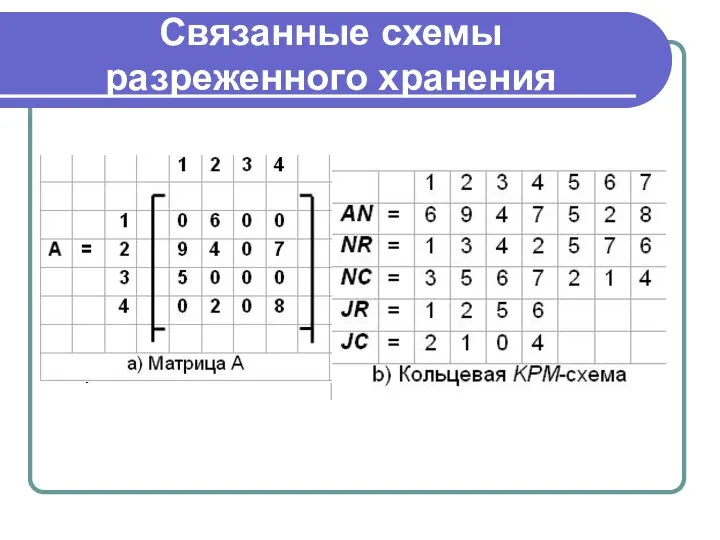
Слайд 18Связанные схемы разреженного хранения
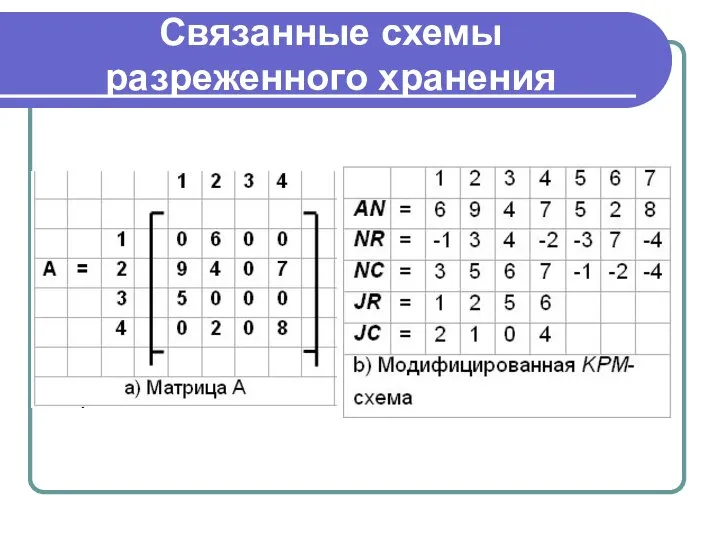
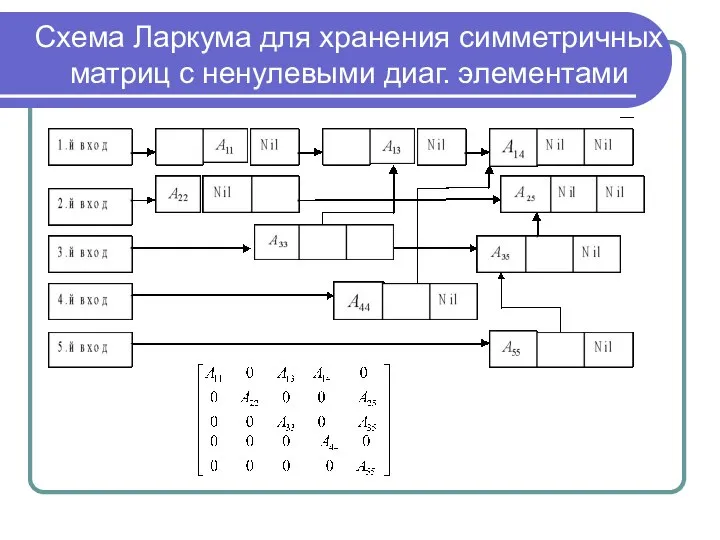
Слайд 19Схема Ларкума для хранения симметричных матриц с ненулевыми диаг. элементами

Слайд 20Схема Ларкума для хранения симметричных матриц с ненулевыми диаг. элементами
Слайд 21ДАННЫЕ ДИНАМИЧЕСКОЙ СТРУКТУРЫ
Списком называется линейно-упорядоченная последовательность элементов данных Е(1), Е(2),..., Е(n)
последовательный список

- последовательное расположение элементов списка
динамически связанный список - упорядоченность элементов задается с помощью специальных указателей
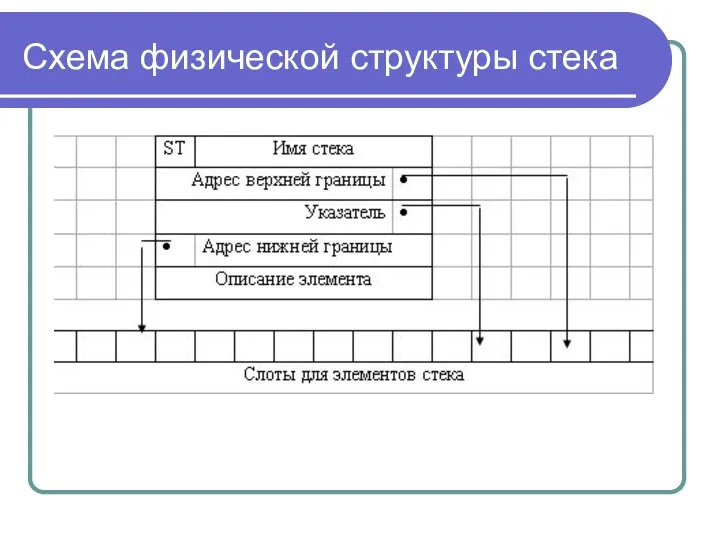
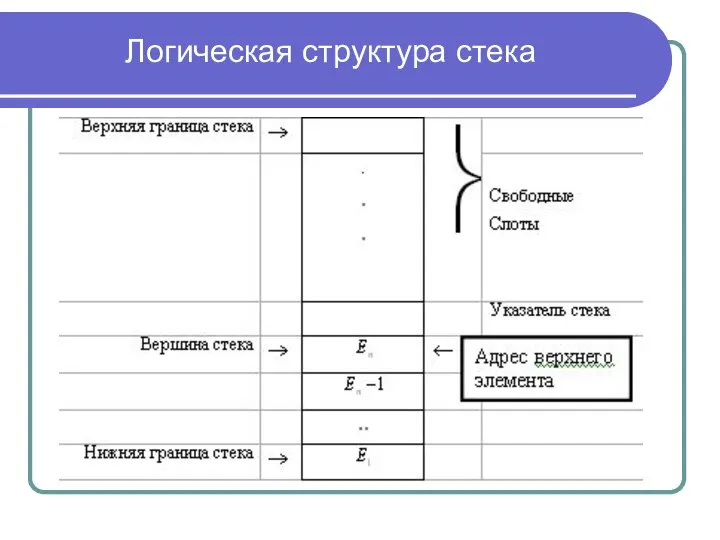
Стек (список LIFO — Last In First Out)
Слайд 23Схема физической структуры стека
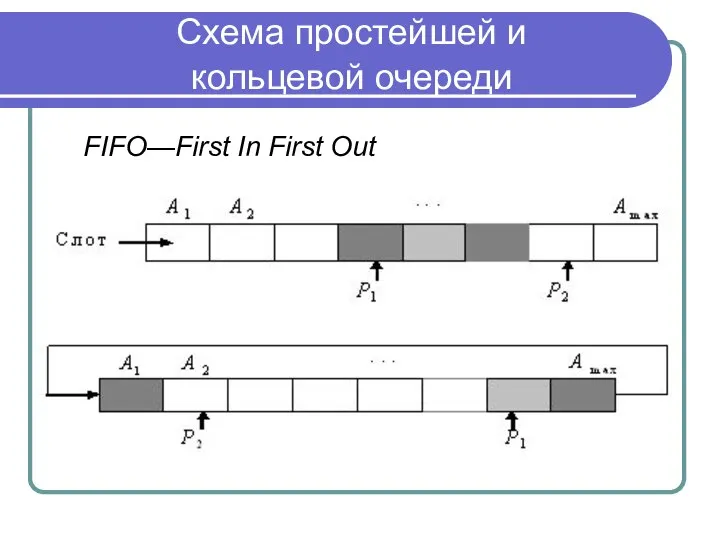
Слайд 24Схема простейшей и
кольцевой очереди
FIFO—First In First Out





















 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Элементы математического анализа
Элементы математического анализа Презентация на тему Логарифмическая функция, ее свойства и график
Презентация на тему Логарифмическая функция, ее свойства и график  Решение задач на многогранники, цилиндр, конус, шар
Решение задач на многогранники, цилиндр, конус, шар Перестановка слагаемых
Перестановка слагаемых Решение задач
Решение задач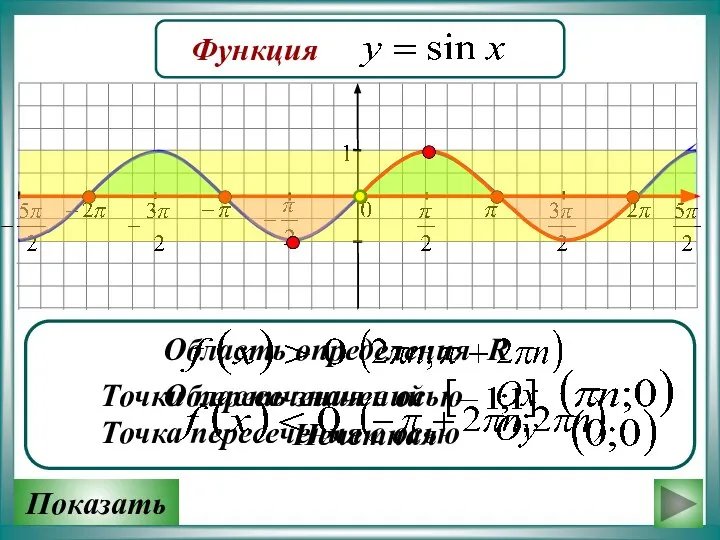 График функции y = sin x
График функции y = sin x Арксинус, арккосинус, арктангенс, арккотангенс
Арксинус, арккосинус, арктангенс, арккотангенс Элементы комбинаторики. Перестановки
Элементы комбинаторики. Перестановки Аналитические функции
Аналитические функции Уравнение касательной к графику функции
Уравнение касательной к графику функции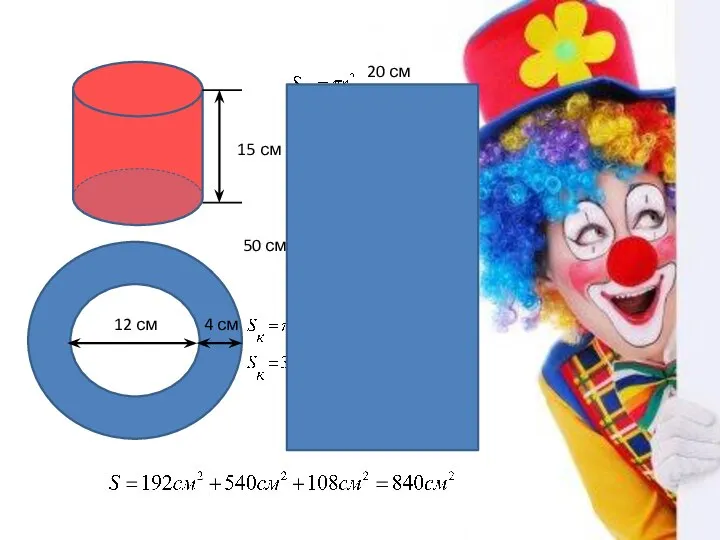 Площадь поверхности цилиндра
Площадь поверхности цилиндра Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Решение геометрических задач повышенного уровня сложности методом координат
Решение геометрических задач повышенного уровня сложности методом координат Теорема Пифагора
Теорема Пифагора Решение задач по теме Параллельные прямые
Решение задач по теме Параллельные прямые Основы анализа данных. Корреляционный анализ. (Лекция 5)
Основы анализа данных. Корреляционный анализ. (Лекция 5) Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла Игра-тренажер А знаете ли вы…. Математика 3 класс
Игра-тренажер А знаете ли вы…. Математика 3 класс Логика. Логические функции
Логика. Логические функции Умножение десятичных дробей
Умножение десятичных дробей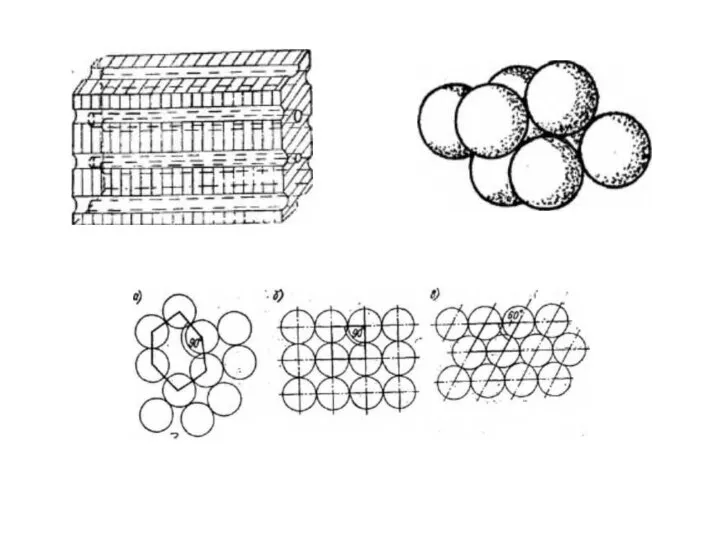 Кристаллическая решетка. Уравнения производной
Кристаллическая решетка. Уравнения производной Практические задачи
Практические задачи Системы линейных алгебраических уравнений. Лекция 3а
Системы линейных алгебраических уравнений. Лекция 3а Корни и степени чисел
Корни и степени чисел Площадь поверхности конуса
Площадь поверхности конуса Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Элементы теории множеств. Множества и основные операции над ними
Элементы теории множеств. Множества и основные операции над ними