Содержание
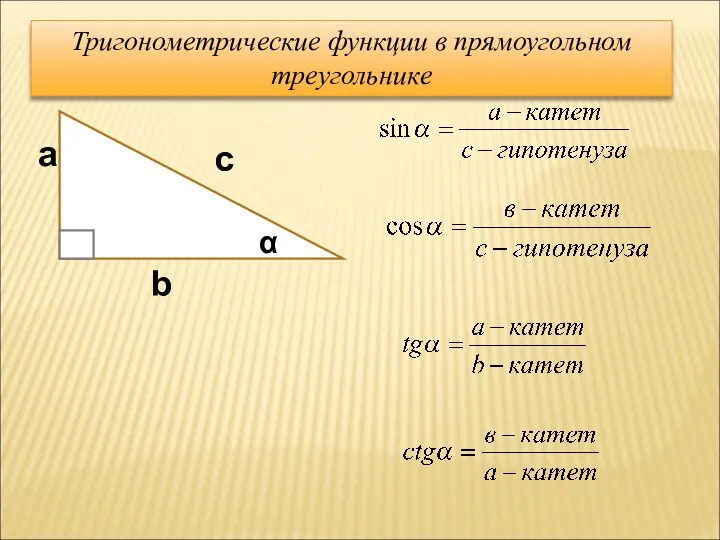
- 2. Тригонометрические функции в прямоугольном треугольнике α a b c
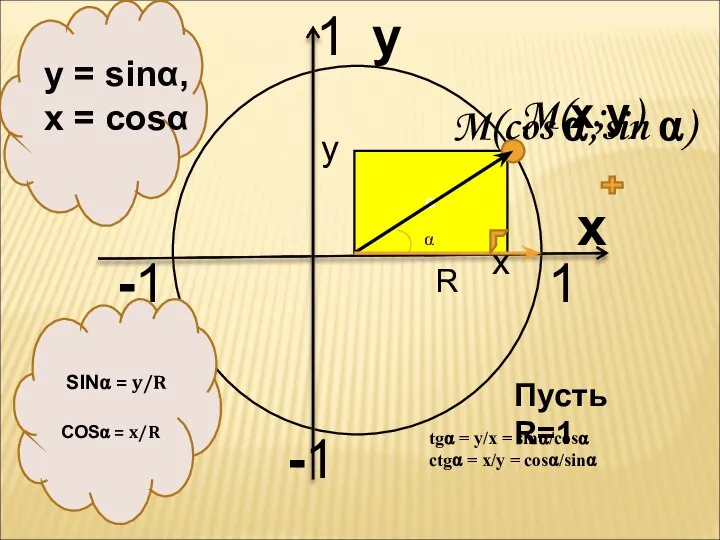
- 3. α M(х;у) y x x y 1 1 -1 -1 y = sinα, x = cosα
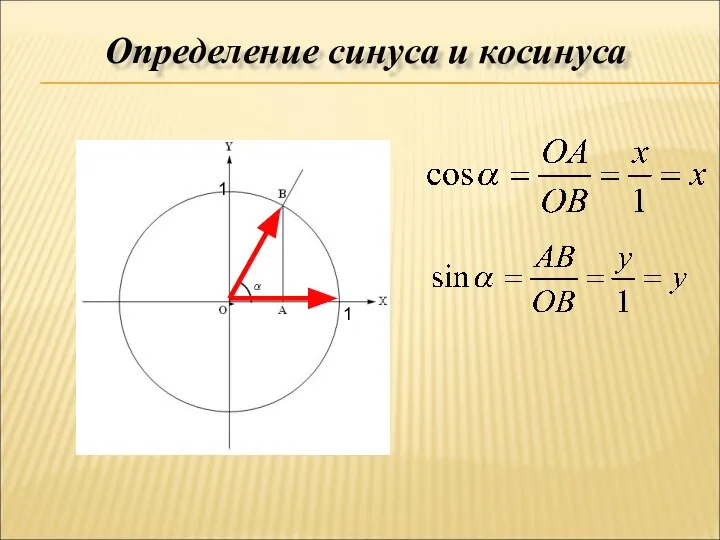
- 4. Определение синуса и косинуса 1 1
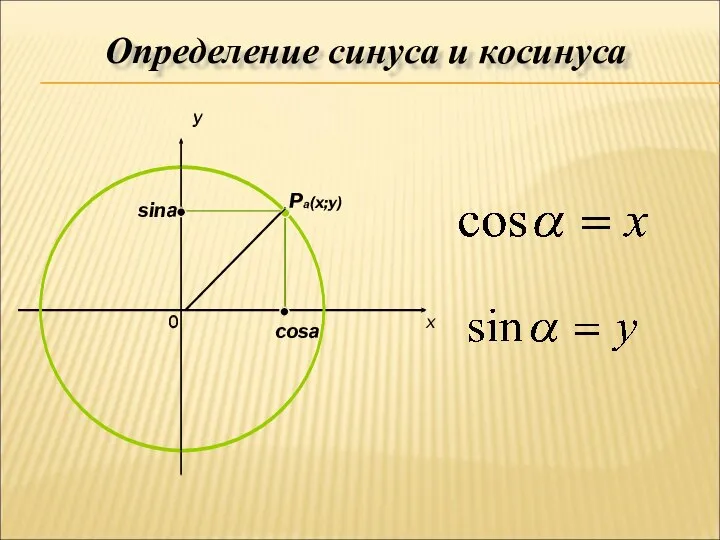
- 5. Определение синуса и косинуса
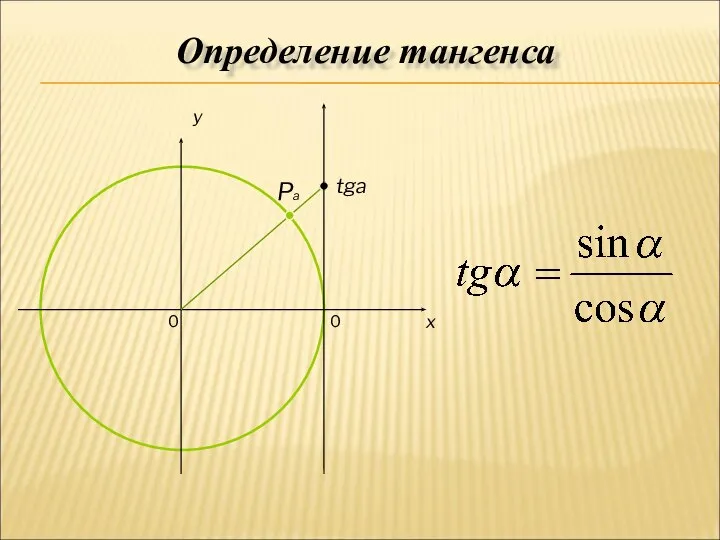
- 6. 0 x y tga Pa 0 Определение тангенса
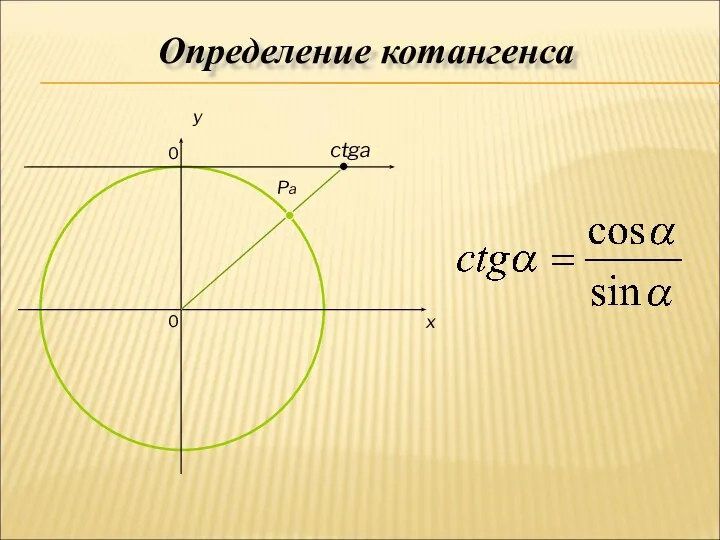
- 7. 0 x y ctga Pa 0 Определение котангенса
- 8. Основное тригонометрическое тождество 1
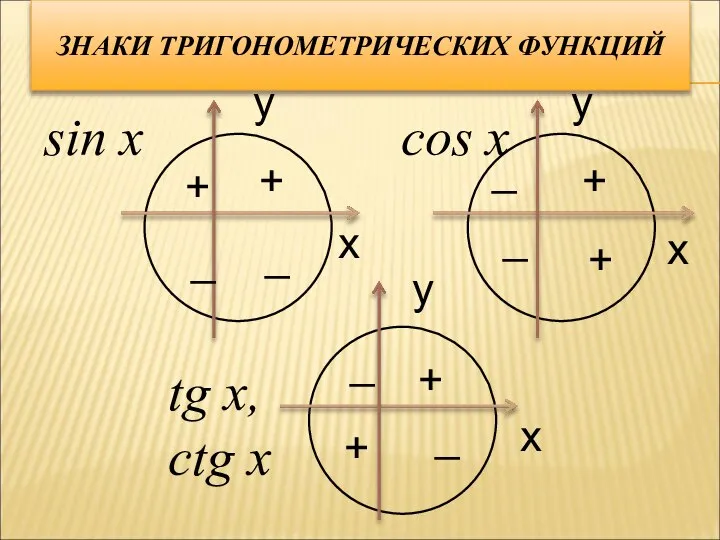
- 9. ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ sin x cos x tg x, ctg x x x x y y
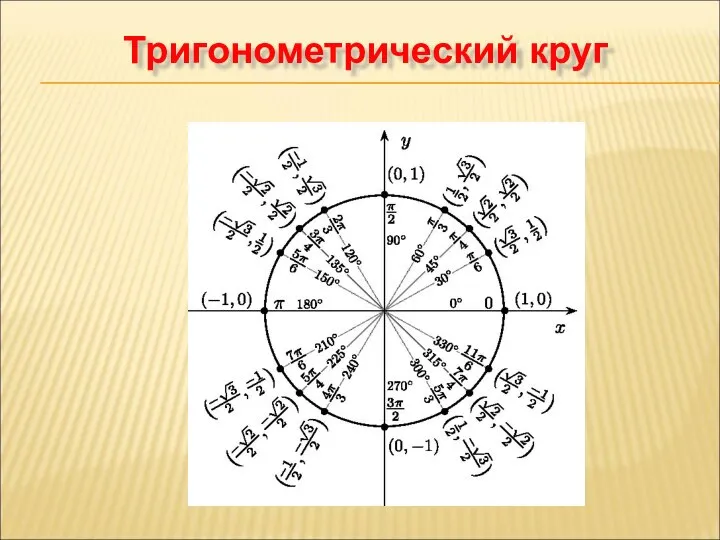
- 10. Тригонометрический круг
- 11. Задача Найти cos x, если sin x = - 15/17, π Решение: Sin 2 x +cos2
- 12. Решим вместе Знаки ответов зависят от четверти, в которой расположен аргумент х. В данном случае, четверть
- 13. ДОМАШНЕЕ ЗАДАНИЕ: На «3»: Сборник заданий для подготовки и проведения экзамена (СЭЗ). Варианты: 14,20,28,30,57,73,75,89 (во всех
- 15. Скачать презентацию




 Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Понятие цилиндра
Понятие цилиндра Решение логарифмических уравнений к занятию
Решение логарифмических уравнений к занятию Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла Основные формулы
Основные формулы Числовые промежутки
Числовые промежутки Оптические иллюзии
Оптические иллюзии Треугольник
Треугольник Умножение и деления дробей
Умножение и деления дробей Стереометрия. Школьный курс
Стереометрия. Школьный курс Разные задачи. Урок 140
Разные задачи. Урок 140 Теорема Пифагора. Урок геометрии в 8 классе
Теорема Пифагора. Урок геометрии в 8 классе Стереометрия. Аксиомы стереометрии. Часть 1
Стереометрия. Аксиомы стереометрии. Часть 1 Производная функции
Производная функции Прибавить и вычесть число 1
Прибавить и вычесть число 1 Векторы в пространстве. Понятие вектора
Векторы в пространстве. Понятие вектора Презентация на тему Кто хочет стать отличником
Презентация на тему Кто хочет стать отличником  УК Теория и примеры типовых задач. Проверка (испытание) гипотез
УК Теория и примеры типовых задач. Проверка (испытание) гипотез Умножение на три, треть числа Умножив три на единичку, Мы попадаем на страничку Из книги сказок для ребят Про ТРЕХ веселых порося
Умножение на три, треть числа Умножив три на единичку, Мы попадаем на страничку Из книги сказок для ребят Про ТРЕХ веселых порося Ряды динамики
Ряды динамики Модуль числа
Модуль числа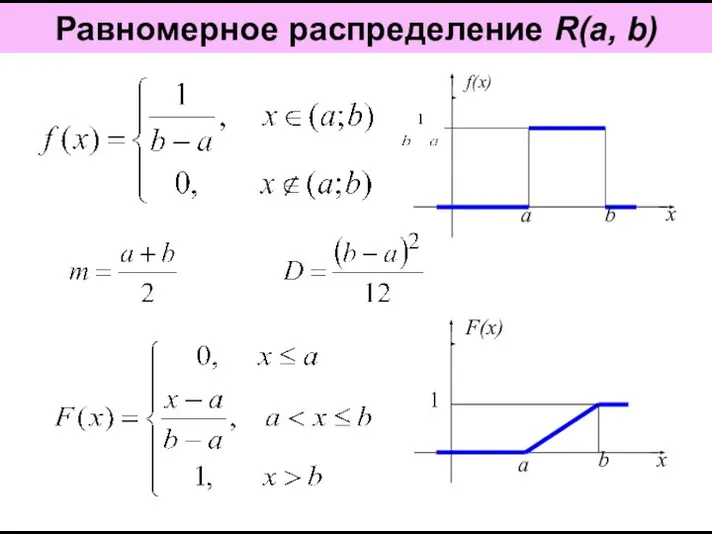 Равномерное распределение R(a, b)
Равномерное распределение R(a, b) Исследование функции с помощью производной
Исследование функции с помощью производной Математика в парикмахерском искусстве
Математика в парикмахерском искусстве Prezentatsia_Microsoft_PowerPoint(1)
Prezentatsia_Microsoft_PowerPoint(1) Страна геометрических фигур
Страна геометрических фигур Интерактивная дидактическая игра Сколько?
Интерактивная дидактическая игра Сколько? Решение задач
Решение задач