Содержание
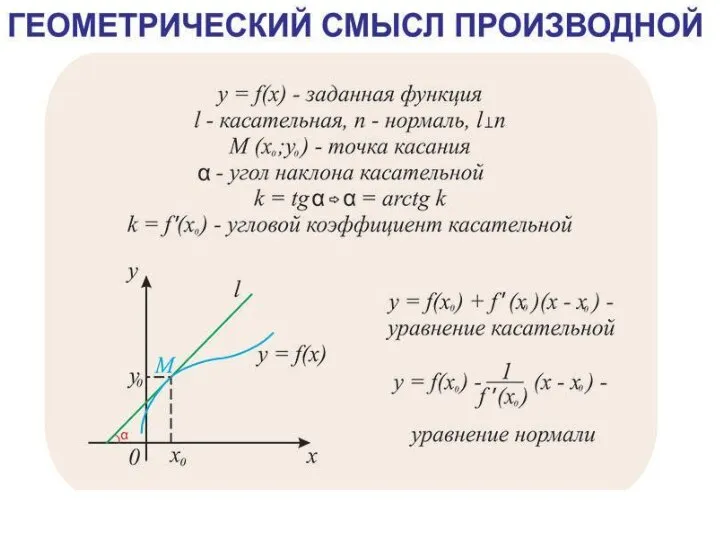
- 2. Геометрический смысл производной заключается в том, что её значение в рассматриваемой точке равняется угловому коэффициенту касательной,
- 4. Физический смысл производной заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью y =
- 7. №1. Составьте уравнение касательной и нормали к графику функции в точке с абсциссой х0=3.
- 8. №2. Материальная точка движется прямолинейно по закону x(t) = t2 − 13t + 23, где x
- 9. №3. Найдите производную указанного порядка
- 10. Задание 1. Вычислить производные первого и второго порядка для данных функций:
- 11. №4. Найдите ВСЕ отличные от нуля производные данной функции в указанной точке.
- 13. Скачать презентацию









 Презентация на тему Формулы сокращенного умножения (Сумма и разность кубов)
Презентация на тему Формулы сокращенного умножения (Сумма и разность кубов)  График линейной функции с модулем
График линейной функции с модулем Вероятность, статистика и функциональная грамотность в итоговой и промежуточной аттестации по математике
Вероятность, статистика и функциональная грамотность в итоговой и промежуточной аттестации по математике Простейшие задачи. Теоретический тест в координатах. 9 класс
Простейшие задачи. Теоретический тест в координатах. 9 класс Проецирование многогранных и кривых поверхностей
Проецирование многогранных и кривых поверхностей Корень п-ой степени
Корень п-ой степени Комбинаторика и азартные игры
Комбинаторика и азартные игры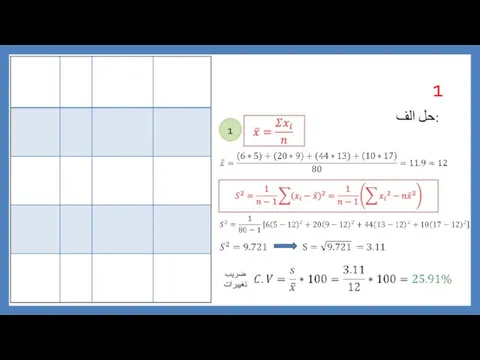 حل تمرین آمار
حل تمرین آمار Использование голосовых ассистентов на уроках математики в колледже
Использование голосовых ассистентов на уроках математики в колледже Ромб: признаки и свойства
Ромб: признаки и свойства Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Сравнение чисел. Геометрические величины. Геометрические фигуры
Сравнение чисел. Геометрические величины. Геометрические фигуры Приёмы умножения числа 2
Приёмы умножения числа 2 Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА
Презентация на тему РАЦИОНАЛЬНЫЕ ЧИСЛА  Презентация на тему Геометрические тела и окружающий мир
Презентация на тему Геометрические тела и окружающий мир  Интегрирование неотрицательніх измериміх функций
Интегрирование неотрицательніх измериміх функций Разбор Мат.Вертикали. 6 класс
Разбор Мат.Вертикали. 6 класс Метод рационализации в логарифмических неравенствах
Метод рационализации в логарифмических неравенствах user_file_54317c3324dbe (1)
user_file_54317c3324dbe (1) Понятие десятичной дроби. Разряды десятичных дробей
Понятие десятичной дроби. Разряды десятичных дробей Кроссворд Площади фигур
Кроссворд Площади фигур Тест. Свойство простейших фигур
Тест. Свойство простейших фигур Описанная окружность
Описанная окружность Презентация на тему Логарифмическая функция, ее свойства и график
Презентация на тему Логарифмическая функция, ее свойства и график  Старинные меры длины
Старинные меры длины Задача сетевого планирования с вложением средств
Задача сетевого планирования с вложением средств Обобщающий урок по теме Многогранники
Обобщающий урок по теме Многогранники Повторение пройденного (1 класс)
Повторение пройденного (1 класс)