Содержание
- 2. Метод возведения в степень Пример 1. Ответ: 2.
- 3. Пример 2. Ответ: 3.
- 4. Пример 3. . Проверка: х = - посторонний корень
- 5. Метод составления смешанной системы Ответ: 7. Решение уравнений вида
- 6. Ответ: 49. Метод введения новой переменной
- 8. Ответ: [5; 10]
- 9. Метод разложения подкоренного выражения на множители Ответ: 0,5.
- 10. Метод умножения на сопряженное выражение (1) Сложим данное уравнение с уравнением (1), получим: | : 2
- 11. Метод замены иррациональных уравнений системой рациональных уравнений a3 + 1 – 2a + a2 = 1
- 12. Использование монотонности Теорема. Если функция y = f(x) строго возрастает (убывает) на некотором промежутке I, то
- 13. Самостоятельная работа Задание: решите уравнение.
- 14. При решении уравнений вы можете воспользоваться подсказкой метода решения или, решив уравнение, проверить ответ
- 15. Пример 1.
- 16. Пример 2.
- 17. Пример 3.
- 18. Пример 4.
- 19. Пример 5.
- 20. Пример 6.
- 21. Пример 7.
- 22. Пример 8.
- 23. Пример 1. х Т.к. , то 2х = 4 х = 2 Показатели степени образуют бесконечную
- 24. Пример 2. Пусть y > 0. Получим уравнение Тогда у2 + 3у – 4 = 0
- 25. х = 4 Ответ: 4. Пример 3.
- 26. (1) | ∙ х=0 или Сложим данное уравнение с уравнением (1), получим Ответ: -3; 0; 3.
- 27. Пример 5. 1) 2) х – 3 = 27 х – 3 = -64 х =
- 28. Пример 6. 2х – 5 = у2 |y + 1| + |y + 3| = 14,
- 29. Пример 7. Пусть f(x) = Т.к. данная функция строго возрастает на D(f), то уравнение f(x) =
- 30. Метод возведения в степень . , то Проверка: х = - посторонний корень
- 31. х + 32 = 81 х = 49 Ответ: 49. Метод введения новой переменной
- 32. Метод составления смешанной системы Решение уравнений вида
- 33. Метод умножения на сопряженное выражение (1) 3х2 + 5х + 8 = 16 3х2 + 5х
- 34. Метод замены иррациональных уравнений системой рациональных уравнений a3 + 1 – 2a + a2 = 1
- 35. Использование монотонности Теорема. Если функция y = f(x) строго возрастает (убывает) на некотором промежутке I, то
- 36. Метод введения новой переменной. Пусть х = у2 + 1 |y – 2| + |y –
- 37. Ответ: [5; 10]
- 38. Метод разложения подкоренного выражения на множители Ответ: 0,5.
- 39. или х = 1 D Ответ: 1.
- 40. Проверка: х = Показатели степени образуют бесконечную убывающую геометрическую прогрессию, сумму которой можно найти по формуле
- 42. Скачать презентацию






![Ответ: [5; 10]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285641/slide-7.jpg)




























![Ответ: [5; 10]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285641/slide-36.jpg)



 Метод морфологического анализа
Метод морфологического анализа Worksheet 3 (reatke)
Worksheet 3 (reatke) Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике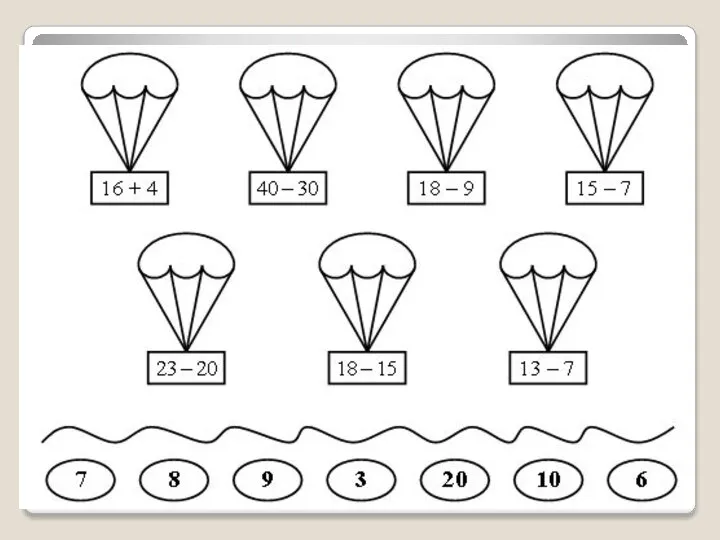 Задания Кириллу
Задания Кириллу Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений методом Гаусса Использование деревьев при решении алгоритмических задач
Использование деревьев при решении алгоритмических задач Признаки равенства треугольников. Равнобедренный треугольник
Признаки равенства треугольников. Равнобедренный треугольник Математические компоненты вычитания
Математические компоненты вычитания Таблицы и диаграммы
Таблицы и диаграммы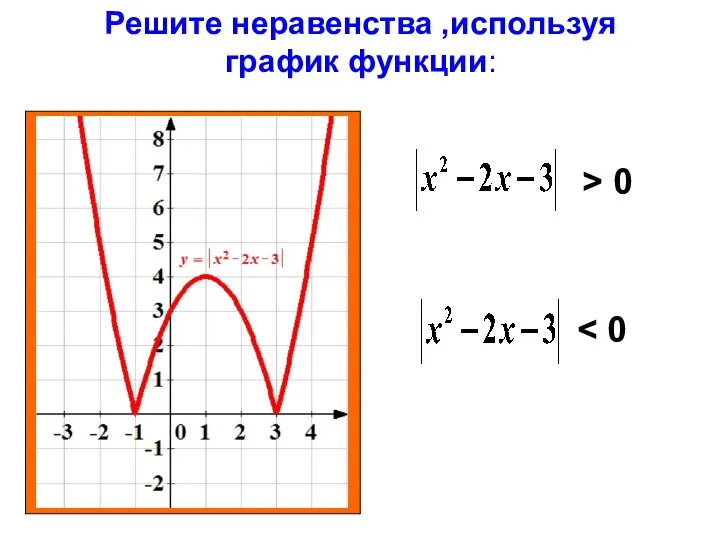 Решите неравенства ,используя график функции: x 2x 3 > 0
Решите неравенства ,используя график функции: x 2x 3 > 0 Призмы и антипризмы
Призмы и антипризмы Натуральные числа. Обобщающий урок
Натуральные числа. Обобщающий урок Квадратные уравнения
Квадратные уравнения Основные формулы
Основные формулы Дидактическая игра. Веселый ёжик
Дидактическая игра. Веселый ёжик Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Элементы аналитической геометрии на плоскости
Элементы аналитической геометрии на плоскости Формулы для нахождения площади треугольника
Формулы для нахождения площади треугольника VIII Международная олимпиада по математике для I курсов ССУЗ
VIII Международная олимпиада по математике для I курсов ССУЗ dispersionnyy-analiz(1)
dispersionnyy-analiz(1) Признаки равенства треугольников
Признаки равенства треугольников Признак существования определенного интеграла. Лекция №7
Признак существования определенного интеграла. Лекция №7 Решите уравнение (вариант 26 )
Решите уравнение (вариант 26 ) Вычитание натуральных чисел
Вычитание натуральных чисел Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Презентация на тему Магия Чисел
Презентация на тему Магия Чисел  Перетворення графіків функцій
Перетворення графіків функцій Повторение изученного материала, 1 класс
Повторение изученного материала, 1 класс