Тригонометрия. Измерение угловых величин

Тригонометрия - раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии.
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Измерение угловых величин
Угол - два различных луча с общим началом.
За измерение углов и дуг принимают угол в 1 градус (обозначают 10).
1/60 часть градуса называется минутой (обозначают 1’).
1/60 часть минуты называется секундой (обозначают 1‘’).

Измерение угловых величин
1 радиан - это еще одна единица измерения величины угла.
Угол в 1 радиан есть центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности.

Измерение угловых величин

Измерение угловых величин
Развернутый угол равен 180° или π радиан.
Используя соотношение 180° = π, можно угловую величину выражать как в радианах, так и в градусах.

Число π
Число π - математическая константа, выражающая отношение длины окружности к длине ее диаметра.
Число π имеет числовое значение, которое лежит в промежутке 3,1415926 < π < 3,1415927.
Таким образом угол

Определения тригонометрических функций:
Синус угла (sin α) - отношение противолежащего этому углу катета к гипотенузе.

Определения тригонометрических функций:
Косинус угла (cos α) - отношение прилежащего катета к гипотенузе.

Определения тригонометрических функций:
Тангенс угла (tg α) - отношение противолежащего катета к прилежащему.

Определения тригонометрических функций:
Котангенс угла (ctg α) - отношение прилежащего катета к противолежащему.

Важно помнить!
Область значений синуса и косинуса: от -1 до 1.
Иными словами синус и косинус принимают значения от -1 до 1.
Область значений тангенса и котангенса - вся числовая прямая, то есть эти функции могут принимать любые значения.

Единичная окружность
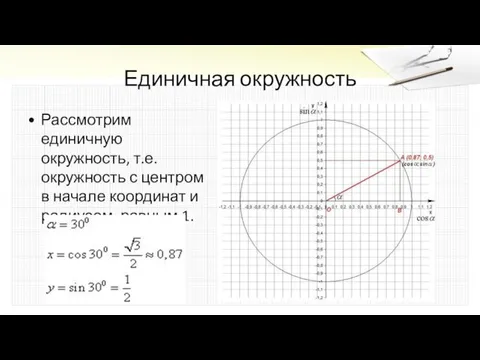
Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом, равным 1.

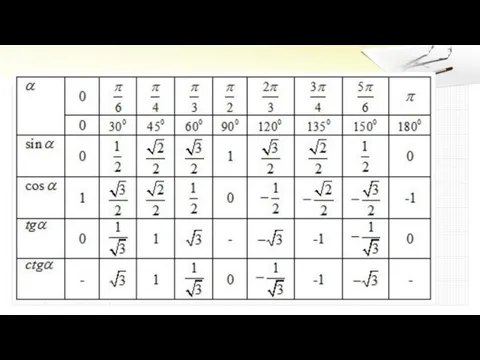
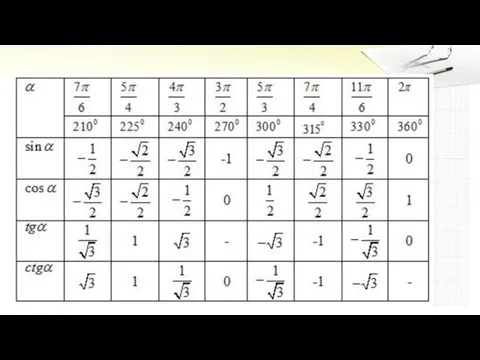
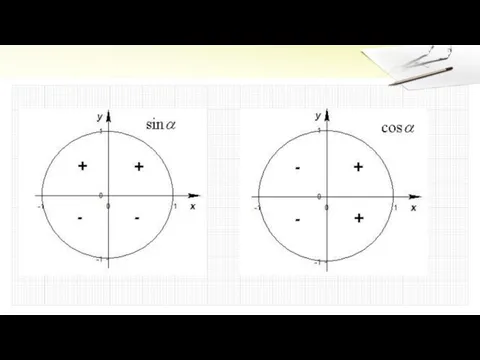
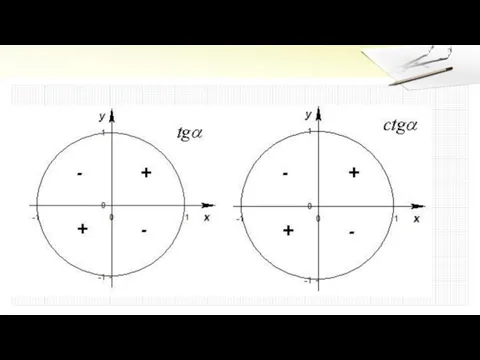
Тригонометрическую окружность разбивают на четверти.
В соответствующей четверти синус, косинус, тангенс, котангенс принимают положительное или отрицательное значения.