Слайд 2ТЕРМИНЫ
СИММЕТРИЯ — ЭТО СОРАЗМЕРНОСТЬ, ПРОПОРЦИОНАЛЬНОСТЬ ЧАСТЕЙ ЧЕГО-ЛИБО, РАСПОЛОЖЕННЫХ ПО ОБЕ СТОРОНЫ ОТ ЦЕНТРА.

ГОВОРЯ ПРОЩЕ, ЕСЛИ ОБЕ ЧАСТИ ОТ ЦЕНТРА ОДИНАКОВЫ, ТО ЭТО СИММЕТРИЯ.
ОСЬ СИММЕТРИИ ФИГУРЫ — ЭТО ПРЯМАЯ, КОТОРАЯ ДЕЛИТ ФИГУРУ НА ДВЕ СИММЕТРИЧНЫЕ ЧАСТИ. ЧТОБЫ НАГЛЯДНО ПОНЯТЬ, ЧТО ТАКОЕ ОСЬ СИММЕТРИИ, ВНИМАТЕЛЬНО РАССМОТРИТЕ РИСУНОК.
ЦЕНТР СИММЕТРИИ — ЭТО ТОЧКА, В КОТОРОЙ ПЕРЕСЕКАЮТСЯ ВСЕ ОСИ СИММЕТРИИ.
Слайд 5
РАЗБОР ЗАДАЧИ НА ЦЕНТРАЛЬНУЮ СИММЕТРИЮ
ДОКАЖИТЕ, ЧТО ПРИ ЦЕНТРАЛЬНОЙ СИММЕТРИИ ПЛОСКОСТЬ, ПРОХОДЯЩАЯ ЧЕРЕЗ

ЦЕНТР СИММЕТРИИ, ОТОБРАЖАЕТСЯ НА СЕБЯ.
Слайд 6РЕШЕНИЕ
О — ЦЕНТР СИММЕТРИИ, A— ДАННАЯ ПЛОСКОСТЬ, С-СЛУЧАЙНАЯ ТОЧКА НА ПЛОСКОСТИ.
ЕСЛИ

ТОЧКА О ∈ A, ТО ЛЮБАЯ ТОЧКА ПЛОСКОСТИ B ИМЕЕТ СИММЕТРИЧНУЮ ЕЙ ТОЧКУ ОТНОСИТЕЛЬНО O, ТОЖЕ ПРИНАДЛЕЖАЩУЮ ПЛОСКОСТИ A.
СЛЕДОВАТЕЛЬНО, ДЛЯ А ∈ A ЕЙ СИММЕТРИЧНАЯ ТОЧКА А1 ∈ A; ДЛЯ В ∈ A ТОЧКА B1∈ A; ДЛЯ С∈A ТОЧКА C1∈A.
ЧЕРЕЗ ТРИ ТОЧКИ А1, B1, С1 ПРИНАДЛЕЖАЩИЕ ПЛОСКОСТИ B, МОЖНО ПРОВЕСТИ ЕДИНСТВЕННУЮ ПЛОСКОСТЬ, СЛЕДОВАТЕЛЬНО, ОНА СОВПАДАЕТ С ПЛОСКОСТЬЮ A.





 Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм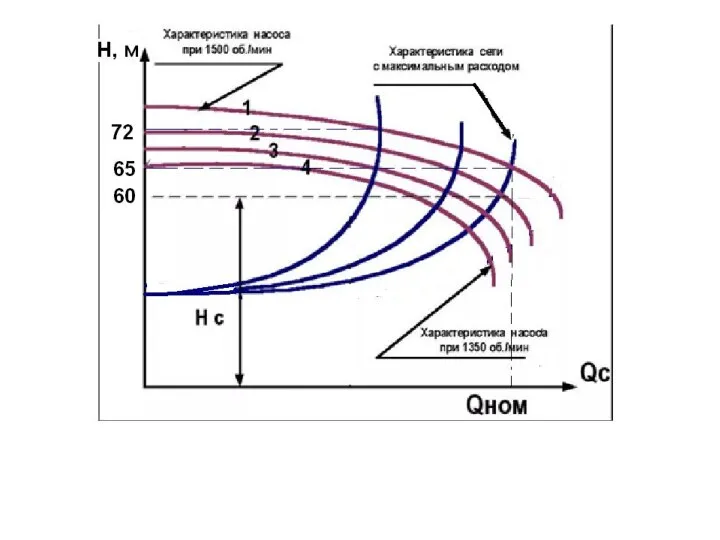 Модель частотно-регулируемого привода. (Тема 8)
Модель частотно-регулируемого привода. (Тема 8) Веселый счет. Викторина
Веселый счет. Викторина Производная сложной функции
Производная сложной функции Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые
Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые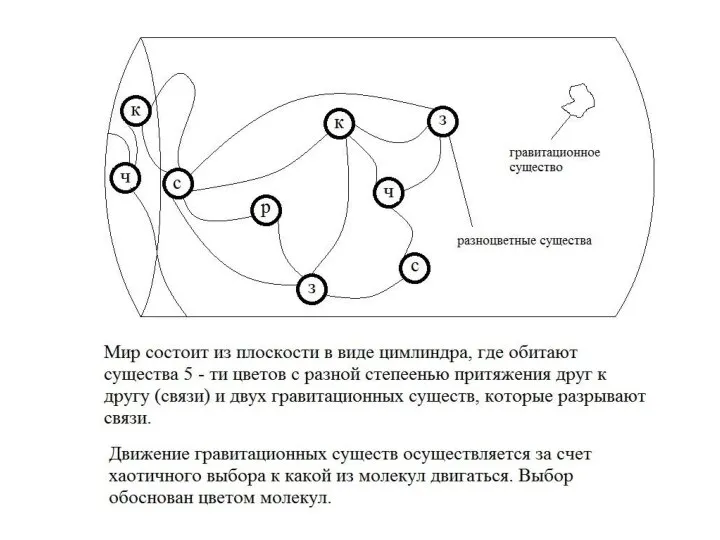 Мир в поверхности цилиндра
Мир в поверхности цилиндра Сложение чисел с разными знаками
Сложение чисел с разными знаками Многоугольники. Их формы
Многоугольники. Их формы Синус, косинус, тангенс и котангенс
Синус, косинус, тангенс и котангенс Развёртка куба
Развёртка куба Математика в танце
Математика в танце Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения Урок математики. 1 класс
Урок математики. 1 класс Ответы для самопроверки
Ответы для самопроверки Квадратный корень и его свойства
Квадратный корень и его свойства Математика в кинематографии
Математика в кинематографии Решение задач на готовых чертежах. Геометрия. 9 класс
Решение задач на готовых чертежах. Геометрия. 9 класс Презентация на тему Окружность и круг (5 класс)
Презентация на тему Окружность и круг (5 класс)  Работа над ошибками
Работа над ошибками Алгоритм вычисления площади с помощью палетки
Алгоритм вычисления площади с помощью палетки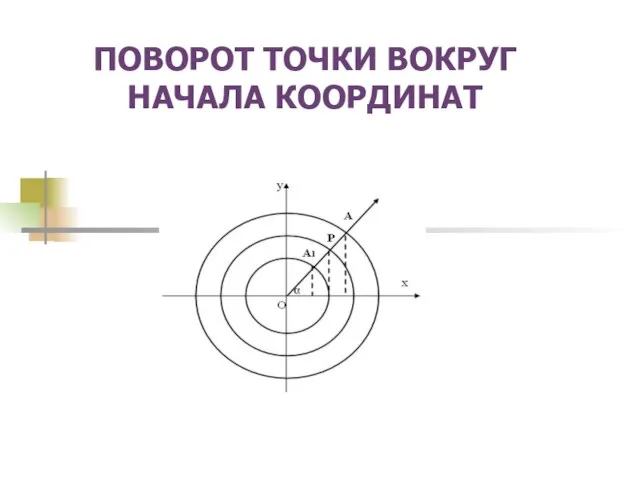 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Презентация на тему Параллелепипед (9 класс)
Презентация на тему Параллелепипед (9 класс)  Алгоритм фронта волны
Алгоритм фронта волны Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия
Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия