Содержание
- 2. Пусть математика сложна, Ее до края не познать, Откроет двери всем она, В них только надо
- 3. 1. Что такое треугольник? 2. Что такое прямоугольный треугольник? 3. Как называют стороны прямоугольного треугольника? -
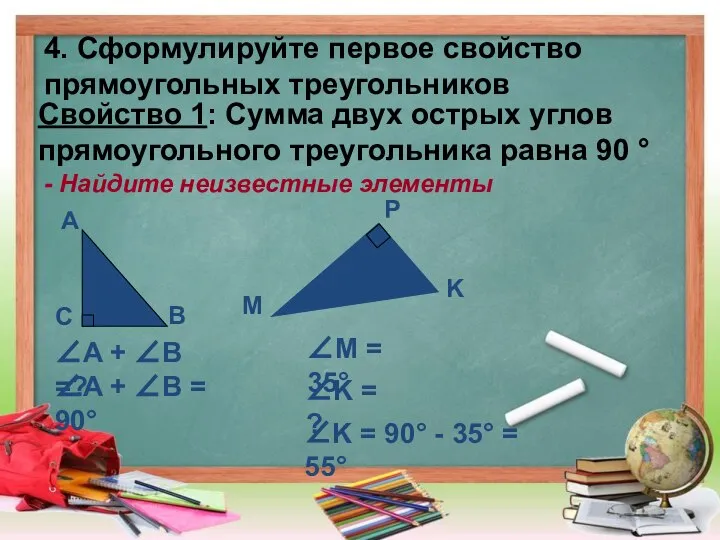
- 4. 4. Сформулируйте первое свойство прямоугольных треугольников Свойство 1: Сумма двух острых углов прямоугольного треугольника равна 90
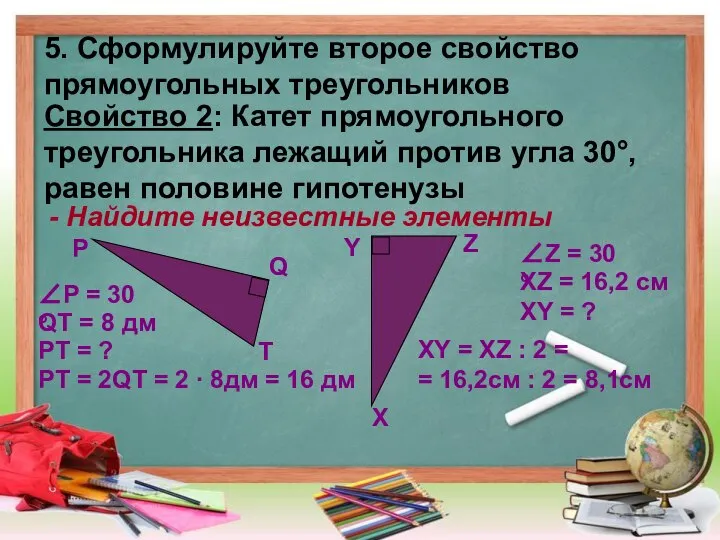
- 5. 5. Сформулируйте второе свойство прямоугольных треугольников Свойство 2: Катет прямоугольного треугольника лежащий против угла 30°, равен
- 6. 6. Сформулируйте третье свойство прямоугольных треугольников Свойство 3: Если катет прямоугольного треугольника равен половине гипотенузы, то
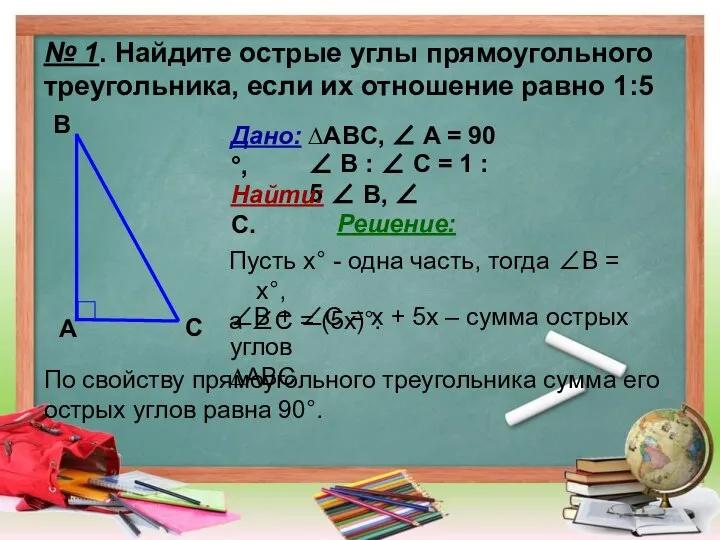
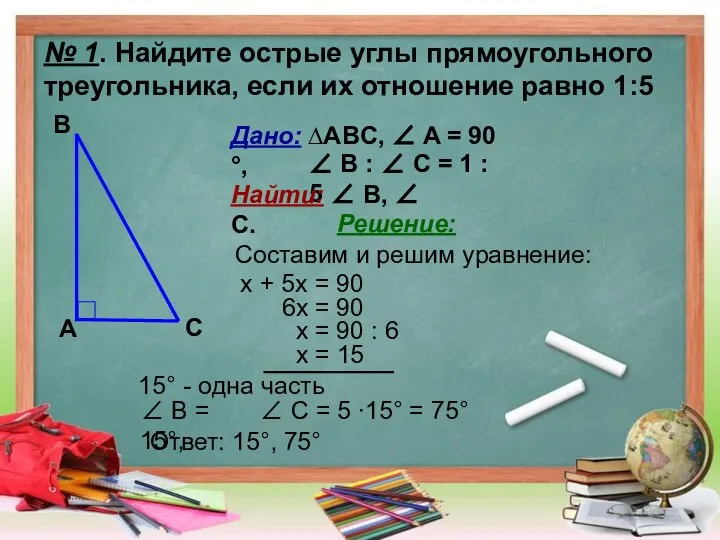
- 7. № 1. Найдите острые углы прямоугольного треугольника, если их отношение равно 1:5 А B C Дано:
- 8. № 1. Найдите острые углы прямоугольного треугольника, если их отношение равно 1:5 А B C Дано:
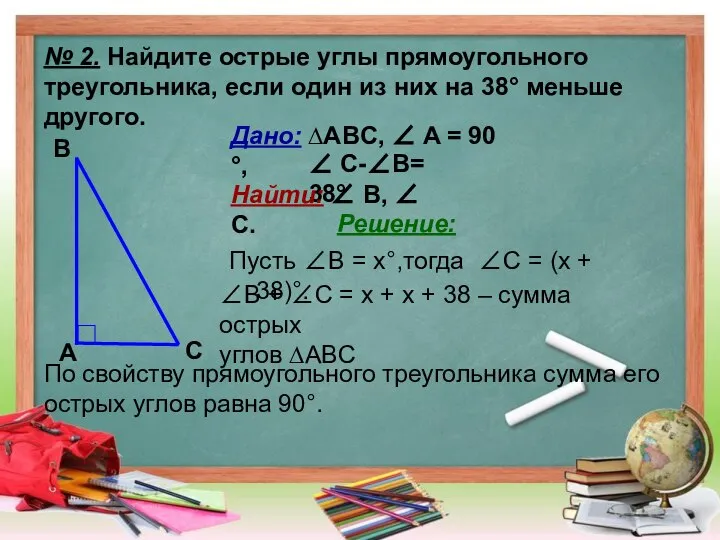
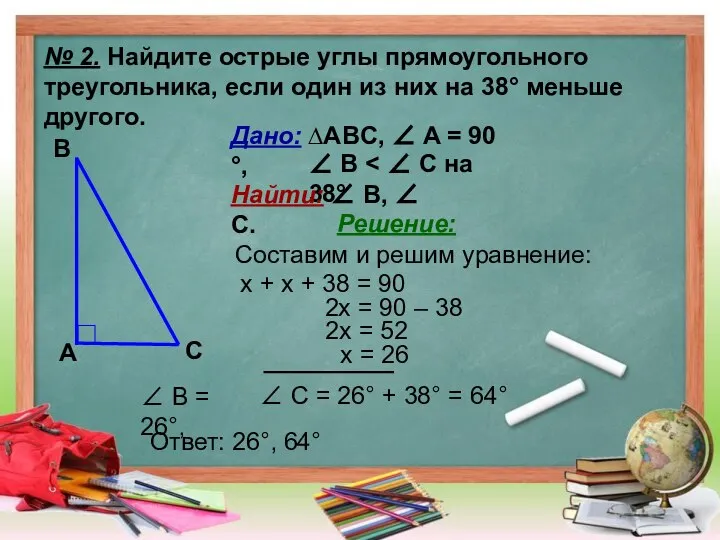
- 9. № 2. Найдите острые углы прямоугольного треугольника, если один из них на 38° меньше другого. А
- 10. № 2. Найдите острые углы прямоугольного треугольника, если один из них на 38° меньше другого. А
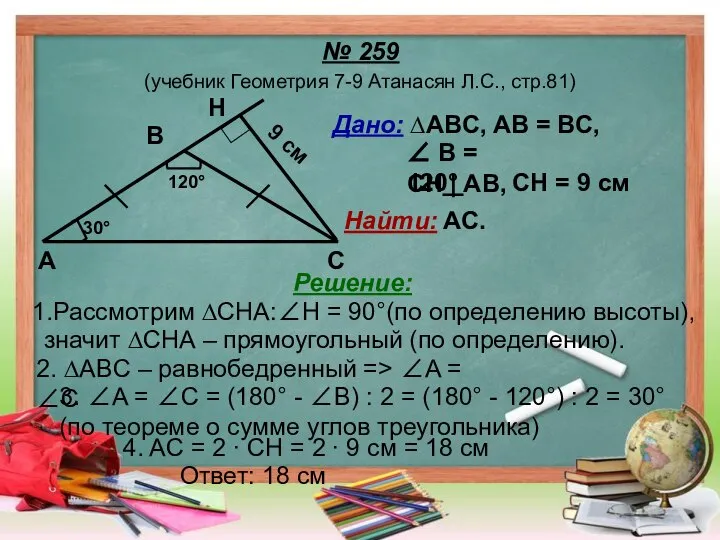
- 11. № 259 (учебник Геометрия 7-9 Атанасян Л.С., стр.81) Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота,
- 12. № 259 (учебник Геометрия 7-9 Атанасян Л.С., стр.81) Дано: ∆ABC, AB = BC, ∠ B =
- 13. Домашнее задание: Пункт 34 стр. 76-77 повторить, № 257,№260
- 15. Скачать презентацию





 Квадратный корень
Квадратный корень Планиметрия и стериометрия
Планиметрия и стериометрия Выражение длины вектора через его координаты
Выражение длины вектора через его координаты Различия между разными вариантами технологического процесса. Последовательный анализ
Различия между разными вариантами технологического процесса. Последовательный анализ Nepreryvnost_funktsii (1)
Nepreryvnost_funktsii (1) Уравнение и его корни
Уравнение и его корни Действия с алгебраическими дробями
Действия с алгебраическими дробями Метрология
Метрология Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена Алгоритм решения квадратного неравенства
Алгоритм решения квадратного неравенства Число 2. Цифра 2. Пара
Число 2. Цифра 2. Пара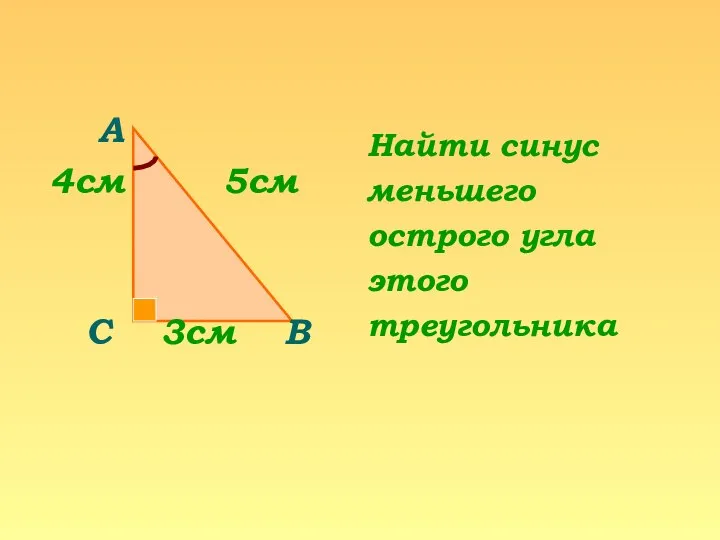 Устная работа на уроке геометрии
Устная работа на уроке геометрии Сечение тетраэдра
Сечение тетраэдра Поговорим о нуле
Поговорим о нуле Проценты
Проценты формулы нахождения периметра прямоугольника, периметра квадрата
формулы нахождения периметра прямоугольника, периметра квадрата Своя игра (4)
Своя игра (4) Определение понятия функция в толковых словарях
Определение понятия функция в толковых словарях Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Презентация на тему Прямая пропорциональность
Презентация на тему Прямая пропорциональность  20f
20f Презентация на тему Решение систем линейных уравнений 7 класс для учителя
Презентация на тему Решение систем линейных уравнений 7 класс для учителя  Квадратные уравнения
Квадратные уравнения Сумма n первых членов геометрической прогрессии
Сумма n первых членов геометрической прогрессии Метод наименьших квадратов
Метод наименьших квадратов Умножение натуральных чисел. Графический диктант. 5 класс
Умножение натуральных чисел. Графический диктант. 5 класс Симплекс-метод. Тема 4
Симплекс-метод. Тема 4 Разложение суммы тригонометрических функций в произведение и наоборот
Разложение суммы тригонометрических функций в произведение и наоборот