Слайд 2 В результате измерения физической величины мы получаем оценку этой величины - результат

измерений
При этом следует различать два понятия: истинные значения физических величин и их эмпирические проявления – действительные значения, которые являются результатами измерений и в конкретной измерительной задаче могут приниматься в качестве истинных значений
эмпирические - полученные опытным путём
Истинное значение Хи величины неизвестно и оно применяется только в теоретических исследованиях
Результаты измерений Хизм являются продуктами нашего познания и представляют собой приближённые оценки значений величин, полученных в процессе измерений
Слайд 3 Степень приближения полученных оценок к истинным значениям измеряемых величин зависит от многих

факторов: метода измерений, использованных средств измерений, от квалификации операторов, проводящих измерения, от условий, в которых проводятся измерения и т.д.
Поэтому между истинным значением физической величины и результатом измерений всегда имеется различие, которое выражается погрешностью измерений
Слайд 4 Погрешность результата измерения — отклонение результата измерения от истинного значения измеряемой величины:
∆X

= Xизм - Xи
Так как истинное значение величины всегда неизвестно, а на практике мы имеем дело с измеренными значениями величин, то формула измерения приобретает смысл только в том случае, когда известна погрешность измерения. А носителем известной погрешности является измерительный инструмент
С учётом этого формула измерения приобретает вид
Xизм = Xи ± ∆X
Погрешность измерительного инструмента определяют в процессе разработки измерительного инструмента
Слайд 5Источники погрешности измерений
Погрешность результата измерения, так же как и результат измерения, является

случайной величиной и имеет много составляющих, каждая из которых обусловлена различными факторами и источниками
источники появления погрешностей измерений:
Неполное соответствие объекта измерений принятой его модели;
Неполное знание измеряемой величины;
Неполное знание влияния условий окружающей среды на измерение;
Несовершенное измерение параметров окружающей среды;
Конечная разрешающая способность прибора или порог его чувствительности;
Неточность передачи значения единицы величины от эталонов к рабочим средствам измерений;
Неточные знания констант и других параметров, используемых в алгоритме обработки результатов измерения;
Аппроксимации и предположения, реализуемые в методе измерений;
Субъективная погрешность оператора при проведении измерений;
Изменения в повторных наблюдениях измеряемой величины при очевидно одинаковых условиях
и другие.
Слайд 6 Причины появления погрешностей измерений можно разделить на погрешности метода измерений, средств измерений

(инструмента) и оператора, проводящего измерения
В общем виде погрешность можно выразить следующей формулой:
∆X = ∆м + ∆и + ∆л
где ∆м – методическая погрешность (погрешность метода);
∆и - инструментальная погрешность (погрешность средств измерений);
∆л - личная (субъективная) погрешность
Слайд 7Методическая погрешность возникает из-за недостатков используемого метода измерений.
Чаще всего это является следствием

различных допущений при использовании эмпирических зависимостей между измеряемыми величинами или конструктивных упрощений в приборах, используемых в данном методе измерений.
Инструментальная погрешность - основные причины возникновения приведены в разделе о средствах измерений.
Субъективная погрешность связана с индивидуальными особенностями операторов - внимательность, сосредоточенность, быстрота реакции, степень профессиональной подготовленности.
Такая погрешность чаще встречается при большой доле ручного труда при проведении измерений и почти отсутствуют при использовании автоматизированных средств измерений.
Слайд 8Классификация погрешностей измерений
По характеру проявления они разделяются на систематические и случайные
Систематическая погрешность

– составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессирующие, периодические, изменяющиеся по сложному закону. Близость к нулю систематической погрешности отражает правильность измерений
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью








 Неравенство треугольника
Неравенство треугольника Дифференциальные уравнения в частных производных. Лекция1
Дифференциальные уравнения в частных производных. Лекция1 Изучение таблицы деления
Изучение таблицы деления Сложение вида +2, +3
Сложение вида +2, +3 Признаки равенства прямоугольных теугольников
Признаки равенства прямоугольных теугольников Фрактальное изображение
Фрактальное изображение Куб. Формулы для куба
Куб. Формулы для куба Десятичная запись дробных чисел
Десятичная запись дробных чисел Простейшие задачи в координатах
Простейшие задачи в координатах Теория вероятностей и математическая статистика. Лекция 6 ТВ
Теория вероятностей и математическая статистика. Лекция 6 ТВ Производная функции. Обобщающий урок
Производная функции. Обобщающий урок Решение систем линейных уравнений при помощи компьютерных технологий
Решение систем линейных уравнений при помощи компьютерных технологий Зависимость в математике
Зависимость в математике Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток
Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток Производные и дифференциалы
Производные и дифференциалы Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Презентация на тему ТРАПЕЦИЯ. ПЛОЩАДЬ ТРАПЕЦИИ
Презентация на тему ТРАПЕЦИЯ. ПЛОЩАДЬ ТРАПЕЦИИ  Решение задач
Решение задач Справочник по геометрии
Справочник по геометрии Средняя линия треугольника
Средняя линия треугольника ЕГЭ. Экономические задачи VI
ЕГЭ. Экономические задачи VI Математика с котом Леопольдом
Математика с котом Леопольдом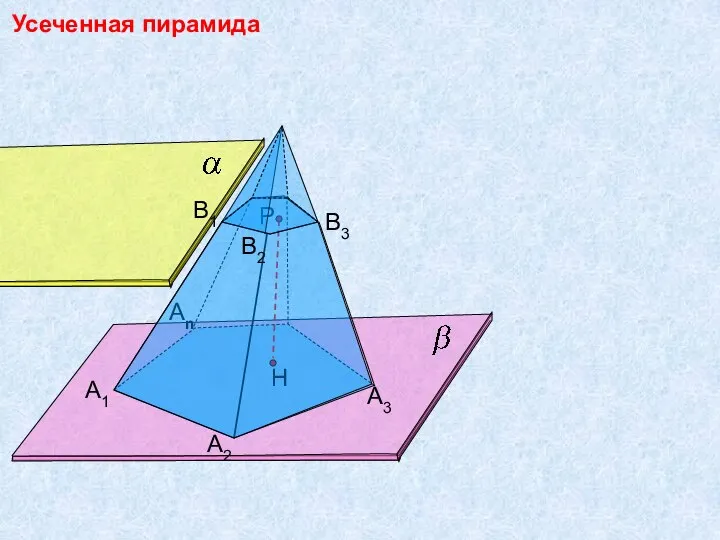 Усеченная пирамида
Усеченная пирамида П 3
П 3 Статистическая теория радиотехнических систем. Корреляционный анализ детерминированных процессов. (Лекция 4)
Статистическая теория радиотехнических систем. Корреляционный анализ детерминированных процессов. (Лекция 4) Примеры расчета матриц
Примеры расчета матриц Понятие матрица
Понятие матрица Окружность. Комбинации с окружностью. ЕГЭ
Окружность. Комбинации с окружностью. ЕГЭ