- Главная
- Математика
- Умножение матрицы на число

Содержание
- 2. Что такое матрица? Это математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например,
- 3. История Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было
- 4. Умножение матрицы A на число λϵK заключается в построении матрицы λA(λaij).
- 5. Свойства умножения матрицы на число 1. 1*A = A; Ө*A= Ө, где Ө-нулевая матрица 2. (λβ)*A
- 6. Примеры
- 7. Применение В физике и других прикладных науках матрицы – являются средством записи данных и их преобразования.
- 8. Список литературы Беллман Р. Введение в теорию матриц. — М.: Мир, 1969. Ильин В. А., Позняк
- 10. Скачать презентацию
Слайд 2Что такое матрица?
Это математический объект, записываемый в виде прямоугольной таблицы элементов кольца
Что такое матрица?
Это математический объект, записываемый в виде прямоугольной таблицы элементов кольца

или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задает размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);
в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);
умножение матрицы на элемент основного кольца или поля (то есть скаляр).
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);
в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);
умножение матрицы на элемент основного кольца или поля (то есть скаляр).
Слайд 3История
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом».
Основным применением
История
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом».
Основным применением

матриц было решение линейных уравнений. Также волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц.
После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-м столетии и опубликовал «правило Крамера» в 1751 году.
Примерно в этом же промежутке времени появился «метод Гаусса».
Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-м столетии и опубликовал «правило Крамера» в 1751 году.
Примерно в этом же промежутке времени появился «метод Гаусса».
Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
Слайд 4Умножение матрицы A на число λϵK заключается в построении матрицы λA(λaij).
Умножение матрицы A на число λϵK заключается в построении матрицы λA(λaij).
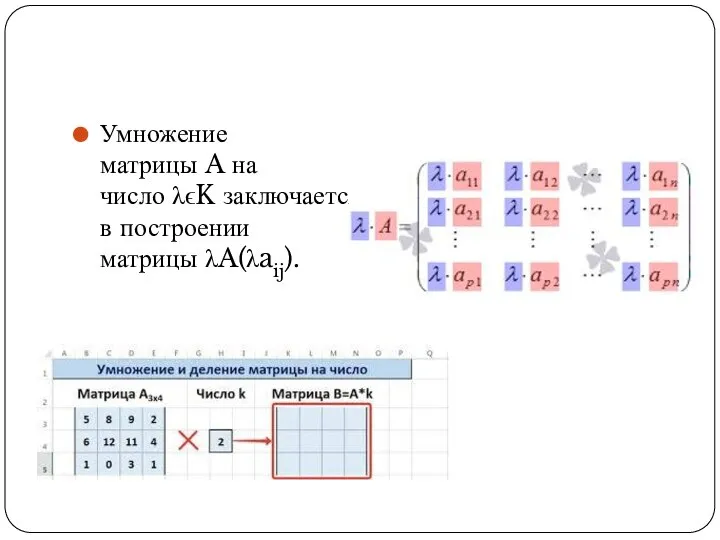
Слайд 5Свойства умножения матрицы на число
1. 1*A = A;
Ө*A= Ө, где Ө-нулевая матрица
2. (λβ)*A = λ*(βA)
3. (λ+β)*A
Свойства умножения матрицы на число
1. 1*A = A;
Ө*A= Ө, где Ө-нулевая матрица
2. (λβ)*A = λ*(βA)
3. (λ+β)*A
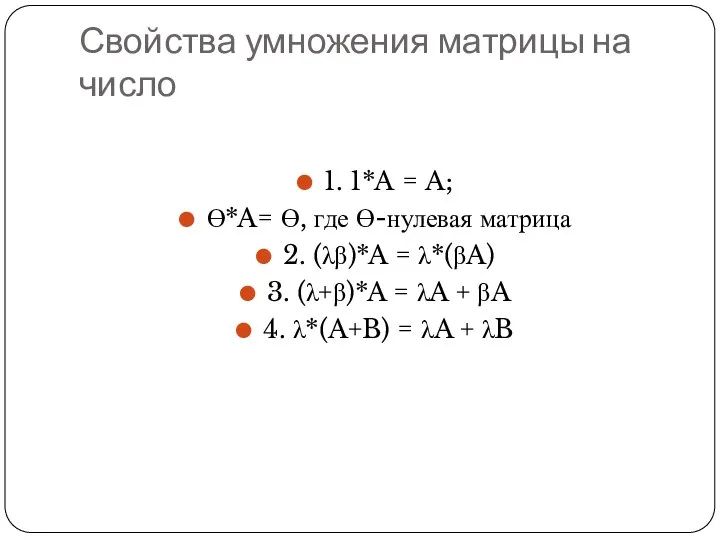
= λA + βA
4. λ*(A+B) = λA + λB
4. λ*(A+B) = λA + λB
Слайд 6Примеры
Примеры

Слайд 7Применение
В физике и других прикладных науках матрицы – являются средством записи данных
Применение
В физике и других прикладных науках матрицы – являются средством записи данных

и их преобразования. В программировании – в написании программ. Они еще называются массивами. Широко применение и в технике. Например, любая картинка на экране – это двумерная матрица, элементами которой являются цвета точек.
В психологии понимание термина сходно с данным термином в математике, но взамен математических объектов подразумеваются некие "психологические объекты" – например, тесты.
Кроме того, матрицы имеет широкое применение в экономике, биологии, химии и даже в маркетинге.
В психологии понимание термина сходно с данным термином в математике, но взамен математических объектов подразумеваются некие "психологические объекты" – например, тесты.
Кроме того, матрицы имеет широкое применение в экономике, биологии, химии и даже в маркетинге.
Слайд 8Список литературы
Беллман Р. Введение в теорию матриц. — М.: Мир, 1969.
Ильин В. А., Позняк Э.
Список литературы
Беллман Р. Введение в теорию матриц. — М.: Мир, 1969.
Ильин В. А., Позняк Э.

Г. Основы математического анализа (в двух частях). — М.: Физматлит, 2005.
Кричевец А.Н., Шикин Е.В., Дьячков А.Г. Математика для психологов. – М.: ФЛИНТА, 2013
Курош А. Г. Курс высшей алгебры. (9-е изд.) — М.: Наука, 1968
Светлаков А.Н. – видеолекции с сайта http://mathdialogue.livejournal.com/
Кричевец А.Н., Шикин Е.В., Дьячков А.Г. Математика для психологов. – М.: ФЛИНТА, 2013
Курош А. Г. Курс высшей алгебры. (9-е изд.) — М.: Наука, 1968
Светлаков А.Н. – видеолекции с сайта http://mathdialogue.livejournal.com/
Следующая -
Арены. Бензол Промежуточная аттестация по геометрии
Промежуточная аттестация по геометрии Математический дизайн
Математический дизайн Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика
Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Основные понятия комбинаторики. Факториал. Вычисление факториала
Основные понятия комбинаторики. Факториал. Вычисление факториала Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений Образец решения уравнения х2=а
Образец решения уравнения х2=а Табличный метод решения задач ЕГЭ по теории вероятностей
Табличный метод решения задач ЕГЭ по теории вероятностей Практикум. Демографические задачи
Практикум. Демографические задачи Приёмы умножения числа 2
Приёмы умножения числа 2 Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные
Преобразование обыкновенных дробей в десятичные и десятичных в обыкновенные Случайные события
Случайные события Тела вращения
Тела вращения Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Основы матричной алгебры
Основы матричной алгебры элементы теории множеств
элементы теории множеств Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости Презентация на тему Построение треугольника по трем элементам
Презентация на тему Построение треугольника по трем элементам  Производная сложной функции
Производная сложной функции Предмет вычислительной математики. Численные методы
Предмет вычислительной математики. Численные методы Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Треугольник
Треугольник Показательная функция
Показательная функция praktika_3
praktika_3 Задания с фигурами
Задания с фигурами Математика. Проверочная работа
Математика. Проверочная работа Переменные величины и их свойства
Переменные величины и их свойства Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"