Слайд 2Понятия логической формулы и ее ранга
Опр. Высказывание с заданным значением истинности называется

ло-гической постоянной (F и Т), а высказывание, значение истинности которого не задано, называется логической переменной.
Опр. Всякое простое высказывание (логическая переменная или логи-ческая постоянная), а также всякое сложное высказывание, образованное из простых с помощью логических операций, называется логической формулой.
Слайд 3Обозначение: Ф, Ф1, Ф2, … Если в формулу Ф входят высказывания Х1,

Х2,…, Хп, то в общем виде формулу обозначают Ф(X1, Х2,…, Xn).
Например:
1) Ф1 = А ˅ ¬В ˄ (С → А)
2) Ф2 = ((А → У) ˄ В) ↔ (¬Х ˅ У)
Слайд 4Ранг формулы
Опр. Рангом формулы A называется число всех логических операций, с помощью

которых эта формула образована.
Обозначение: r (Ф)
Так, r (Ф1) = 4, r (Ф2) = 5
(!!) Очевидно, что ранг простого высказывания равен нулю.
Слайд 5Правила чтения формул
1. Если скобки отсутствуют, то логические операции выполняются в следующей

очередности: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
2. Если без скобок записаны друг за другом несколько одинаковых операций, то они выполняются последовательно слева направо.
3. Операция отрицания записывается без скобок и применяется ко всей формуле, записанной под символом отрицания.
4. При необходимости изменить естественный порядок действий часть формулы заключается в скобки.
Слайд 6Классификация формул. Понятие о их равносильности
Опр. Формула Ф(X1,…, Xn) называется выполнимой, если

она прини-мает значение 1 хотя бы при одном наборе значений Х1,…, Хп.
Опр. Формула Ф(X1,…, Xn) называется тождественно истинной (за-коном логики), если она принимает значение 1 при любом наборе значений Х1,…, Хп.
Напр.: Х ˅ Х
Опр. Формула Ф(X1,…, Xn) называется тождественно ложной (про-тиворечием), если она принимает значение 0 при любом наборе значений Х1, …, Хп.
Напр.: Х ˄ Х
Слайд 7Опр. Две формулы Ф1 и Ф2 называется равносильными, если они при-нимают одинаковые

значения при каждом наборе значений Х1, Х2, …, Хп.
Обозначение: Ф1 ≡ Ф2
Решить вопрос о равносильности формул можно с помощью их истин-ностных таблиц.
ПР. Докажем две равносильности, которые следует помнить.
Слайд 9Основные равносильности алгебры высказываний
1. Операции конъюнкция и дизъюнкция коммутативны:
А ˄ В ≡

В ˄ А
А ˅ В ≡ В ˅ А
2. Операции конъюнкция и дизъюнкция ассоциативны:
(А ˄ В) ˄ С ≡ А ˄ (В ˄ С)
(А ˅ В) ˅ С ≡ А ˅ (В ˅ С)
Слайд 103. Операции конъюнкция и дизъюнкция связаны между собой свойством дистрибутивности:
А ˄ (В

˅ С) ≡ А ˄ В ˅ А ˄ С
А ˅ (В ˄ С) ≡ (А ˅ В) ˄ (А ˅ С)
4. Свойства логических констант:
А ˄ Т ≡ А
А ˄ F ≡ F
А ˅ Т ≡ T
А ˅ F ≡ A
Слайд 13Три основные формы мышления.
Понятие – это форма мышления, в которой отражаются существенные

признаки объектов, относящихся к данному понятию. Например, «Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны» (определение понятия «медиана треугольника»).
Суждение – это форма мышления, в которой что-либо утверждается или отрицается о существовании предметов, о связи между ними и их свойствами или отношениях между ними. Например, «В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой» (теорема).
Умозаключение – это форма мышления, посредством которой из одного или нескольких суждений получается новое суждение. Например, доказательство любой теоремы, например теоремы о медиане равнобедренного треугольника, представляет собой цепочку умозаключений.
Слайд 14Умозаключение как форма мышления
Суждения образуются в мышлении двумя основными способами:
1. Непосредственно (с

помощью суждения выражается результат восприятия). Например, суждение «эта фигура – окружность».
2. Опосредованно (суждение возникает в результате особой мыслительной деятельности, называемой умозаключением). Например, «множество данных точек плоскости таково, что их расстояние от одной точки одинаково; значит, эта фигура – окружность».
Слайд 15Законы логики, используемые в умозаключениях

Слайд 18Понятие о теоремах. Прямая, обратная и противоположная
теоремы. Необходимые и достаточные условия
Теорема –

это некоторая импликация высказываний, т.е. Т ≡А →В
При этом высказывание А называется условием теоремы, а В – ее заключением.
Если в теореме А и В простые высказывания, то теорема называется простой, в противном случае - сложной.
Слайд 21Методы доказательств теорем
I. Схемы прямого доказательства

Слайд 24Доказательство теорем методом от противного

Слайд 25Упростите формулу с помощью равносильных преобразований:

Слайд 27Домашнее задание
Упростите формулу с помощью равносильных преобразований:

























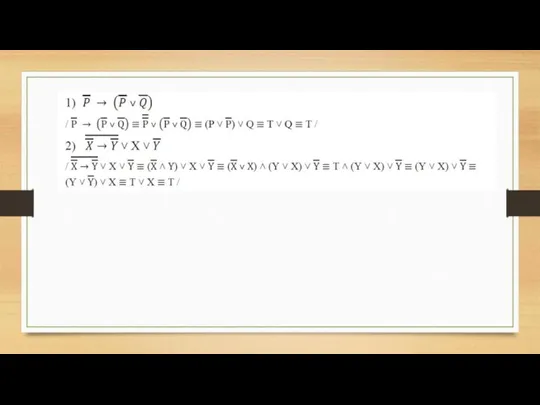

 Упрощение логических операций
Упрощение логических операций Теорема Пифагора
Теорема Пифагора История системы мер длины (часть 2)
История системы мер длины (часть 2) Probability Distributions
Probability Distributions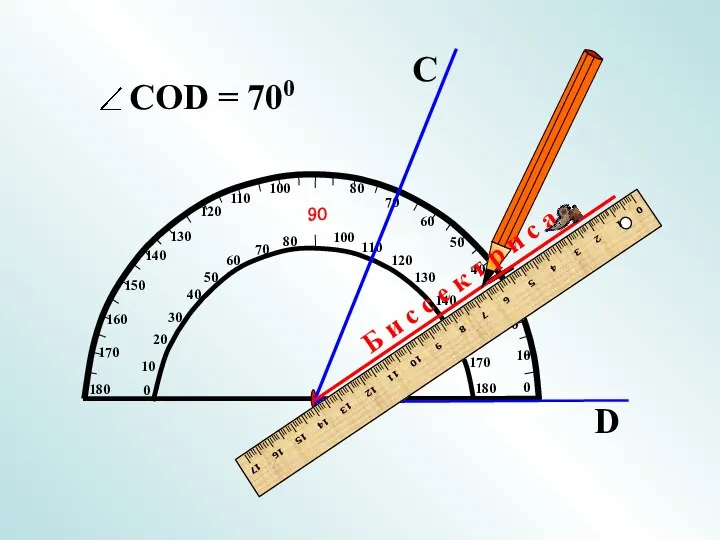 Биссектриса угла
Биссектриса угла Деление вида a:а, а:1
Деление вида a:а, а:1 Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов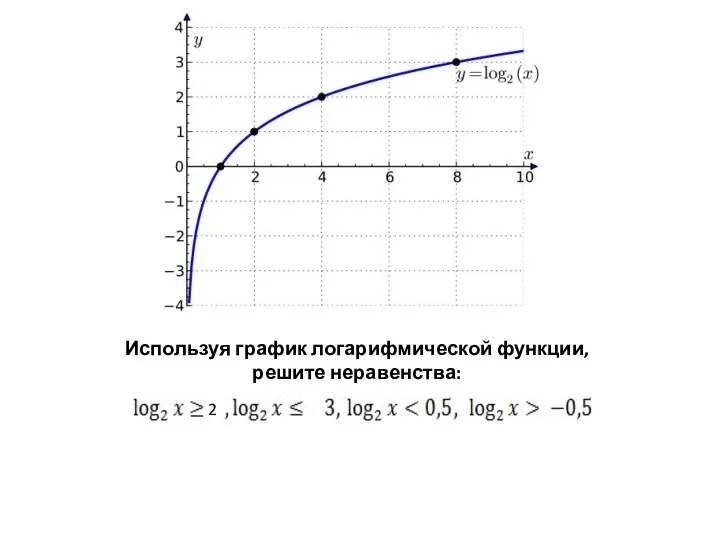 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Матрица размера m x n
Матрица размера m x n Тренажер Состав числа
Тренажер Состав числа Отношения и золотое сечение
Отношения и золотое сечение Параллелограмм и его свойства и признаки
Параллелограмм и его свойства и признаки Страна Математика
Страна Математика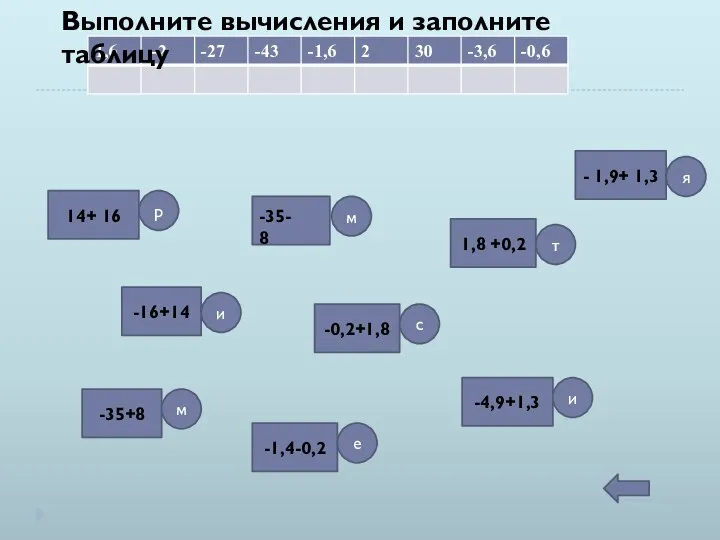 Выполните вычисления и заполните таблицу. 6 класс
Выполните вычисления и заполните таблицу. 6 класс Матрицы и определители
Матрицы и определители Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Веселое путешествие
Веселое путешествие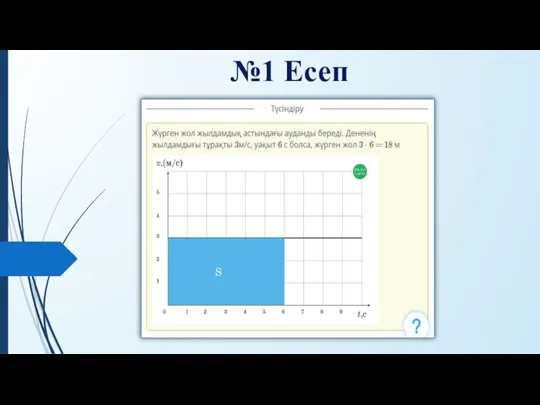 Есептер шығару
Есептер шығару Наши истинные учителя опыт и чувства. Из истории геометрии
Наши истинные учителя опыт и чувства. Из истории геометрии Параллельность прямых. Урок – практикум
Параллельность прямых. Урок – практикум Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Приближение вычисления
Приближение вычисления Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Смешаное число
Смешаное число Состав числа (домики)
Состав числа (домики) Сопоставление эмпирических и теоретических частот
Сопоставление эмпирических и теоретических частот