Содержание
- 2. Пересечение А ∩ В – это множество элементов, принадлежащих одновременно А и В. Пример: А \
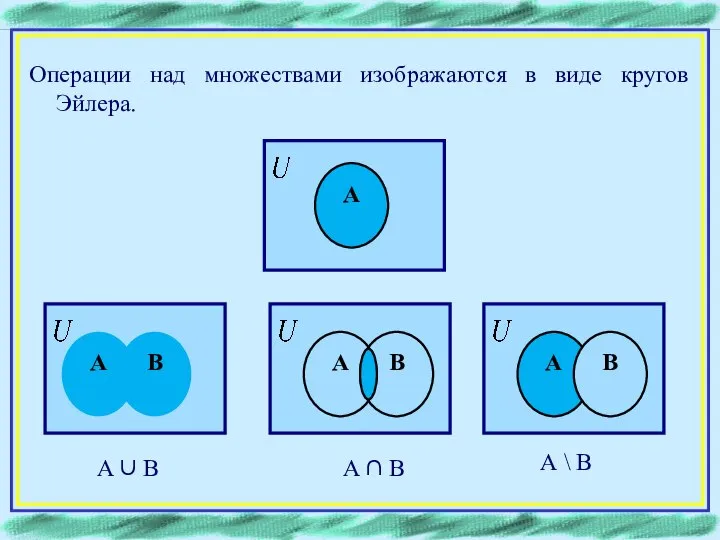
- 3. Операции над множествами изображаются в виде кругов Эйлера. А А В А ∪ В А В
- 4. А В В А
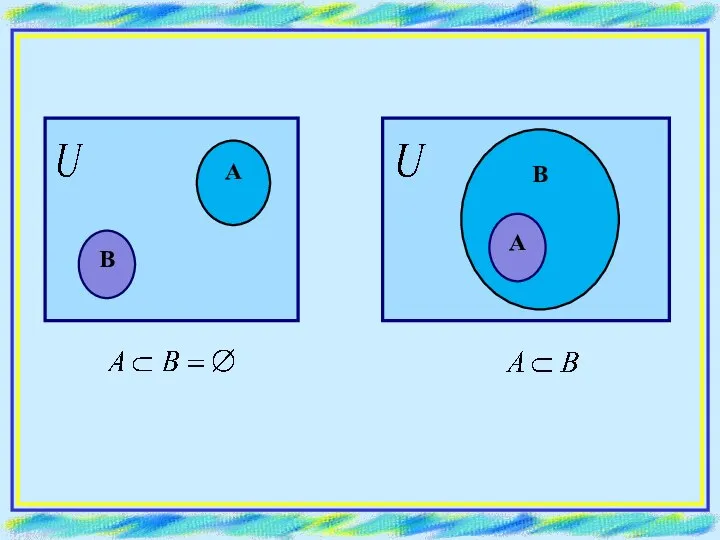
- 5. Множество Ā = U \ A называется дополнением множества А до универсума U А Пусть А
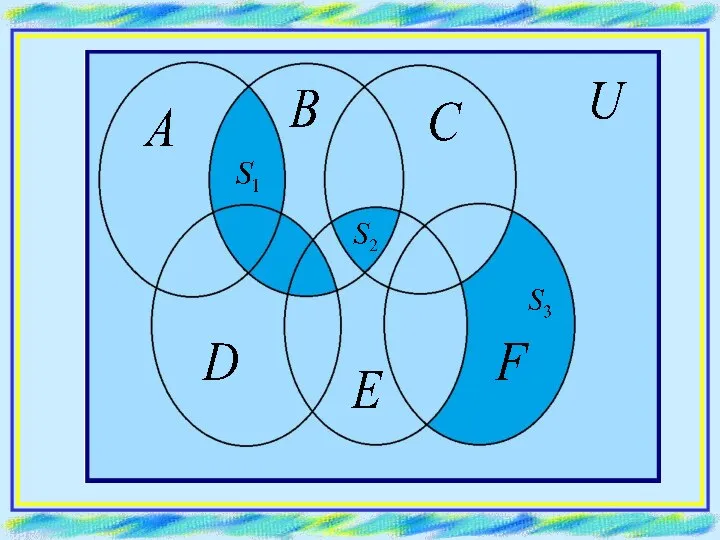
- 9. ПРИМЕР. Пусть элементами множеств являются точки кругов A, B, C, D, E, F, а универсумом U
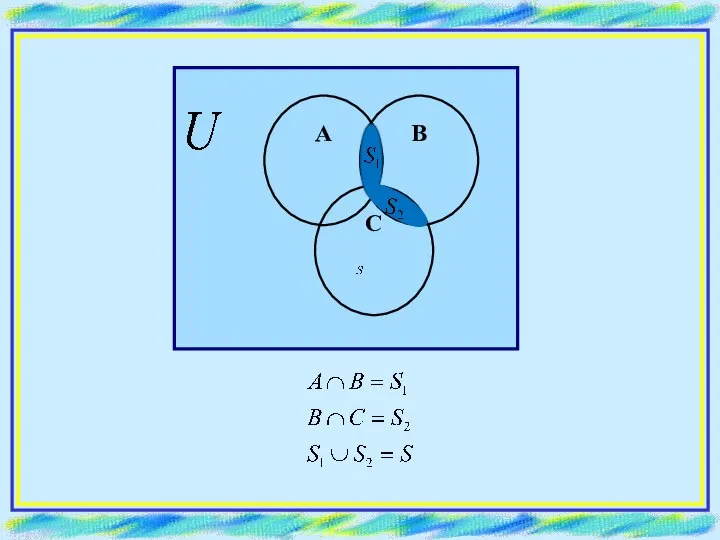
- 11. РЕШЕНИЕ. S1 = (A ∩ B) ∪ (B ∩ D) S2 = B ∩ C ∩
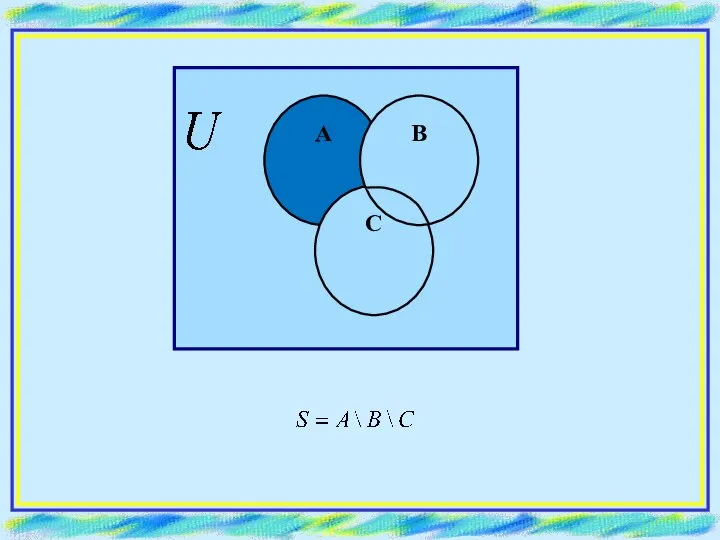
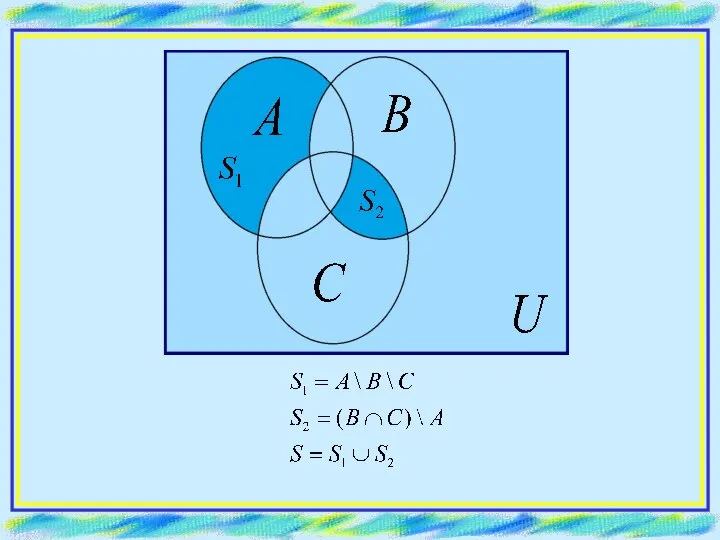
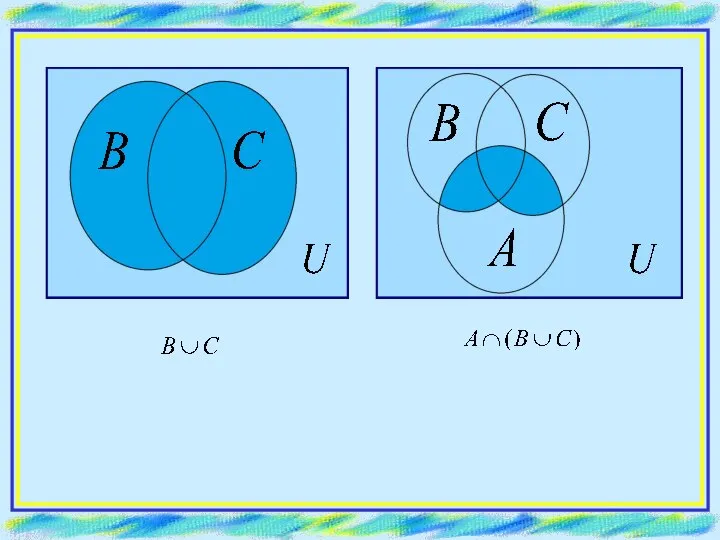
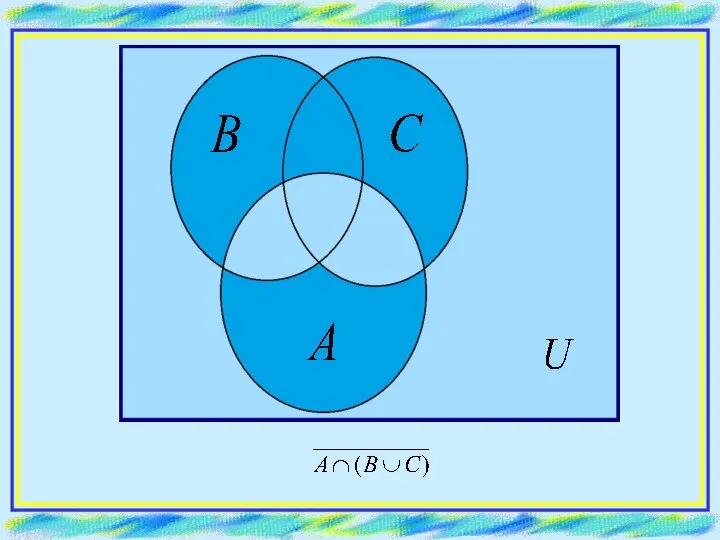
- 12. ПРИМЕР. Отобразить множество:
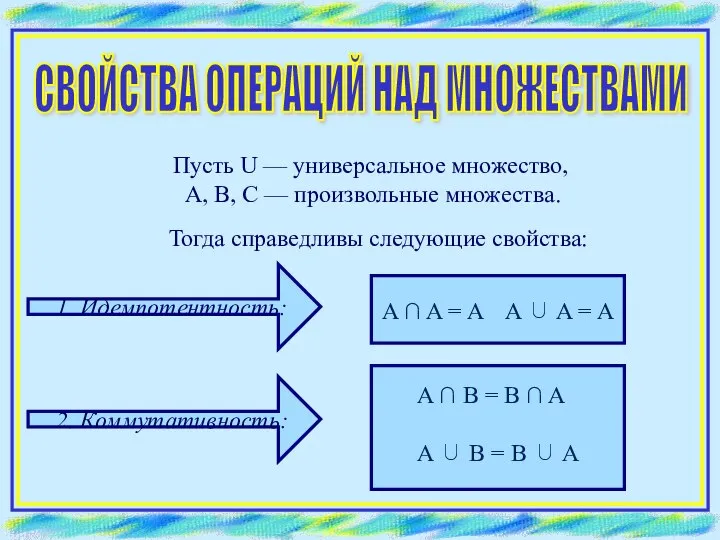
- 15. СВОЙСТВА ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ Пусть U — универсальное множество, A, B, C — произвольные множества. Тогда
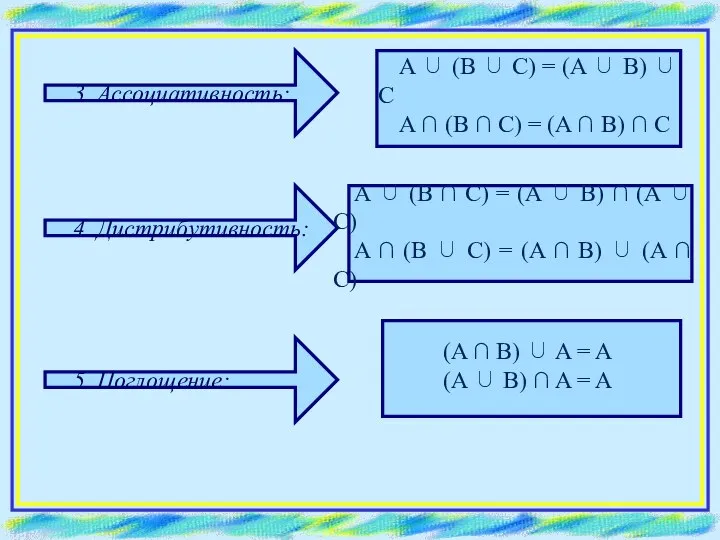
- 16. 3. Ассоциативность: 4. Дистрибутивность: 5. Поглощение:
- 18. Скачать презентацию





 Знакомство с деятельностью Ивана Грозного, через решение математических задач
Знакомство с деятельностью Ивана Грозного, через решение математических задач Сокращённая ДНФ
Сокращённая ДНФ Приёмы умножения числа 2
Приёмы умножения числа 2 Нулевой угловой коэффицент
Нулевой угловой коэффицент Письмо цифр
Письмо цифр Неравенства. Решение линейных неравенств
Неравенства. Решение линейных неравенств Вычисление процентов
Вычисление процентов Бастапқы математикалық көріністерді қалыптастыру
Бастапқы математикалық көріністерді қалыптастыру Действия над обыкновенными дробями. Счет и вычисления
Действия над обыкновенными дробями. Счет и вычисления Теория вероятности. События и испытания
Теория вероятности. События и испытания Статистическая обработка данных в механике. Комбинаторика, теория вероятности
Статистическая обработка данных в механике. Комбинаторика, теория вероятности Действия со степенями. Срезовая работа для 8 класса
Действия со степенями. Срезовая работа для 8 класса Преобразование иррациональных выражений
Преобразование иррациональных выражений Кривая Лоренца. Решение задач
Кривая Лоренца. Решение задач Роль теории коммуникации, теории информации,теории вероятностей
Роль теории коммуникации, теории информации,теории вероятностей Сравнение десятичных дробей
Сравнение десятичных дробей Измерение длины отрезка
Измерение длины отрезка Вимірювальні прибори
Вимірювальні прибори Группировка слагаемых
Группировка слагаемых Наименьшее значение выражения
Наименьшее значение выражения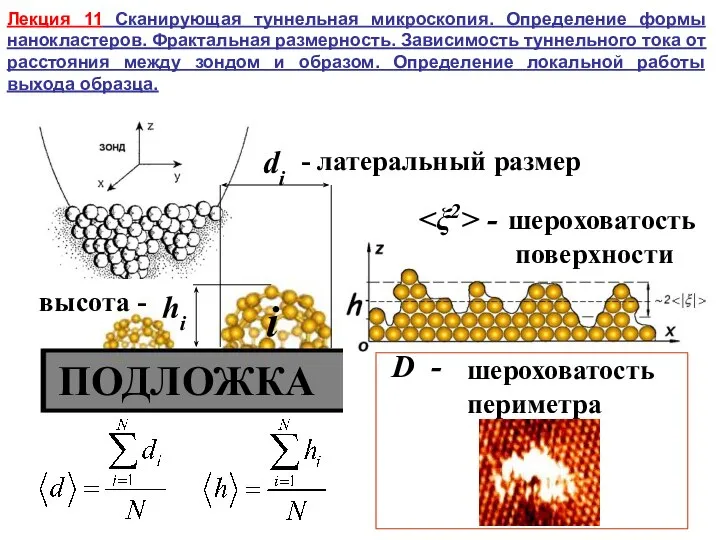 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Связь между координатами вектора и координатами его начала и конца
Связь между координатами вектора и координатами его начала и конца Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Прямоугольный треугольник
Прямоугольный треугольник Степень числа а с натуральным показателем
Степень числа а с натуральным показателем Виды графов
Виды графов Презентация на тему Медиана
Презентация на тему Медиана