Уравнения и неравенства с двумя переменными, содержащие параметр

Определение. Уравнение (неравенство) с параметром – математическое уравнение (неравенство), внешний вид и решение которого зависит от значений одного или нескольких параметров.
Параметр (от греческого рarametron – отмеривающий). В математике, величина, числовые значения которой позволяют видеть определённый элемент из множества элементов того же рода.

Задача.
Решить уравнение: (а2 – 9)х = а + 3
Решение.
Разложим на множители коэффициент перед х
(а – 3)(а + 3) х = а + 3
Если а , то уравнение имеет единственный
корень
Решение простейших уравнений

Задача (продолжение).
Решить уравнение: (а2 – 9)х = а + 3
Решение.
(а – 3)(а + 3) х = а + 3
Если а = 3, то уравнение имеет вид: 0х = 6, уравнение корней не имеет.
Если а = - 3, то уравнение имеет вид: 0х = 0, уравнение имеет множество корней (х € R).
Решение простейших уравнений
Ответ: при а один корень ;
при а = 3 нет корней;
при а = - 3, х € R.

Определение. Уравнение f(x; y) = 0 называется уравнением с двумя переменными.
Определение. Решением уравнения с двумя переменными называется упорядоченная пара чисел (х0; у0), при подстановке которой в уравнение f(x0; y0) = 0, оно обращается в верное равенство.

Пример.
Уравнение: х2 + у2 = 1 имеет бесчисленное множество решений. Решением является любая пара чисел, лежащих на единичной окружности с центром в начале координат.
Уравнение: х2 + у2 = а. Это уравнение с двумя переменными и параметром а.
Решение: При а = 0, уравнение имеет одно
решение (0; 0);
При а < 0, нет решений (сумма двух неотрицательных выражений не может быть отрицательна);
При а > 0, множество решений.

Если подставить знак неравенства х2 + у2 < 1, то решением неравенства будет часть плоскости, лежащей внутри единичной окружности с центром в начале координат.
Вывод: из приведённых примеров видно, что графический способ наиболее понятен.

Пример 1.
Сколько решений имеет система уравнений:
Решение: Строим в одной системе координат оба графика.
Ответ: При а = 0, одно решение (0; 0);
При а > 0, два решения (окружность и парабола будут иметь две точки пересечения).

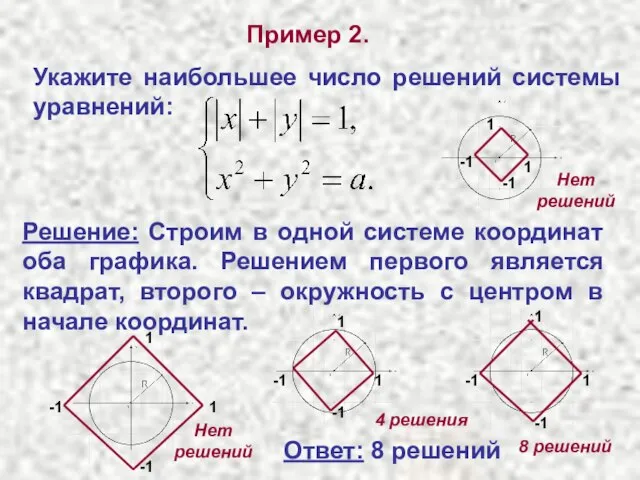
Пример 2.
Укажите наибольшее число решений системы уравнений:
Решение: Строим в одной системе координат оба графика. Решением первого является квадрат, второго – окружность с центром в начале координат.
1
1
-1
-1
-1
-1
1
1
1
1
1
1
-1
-1
-1
-1
Нет решений
Нет решений
4 решения
8 решений
Ответ: 8 решений

Пример 3.
Сколько решений имеет уравнение:|x| + |y| = a?
Решение: Строим в одной системе координат графики левой и правой частей уравнения: графиком уравнения |x| + |y| является квадрат, а графиком уравнения у = а – прямая, параллельная оси ох.
Возможны 3 случая:
бесчисленное множество решений (прямая у = а совпадает со стороной квадрата);
два решения (две точки пересечения);
нет решений (нет точек пересечения).

Пример 4.
Сколько корней имеет уравнение: |х2 – 2х -3| = a, в зависимости от параметра а?
Решение: Строим в одной системе координат графики левой и правой частей уравнения у = |х2 – 2х -3| и у = а.
a < 0
a = 0
0 < a < 4
a = 4
a > 4
Ответ: При а = 0 и a > 4, два корня;
При 0 < а < 4, четыре корня;
При а = 4 три корня;
При а < 0 корней нет.

Работа с учебником.
Стр. 259. Разобрать решение задачи № 1. Выполнить по аналогии стр. 266 № 23.
Опираясь на рассмотренные примеры, выполнить: № 32; № 47(а).

Тренировочные задания

Задание 1.
При каких значениях параметра а, уравнение не имеет корней? Установить соответствие между уравнением и значением параметра.
А. (а – 3)х = а – 2;
В. 3а(а – 2)х = а – 2;
С. (а + 2)2х = а2 – 8.
1. а = – 2;
2. а = 3;
3. а = 0.

Задание 2.
При каких значениях параметра а, уравнение имеет единственный корень? Установить соответствие между уравнением и значением параметра.
А. (а – 5)х = 6;
В. а(х – 3) = а – 5;
С. (а + 3)2х = а.
1. а ǂ – 3;
2. а ǂ 5;
3. а ǂ 3;
4. а ǂ 0.

Задание 3.
При каких значениях параметра р, любое число является корнем уравнения? Установить соответствие между уравнением и значением параметра.
А. р(р – 4)(р + 3)х = 5(4 – р);
В. (р – 2)х = р2 – 4;
С. рх = р(р – 1)(р – 2).
1. р = 4;
2. р = 2;
3. р = 1;
4. р = 0;
5. р = - 3;
6. р = - 2

Задание 4.
При каких значениях параметра а, выполнено неравенство 5|a| > |a|? Выбрать номер правильного ответа.
1. При любом а;
2. При а > 0;
3. При а < 0;
4. При любом а, кроме 0.

Задание 5.
Сколько корней может иметь система уравнений, в зависимости от параметра а? Выбери номера верных ответов.
1. Один;
2. Два;
3. Множество;
4. Не имеет корней.

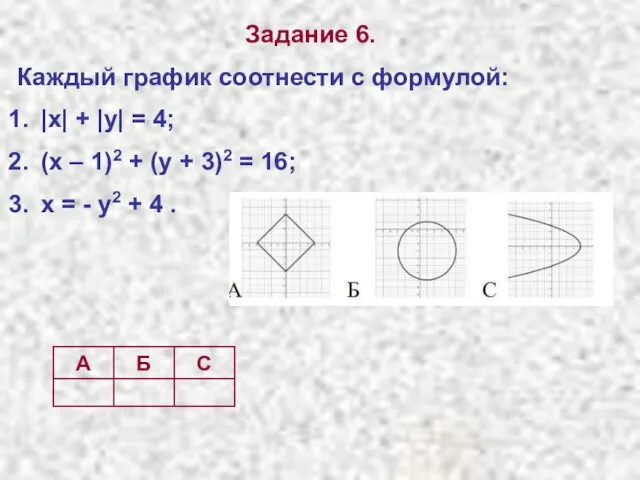
Задание 6.
Каждый график соотнести с формулой:
|x| + |y| = 4;
(x – 1)2 + (y + 3)2 = 16;
х = - y2 + 4 .

Задание 7.
При каком значении параметра а, система уравнений не имеет решений? Выбери номер верного ответа.
1. а = 4;
2. а = - 4;
3. а = - 1;
4. а = 3.

Задание 8.
При каком из графиков изображено решение системы неравенств?