Содержание
- 2. Правила Уравнения называются ЦЕЛЫМИ, если у них левая и правая части являются целыми выражениями (т.е. не
- 3. Надо научиться решать уравнения n-й степени Рn(х)=0 При n=1 имеем линейное уравнение ax +b=0? у которого
- 4. Уравнение n-й степени Рn(х)=0 имеет не более n корней Для 3-й и 4-й степени существуют формулы
- 5. Разложение на множители Замена переменной Графический способ Три основных приёма:
- 6. Пример1. х³+2x²-x-2=0 x²(х+2) – (х+2)=0 (х+2)(x²-1)=0 (х+2)(х-1)(х+1)=0 х=-2; х=-1; х=1
- 7. Пример2. 6х²(x-1)-x²+x-2x+=0 6х²(x-1)-(х²-x)-(2х-2)=0 6х²(x-1)-х(х-1)-2(х-1)=0 (х-1)(6х²-x-2)=0 х=1; х=2/3; х=-1/2
- 8. Кубическое уравнение – алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ax³+bx²+cx+d=0, где a≠0 Заменяя в
- 9. Решение кубического уравнения можно получить с помощью формулы Кардано: Если Если >0, то кубическое уравнение имеет
- 10. Биквадратное уравнение ах +bx²+c=0 4 Решаются заменой переменной у=х² ау²+by+c=0
- 11. Пример3. 4х - 5х² + 1=0 у=х² 4у²-5у+1=0 у=1; у=1/4 х=-1; х=1; х=1/2; х=-1/2 4
- 12. Пример4. (х²-2x)²-4(x²-2x)+3=0 у=(x²-2x) у²-4у+3=0 у=1; у=3 х²-2х=1 х²-2х=3 х²-2х-1=0 х²-2х-3=0 х=1-√2; х=1+√2; х=-1; х=3
- 13. Пример5. (х²+4х+3)(х²+4х+1)=48 у= (х²+4х+1) у(у+2)=48 у²+2у-48=0 у=-8 у=6 х²+4х+1=-8 х²+4х+1=6 х²+4х+9=0 х²+4х-5=0 корней нет х=-5; х=1
- 14. Пример 6. (х-1)(х+1)(х+3)(х+5)=105 При решении этой задачи важно сообразить, что (х-1)(х+5)=х²+4x-5, (х+1)(х+3)= х²+4x+3. Поэтому изменив порядок
- 15. Пример 7. (х²+3x-8)²+2x(х²+3x-8)-3х²=0 Многочлен, который стоит в левой части уравнения, легко свести к однородному многочлену двух
- 16. y²+2xy-3x²=0 D= у= у= у=-3х и у=х.
- 17. Возвращаясь к переменной х, имеем два уравнения: х²+3x-8=-3х и х²+3x-8=х (корни х=-3- √17 и х=-3+ √17)
- 18. Решите уравнение: №272(а) y³-6y=0 y(y²-6)=0 Ответ: у=0, у=-√6, y=√6
- 19. Решите уравнение: №272(д) 9х³-18x²-x+2=0 (9х³-18x²)-(x-2)=0 9x²(х-2)-(x-2)=0 (x-2)(9x²-1)=0 (x-2)(3х-1)(3х+1)=0 Ответ: х=-1/3, х=1/3, х=2
- 20. Решите уравнение: №276(а) (2х² +3)² – 12(2х²+3)+11=0 Заменим (2х²+3)=h, имеем h²-12h+1=0
- 21. Решите уравнение: №278(а) х – 5х² -36=0 4
- 22. Теорема Безу.
- 23. Преподавал математику в Училище гардемаринов (1763) и Королевском артиллерийском корпусе (1768). Основные его работы относятся к
- 24. Любой многочлен R(x) можно представить в виде: P(x)= (х-а) ∙Q(х) + r, где r =P(a) Пример
- 25. Теорема Безу. Если уравнение а х + a x + … + a x+a = 0,
- 26. х³-8х²+19х-12=0 Свободный член – 12 имеет делители ±1, ±2, ± 3, ±4, ±6, ±12. При x=1
- 27. Решение задач. 1) Решить уравнения: а) х³-3х²-4х+12=0, б) х³+4х²+5х+2=0, в) х +4х³+х²-12х-12=0, г) х +4х³-х²-16х-12=0. 4
- 28. Решим уравнение с помощью теоремы Безу: х³-6х²+11х-6=0
- 29. Можно не делить многочлен на двучлен, а воспользоваться схемой Горнера Метод назван в честь Уильяма Джоржа
- 30. Решить уравнение: х³-5х+4=0 х³-3х+2=0 4: на +/-1;+/-2; +/-4 х³-5х+4=(х-1)(х²+х-4)=0
- 31. Возвратные уравнения Рассмотрим уравнения: x³-3x²-3x+1=0 3х -7х³+x²-7x+3=0 -х³+5x²+5x-1=0 Все три уравнения объединяет то, что коэффициенты равноотстоящие
- 32. КАК РЕШАТЬ? ?
- 33. Рассмотрим методы решения возвратных уравнений 3-ей и 4-ой степени. В общем виде возвратное уравнение 3-ей степени
- 34. Тогда уравнение (3) примет вид полученное уравнение равносильно совокупности двух уравнений , , решая первое уравнение
- 35. Пример решения кубического уравнения заменой переменных Пример. Решить уравнение Решение. Сначала приведем уравнение к трехчленному виду.
- 36. Тогда поскольку то уравнение примет вид Далее из получаем Заметим, что такое же, как и в
- 37. Рассмотрим возвратное уравнение 4-ой степени (4) Так как , то не является корнем этого уравнения. Поэтому,
- 38. Полученное уравнение можно решить уже знакомым нам методом замены переменной. Пусть ,тогда ,откуда получаем, что и
- 39. Решив это уравнение, найдем его корни t1и t2 Теперь чтобы найти корни уравнения (4) необходимо решить
- 40. Решение. Имеем возвратное уравнение 4-ой степени. Разделим обе части уравнения на х², проведем группировку слагаемых и
- 41. Решая это уравнение, получим и Для нахождения корней первоначального уравнения решим дробно-рациональные уравнения решение которых сводится
- 42. Решить уравнения: 5х³-4x²-4x+5=0
- 43. Решить уравнения: 2x -5x³+4x²-5x+2=0 4
- 44. Однородные уравнения Одноро́дным уравнением n-й степени, называется дифференциальное уравнение вида: Такое уравнение заменой сводится к алгебраическому
- 45. Примеры однородных уравнений: sin х — cos х = 0, 3(х²+5)²+4(х²+5)(х-7)-7(х-7)²=0 (х-3)+4(х+3)=5(х²-9)² ↔ (х-3)+4(х+3)=5(х-3)²(х+3)² 4 4
- 46. (х-3)+4(х+3)=5(х-3)²(х+3)² Разделим обе части уравнения на (х-3) и сделаем замену t=((х+3):(х-3))² Получим равносильное уравнение: 1+4t²=5t, корни
- 47. Итоги урока: Какие уравнения называются уравнениями высоких порядков? Что значит решить уравнение? Сколько корней может иметь
- 49. Скачать презентацию










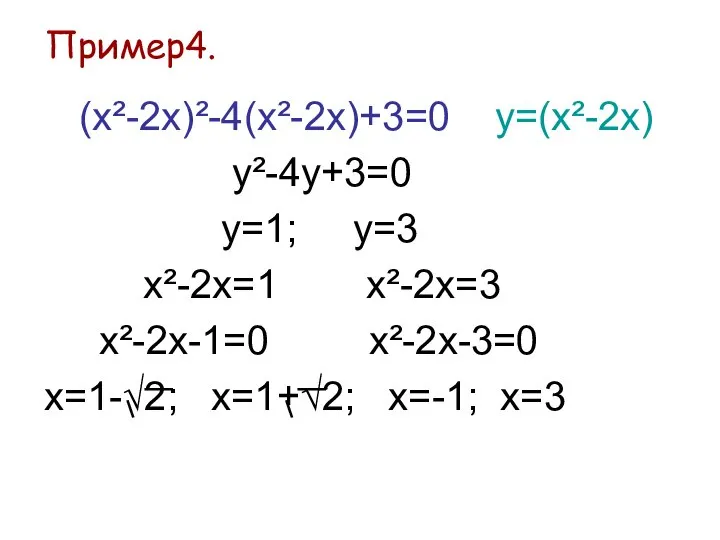



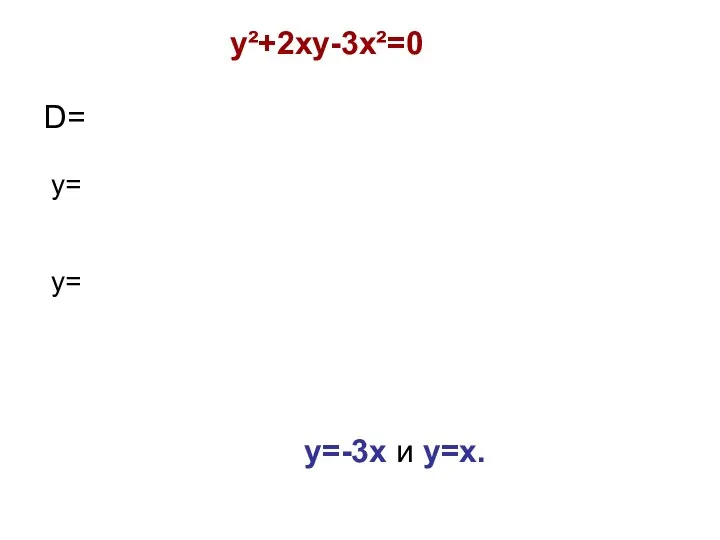






























 Анализ представленности геометрического материала в учебнике М.И. Моро (1-4 класс)
Анализ представленности геометрического материала в учебнике М.И. Моро (1-4 класс) Симметрия в пространстве
Симметрия в пространстве Приобретать знания- храбрость, приумножать их – мудрость, а умело приумножать- великое искусство.
Приобретать знания- храбрость, приумножать их – мудрость, а умело приумножать- великое искусство. Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Область определения функции. С/Р
Область определения функции. С/Р Презентация на тему Квадрат
Презентация на тему Квадрат  повторение 8 класса
повторение 8 класса Анализ контрольной работы
Анализ контрольной работы Обучение для выполнения НИР 5 курса. Занятие №2
Обучение для выполнения НИР 5 курса. Занятие №2 Презентация на тему Метод параллельного проектирования
Презентация на тему Метод параллельного проектирования  Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Вычитание в пределах 20 с переходом через разряд. Тренажер
Вычитание в пределах 20 с переходом через разряд. Тренажер Пифагор Самосский
Пифагор Самосский Прикладная математика. Лекция 10. Контрольная работа
Прикладная математика. Лекция 10. Контрольная работа Презентация на тему: Турнир смекалистых
Презентация на тему: Турнир смекалистых Вычитание смешанных чисел
Вычитание смешанных чисел Предел числовой последовательности
Предел числовой последовательности Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Вычитание смешанных чисел
Вычитание смешанных чисел Тест № 2 по теме Функция
Тест № 2 по теме Функция Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Системы принятия решений. Алгоритмы оптимизации
Системы принятия решений. Алгоритмы оптимизации Презентация на тему Сравнение трехзначных чисел (3 класс)
Презентация на тему Сравнение трехзначных чисел (3 класс)  Логика высказываний. Таблица истинности логических союзов
Логика высказываний. Таблица истинности логических союзов Действия с дробями
Действия с дробями Понятие функции. Свойства функций
Понятие функции. Свойства функций Составление краткой записи и решение задач
Составление краткой записи и решение задач Презентация на тему Тренажер по математике 2 класс
Презентация на тему Тренажер по математике 2 класс