user_file_5edd0051b6aa7

Цели урока:
изучить взаимное расположение прямой
и плоскости в пространстве;
ввести понятие параллельности прямых
и плоскостей в пространстве.
Задачи:
расширение кругозора знаний,
развитие пространственного
мышления.

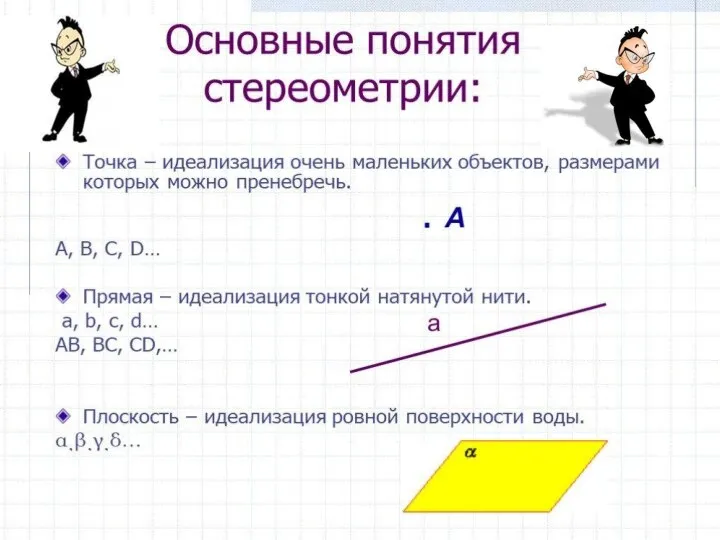
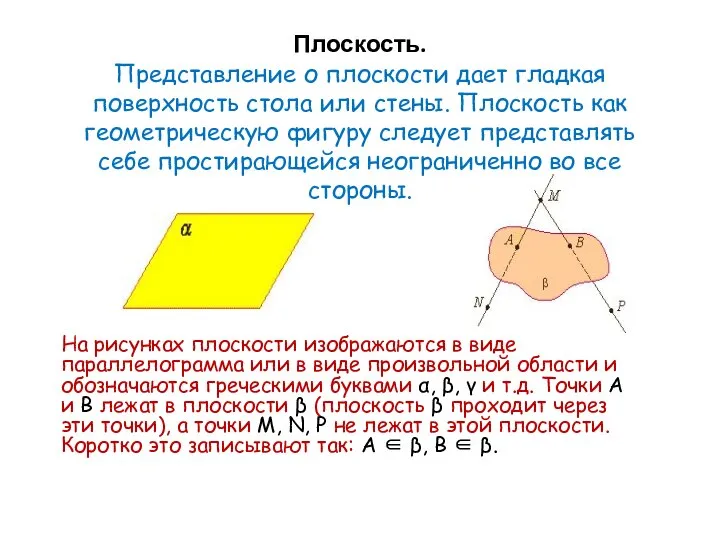
Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β.

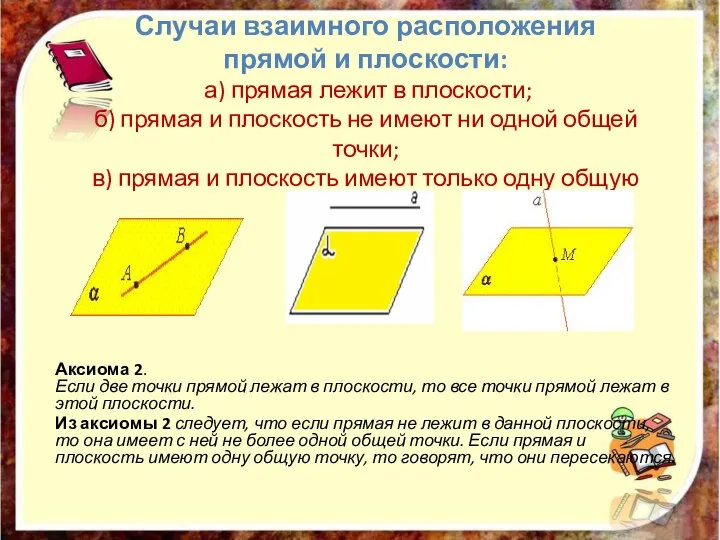
Случаи взаимного расположения
прямой и плоскости:
а) прямая лежит в плоскости;
б) прямая и плоскость не имеют ни одной общей точки;
в) прямая и плоскость имеют только одну общую точку.
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

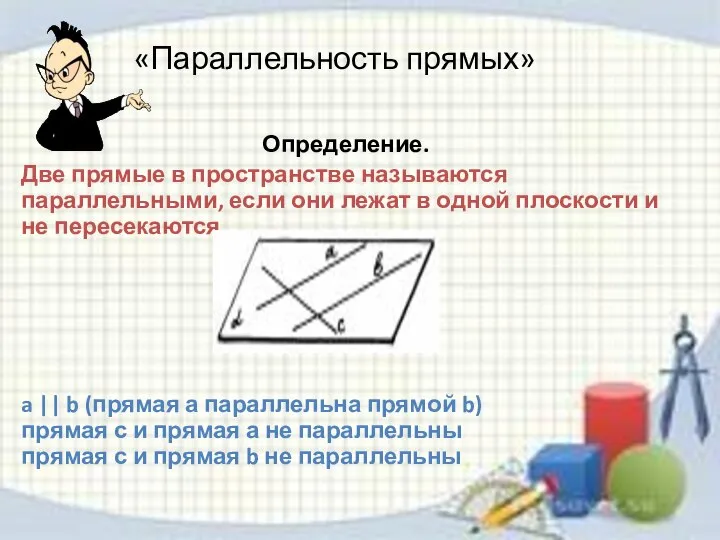
«Параллельность прямых»
Определение.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
a || b (прямая а параллельна прямой b)
прямая с и прямая а не параллельны
прямая с и прямая b не параллельны

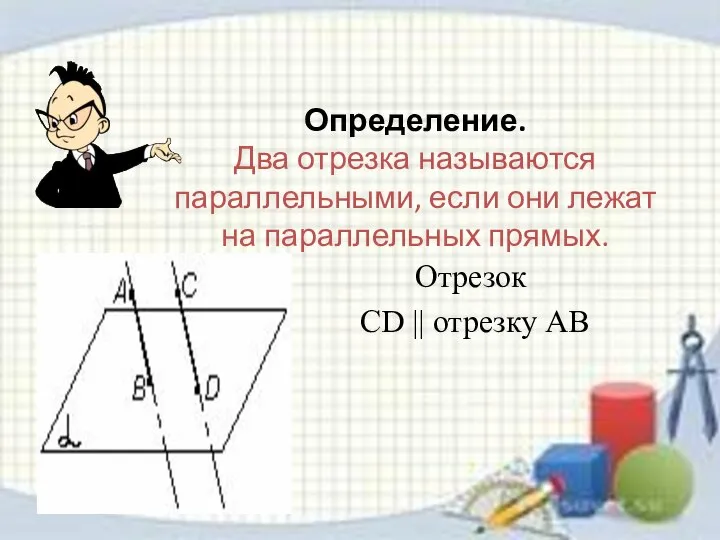
Определение.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Отрезок
СD || отрезку АВ

Теорема
о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

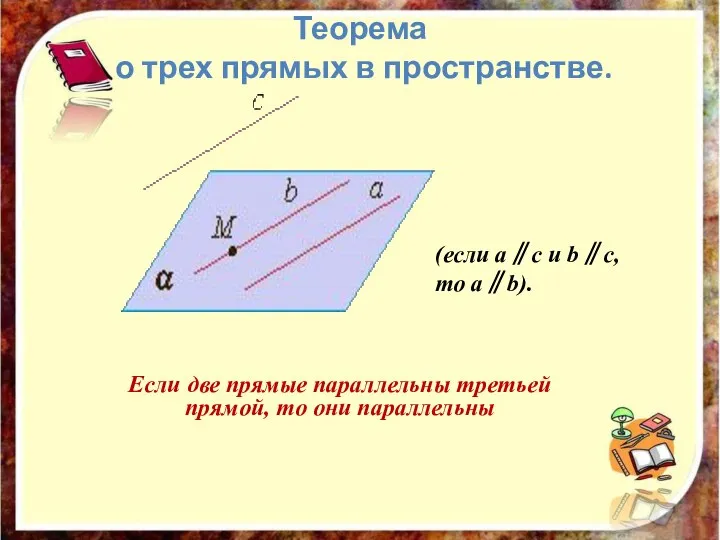
Теорема
о трех прямых в пространстве.
Если две прямые параллельны третьей прямой, то они параллельны
(если a∥c и b∥c,
то a∥b).

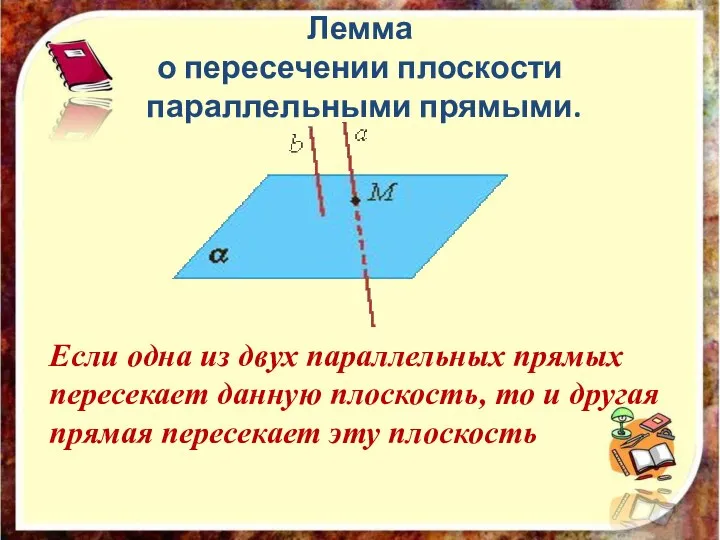
Лемма
о пересечении плоскости
параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость

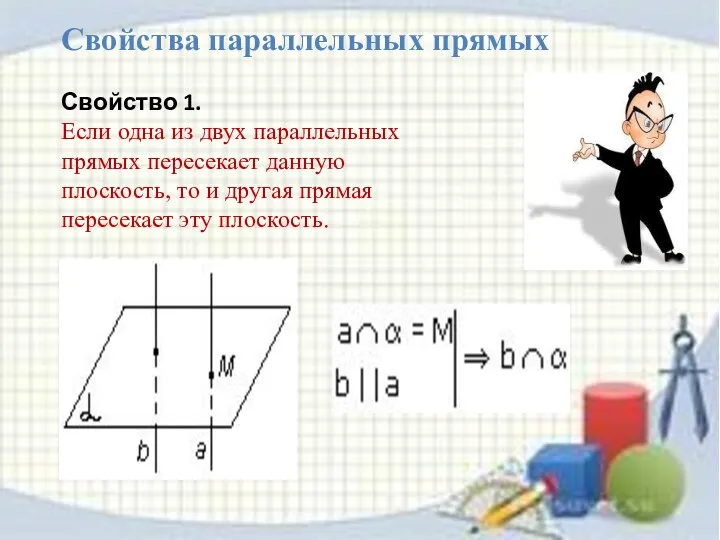
Свойства параллельных прямых
Свойство 1.
Если одна из двух параллельных
прямых пересекает данную
плоскость, то и другая прямая
пересекает эту плоскость.

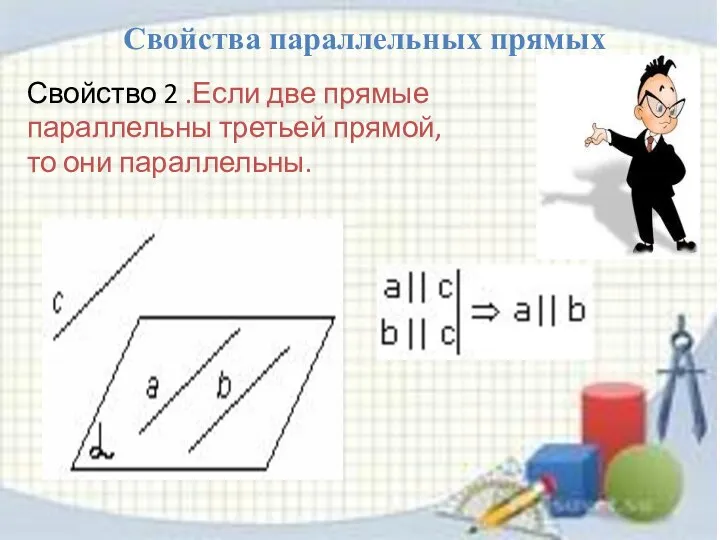
Свойство 2 .Если две прямые
параллельны третьей прямой,
то они параллельны.
Свойства параллельных прямых

Взаимное расположение
прямых в пространстве
Пересекающиеся прямые:
лежат в одной плоскости, имеют одну общую точку.

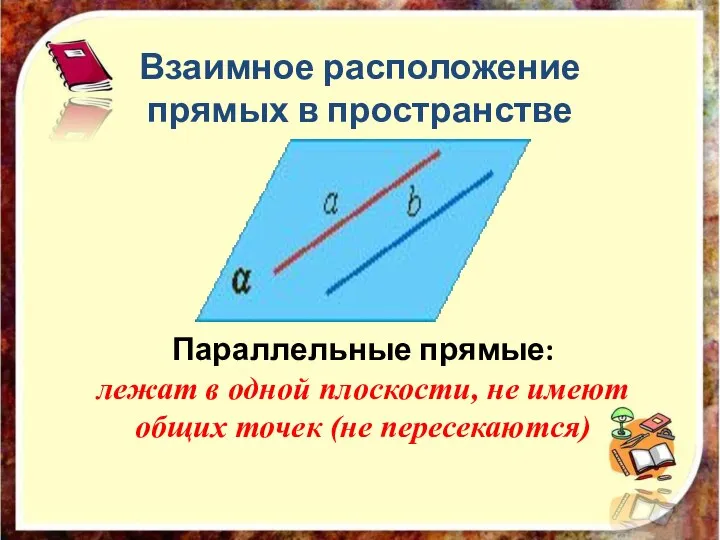
Взаимное расположение
прямых в пространстве
Параллельные прямые:
лежат в одной плоскости, не имеют общих точек (не пересекаются)

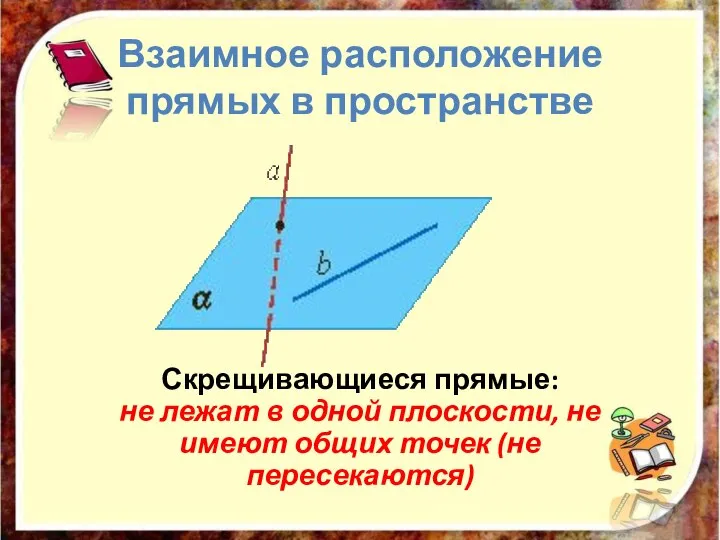
Взаимное расположение
прямых в пространстве
Скрещивающиеся прямые:
не лежат в одной плоскости, не имеют общих точек (не пересекаются)

Признак скрещивающихся прямых.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
a и b-
скрещивающиеся
прямые

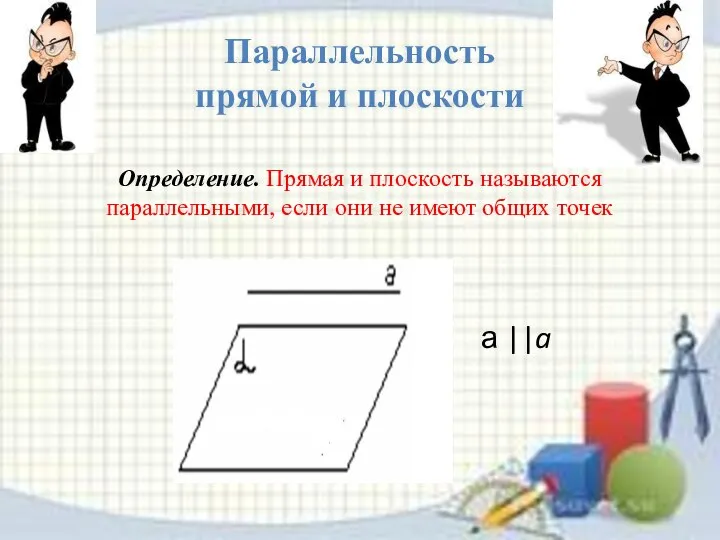
Параллельность
прямой и плоскости
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек
а ||a

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Признак параллельности
прямой и плоскости.

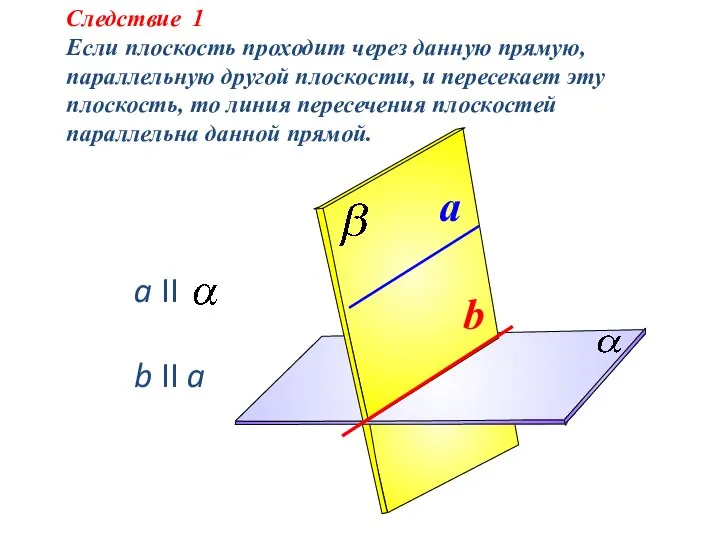
b II a
Следствие 1
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

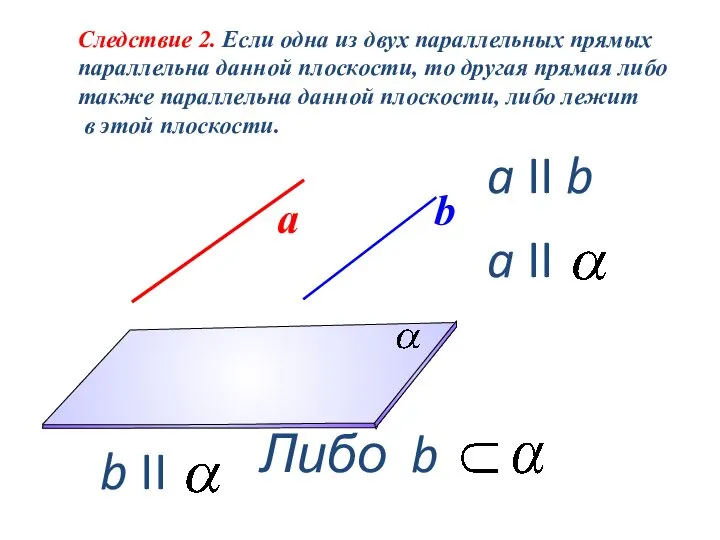
Следствие 2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо
также параллельна данной плоскости, либо лежит
в этой плоскости.
a II b

Параллельность прямой и плоскости
Следствие 3. Если одна из двух параллельных прямых параллельна данной плоскости, а другая прямая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости.

Ответить на вопросы
1) Как могут располагаться прямая и плоскость в пространстве?
2) В каких сучаях прямая и плоскость будут параллельны?
3) В каких случаях отрезок и плоскость будут параллельны?
4) Сколько плоскостей можно провести через прямую и параллельную плоскость?

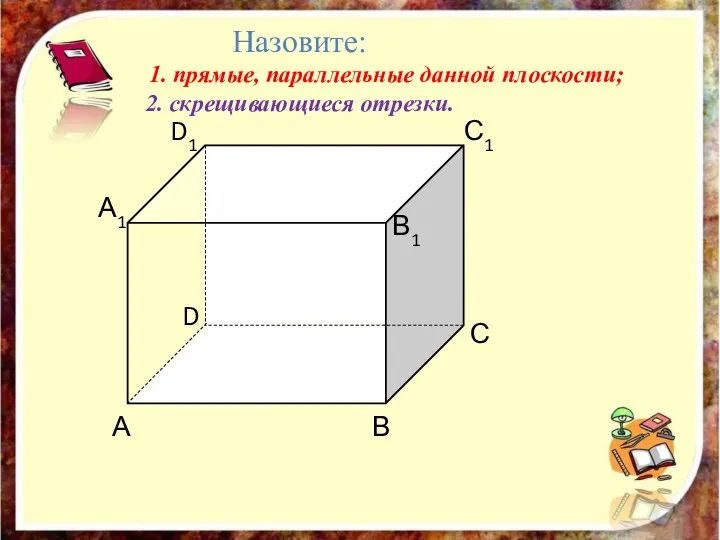
А
В
С
D
D1
С1
В1
А1
Назовите:
1. прямые, параллельные данной плоскости;
2. скрещивающиеся отрезки.