В мире рациональных уравнений

Приобретенные при изучении дополнительной научной литературы навыки в дальнейшем позволят решать достаточно широкий круг текстовых задач, что является актуальным при изучении математики и смежных дисциплин.
систематизировать методы решения рациональных уравнений и показать их применение при решении нестандартных уравнений.
Актуальность исследования
Цель исследования:
Введение

отобрать научную литературу по данной теме;
научиться решать квадратные уравнения различными методами;
познакомиться с понятием симметрических, возвратных и однородных уравнений;
изучить методы решения рациональных уравнений;
научиться выбирать оптимальные способы решения рациональных уравнений при решении нестандартных задач по математике.
Объект исследования:
рациональные уравнения
изучение приёмов решения нестандартных задач, основанных на использовании основных методов решения рациональных уравнений
Задачи:
Введение
Предмет исследования:

Известный арабский математик Ал-Хорезми в своей книге «Ал-джабар» описал способы решения различных уравнений, в том числе и уравнений
высших степеней.
Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней уравнений.
Из истории рациональных уравнений

Рациональное выражение с одной переменной – это алгебраическое выражение, составленное из чисел и переменной x с помощью операций сложения, вычитания, умножения, деления и возведения в целую степень.
Уравнение f(x) = g(x) называется рациональным, если f(x) и g(x) – рациональные выражения.
Если f(x) и g(x) – целые выражения, то уравнение называют целым.
Рациональное уравнение f(x) = g(x) называется дробным, если хотя бы одно из выражений f(x) или g(x) является дробным.
Основные понятия

Простейшие преобразования. Достаточно выполнить обычные упрощения: приведение к общему знаменателю, приведение подобных членов и т.д.
2. Подстановка. Иногда при решении рациональных уравнений имеет смысл ввести новую переменную, заменив ею некое повторяющееся рациональное выражение.
3. Распадающееся уравнение. Рациональное уравнение называется распадающимся, если его можно представить в виде P(x)Q(x) = 0, где P(x) и Q(x) – целые рациональные функции.
Методы решения рациональных уравнений

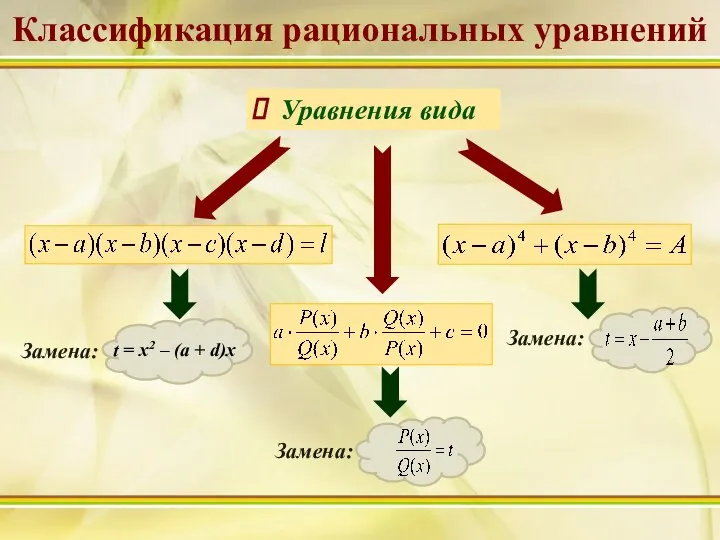
Биквадратное уравнение:
Однородное уравнение 2-ого порядка:
Симметрическое уравнение 4-ого порядка:
Возвратное уравнение 4-ого порядка:
Уравнение вида:
Классификация рациональных уравнений

Уравнения вида
Классификация рациональных уравнений

Вернёмся к замене:
Решение нестандартных уравнений с использованием особых приемов
Решение.
Приём почленного деления

Решение нестандартных уравнений с использованием особых приемов
Решение.
Приём выделения квадрата двучлена
Корней нет.

В ходе исследования обобщены научные сведения по теме «Рациональные уравнения»:
Результаты исследования
приведена классификация рациональных уравнений;
сформулированы основные понятия, связанные с симметрическими, возвратными и однородными уравнениями;
рассмотрены основные способы решения рациональных уравнений;
выявлены приёмы, позволяющие понизить степень уравнения и тем самым упростить процесс решения;

задействовано большое количество математической литературы, освоение которой, позволило повысить уровень знаний;
изучены различные способы решения квадратных уравнений;
приобретены навыки решения рациональных уравнений, которые в дальнейшем могут быть использованы при изучении математики в старших классах и подготовке к математическим олимпиадам и основному государственному экзамену;
ЗАКЛЮЧЕНИЕ
При работе над темой: