Приведение уравнений фигур к каноническому виду при помощи квадратичных форм

Теорема. При невырожденном линейном преобразовании матрица квадратичной формы принимает вид
Теорема.
Собственные векторы, соответствующие различным собственным значениям симметрической матрицы ортогональны.

Говорят, что квадратичная форма имеет канонический вид, если она содержит только квадраты переменных.
Матрица канонической квадратичной формы является диагональной.
Пример.

Теорема. Любая квадратичная форма, с помощью невырожденного преобразования переменных может быть приведена к каноническому виду.

п.2. Применение квадратичных форм для исследования кривых второго порядка.
Рассмотрим квадратичную форму
Канонический вид
Пусть кривая второго порядка задана уравнением

Если
то кривая имеет эллиптический вид;
если
то кривая имеет гиперболический вид;
если
то кривая имеет параболический вид.

Пример. Определить вид кривой
Решение. Составим матрицу
Так как
то кривая имеет эллиптический вид.

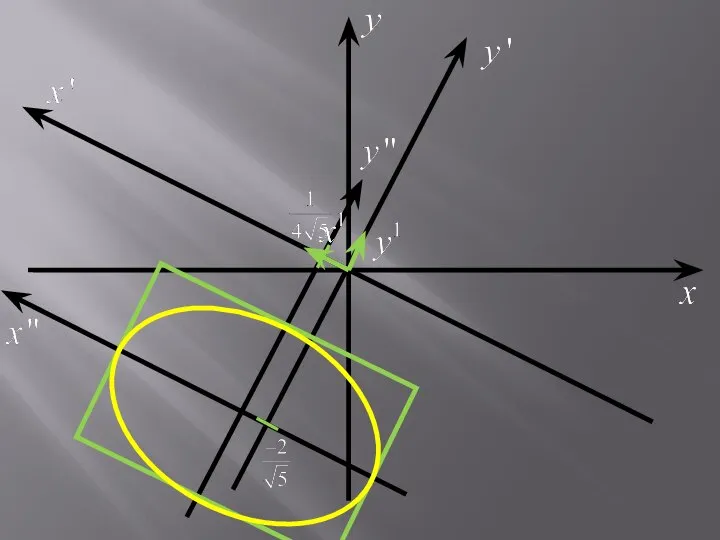
Пример. Привести к каноническому виду уравнение кривой
Сделать рисунок.
Решение. Обозначим
Матрица этой квадратичной формы имеет вид
Составим характеристическое уравнение

Собственные числа:
Найдем собственные векторы.
Пусть
тогда

— собственные векторы, соответствующие собственному числу
Поэтому
Нормируем эти векторы:

Пусть
тогда
Поэтому
— собственные векторы, соответствующие собственному числу

Нормируем эти векторы:

Матрица преобразования координат (матрица поворота):
Формулы преобразования осей координат

Подставив в уравнение данной кривой выражения для x и y
Так как с помощью указанного преобразования координат квадратичная форма приводится к каноническому виду, то получим

Выделим полные квадраты

Подставим
Выполним параллельный перенос по формулам

Окончательно получим
— эллипс с полуосями

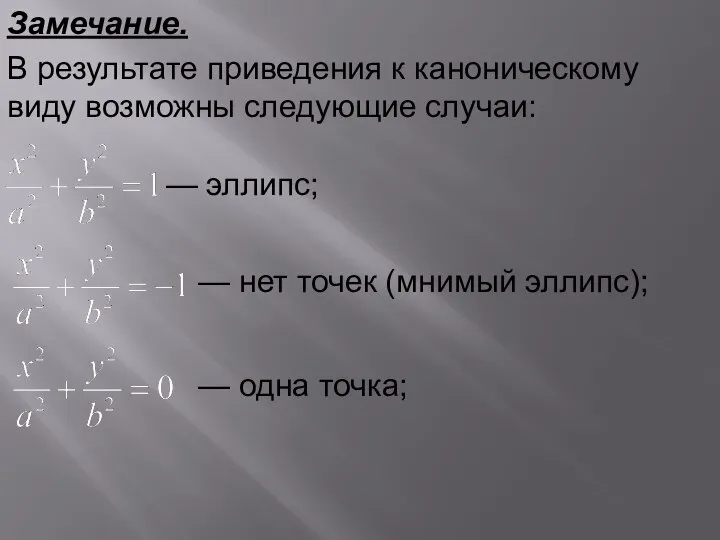
Замечание.
В результате приведения к каноническому виду возможны следующие случаи:
— эллипс;
— нет точек (мнимый эллипс);
— одна точка;

— гипербола с действительной осью Ox;
— пара пересекающихся прямых;
— гипербола с действительной осью Oy;

— парабола (любые варианты);
— пара параллельных прямых;
— нет точек (пара мнимых параллельных прямых);
— одна прямая.