Содержание
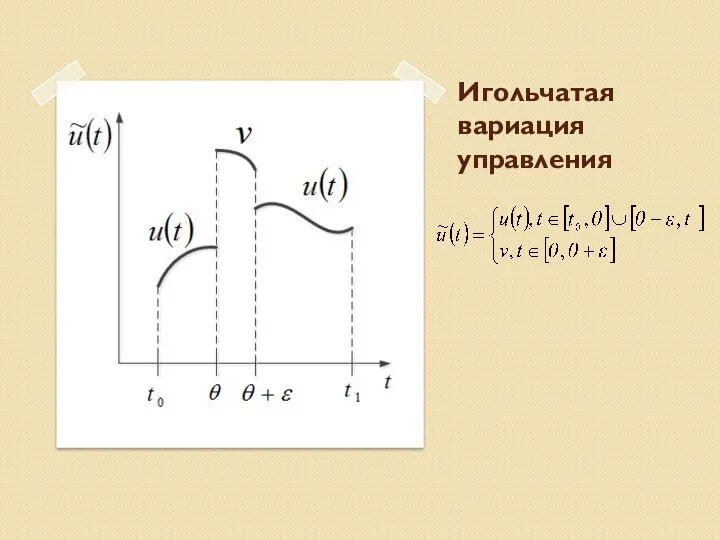
- 2. Игольчатая вариация управления
- 4. 1) 2) 3)
- 6. -оптимальное управление -допустимое управление
- 7. ТЕОРЕМА Принцип максимума Понтрягина Пусть является оптимальным управлением простейшей и при этом является решением системы уравнений
- 8. АЛГОРИТМ Строится получаем Находим решение системы Подставляем найденные в
- 9. Изменение задачи поиска максимума с помощью принципа Понтрягина в зависимости от граничных условий Терминальная задача управления
- 10. Изменение задачи поиска максимума с помощью принципа Понтрягина в зависимости от граничных условий Терминальная задача управления
- 11. Изменение задачи поиска максимума с помощью принципа Понтрягина в зависимости от граничных условий Терминальная задача управления
- 12. Пример
- 13. Пример
- 15. Скачать презентацию
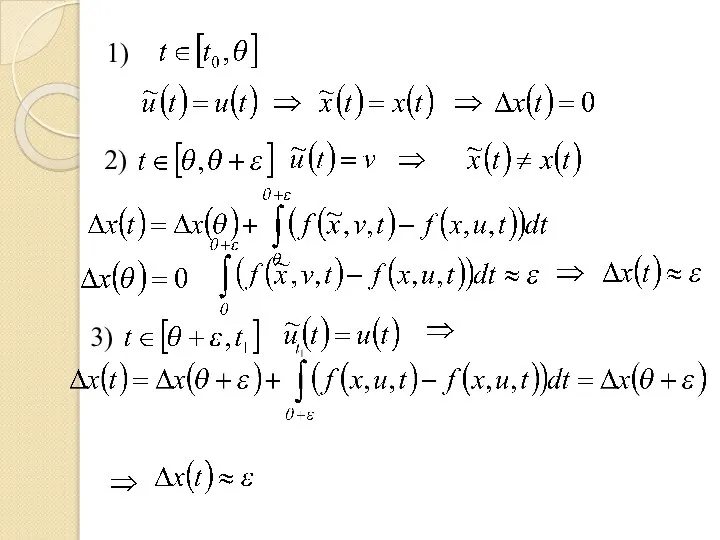








 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц  Консультація до іспиту ТМДМ
Консультація до іспиту ТМДМ Презентация на тему Геометрические тела. Многогранники
Презентация на тему Геометрические тела. Многогранники  Признаки равенства треугольников
Признаки равенства треугольников Математический марафон
Математический марафон Функция. График функции
Функция. График функции Задачи на разрезание
Задачи на разрезание Иррациональные неравенства
Иррациональные неравенства Четырёхугольники. Задачи на готовых чертежах
Четырёхугольники. Задачи на готовых чертежах Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Параллелограмм
Параллелограмм Уравнение плоскости
Уравнение плоскости Решение тригонометрических уравнений sin а
Решение тригонометрических уравнений sin а Имитационное моделирование
Имитационное моделирование Вычитание смешанных чисел. 5 класс
Вычитание смешанных чисел. 5 класс Метод рекуррентных соотношений
Метод рекуррентных соотношений Задача по математике (1 класс, задание 15)
Задача по математике (1 класс, задание 15) ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Свойства корня степени n
Свойства корня степени n Владимир Модестович Брадис и его замечательные таблицы
Владимир Модестович Брадис и его замечательные таблицы Арксинус. Решение уравнения Sin t = a
Арксинус. Решение уравнения Sin t = a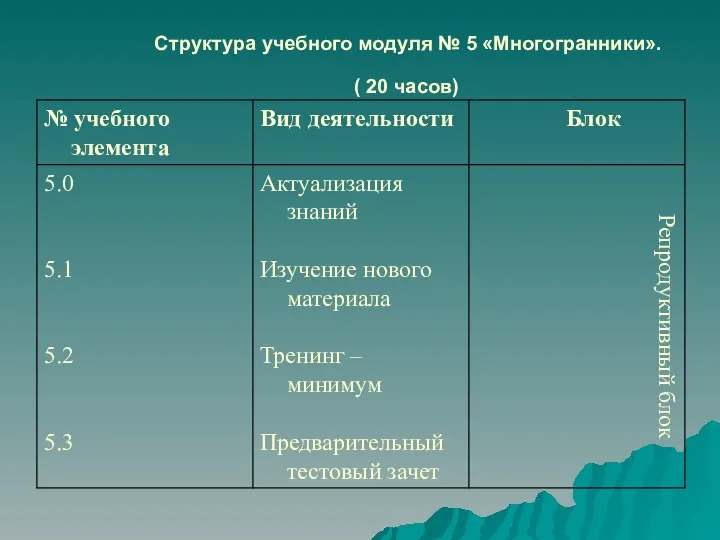 Структура учебного модуля № 5 Многогранники. ( 20 часов)
Структура учебного модуля № 5 Многогранники. ( 20 часов) Презентация на тему Звездчатые многогранники
Презентация на тему Звездчатые многогранники  Функции у=|x| и ей график
Функции у=|x| и ей график Стационарный режим теплообмена с фазовым переходом
Стационарный режим теплообмена с фазовым переходом Прямоугольник
Прямоугольник