Содержание
- 2. Уравнение плоскости в отрезках Если y = 0, z = 0 , то x = a
- 3. Задача 1. Дано: M0 (1, – 5, 6) ; Найти: уравнение плоскости, проходящей через т. M0
- 4. Задача 2. Даны две плоскости: 2x + 3y – 2z – 4 = 0 (1) 13x
- 5. Задача 3. Даны две плоскости: 6x + 4y – 14z + 16 = 0 (1) 3x
- 6. Задача 4. Даны две плоскости: x – z = 0 ; y – z = 0
- 8. Скачать презентацию





 Нарушение осанки и плоскостопие
Нарушение осанки и плоскостопие Тождественные преобразования
Тождественные преобразования Уровень и отвес
Уровень и отвес Делимость чисел. НОД
Делимость чисел. НОД Первый признак равенства треугольников
Первый признак равенства треугольников Игры с природой. Лекция 2
Игры с природой. Лекция 2 Применение математики в банковском деле
Применение математики в банковском деле Геометрия и искусство
Геометрия и искусство Задачи с ветвлением. 8 класс
Задачи с ветвлением. 8 класс Геометрия Евклида
Геометрия Евклида Деление с остатком. Решение задач
Деление с остатком. Решение задач Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Метод простой итерации. Метод дихотомии
Метод простой итерации. Метод дихотомии Решение задач с помощью теоремы Пифагора
Решение задач с помощью теоремы Пифагора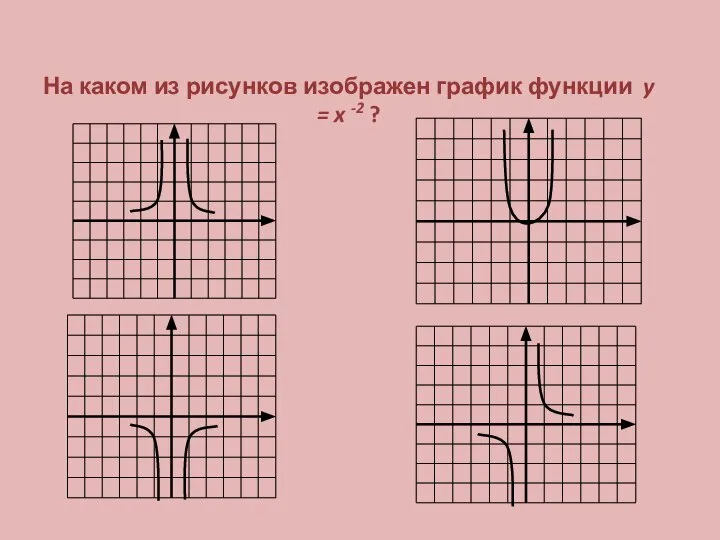 Степенная функция
Степенная функция Характеристики вычислительных систем, представленных в виде моделей СМО
Характеристики вычислительных систем, представленных в виде моделей СМО Сложи вида +2,+3
Сложи вида +2,+3 Упражнения по планиметрии на готовых чертежах. VII класс
Упражнения по планиметрии на готовых чертежах. VII класс Математическая викторина
Математическая викторина Числа от 1 до 10. Сложение и вычитание. Урок 2
Числа от 1 до 10. Сложение и вычитание. Урок 2 Устный счет. 3 класс
Устный счет. 3 класс Прямоугольный треугольник . Решение задач
Прямоугольный треугольник . Решение задач многогранники
многогранники История возникновения геометрии как науки
История возникновения геометрии как науки Математика для родителей
Математика для родителей Система уравнений. Решение систем способом сложения
Система уравнений. Решение систем способом сложения Решение задач с помощью уравнений
Решение задач с помощью уравнений Презентация на тему Математическая сказка "Гуси лебеди" 3 класс
Презентация на тему Математическая сказка "Гуси лебеди" 3 класс