Векторная алгебра

2. ВЕКТОРНАЯ АЛГЕБРА
2.1 Векторы, общие понятия
2.2 Скалярное произведение векторов
2.3 Векторное произведение векторов
2.4 Смешанное произведение векторов

2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Вектором (или свободным вектором) называется направленный отрезок т.е. отрезок прямой с указанием точек начала и конца.
Обозначение: или .
Расстояние от начала вектора до его конца называется длиной или модулем вектора. Обозначение: или .
Вектор, длина которого равна единице, называется единичным вектором или ортом.
Вектор, начало и конец которого совпадают, называется нулевым.
Обозначение: .
Нулевой вектор не имеет определённого направления и имеет длину, равную нулю.

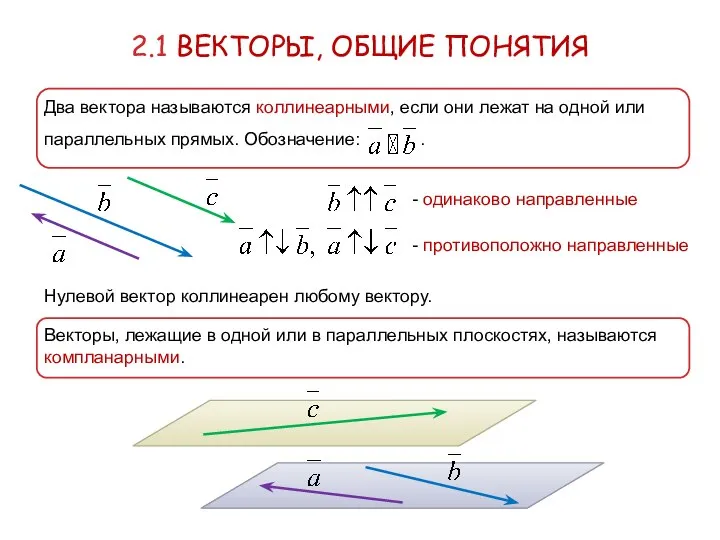
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Два вектора называются коллинеарными, если они лежат на одной или параллельных прямых. Обозначение: .
Векторы, лежащие в одной или в параллельных плоскостях, называются компланарными.
- одинаково направленные
- противоположно направленные
Нулевой вектор коллинеарен любому вектору.

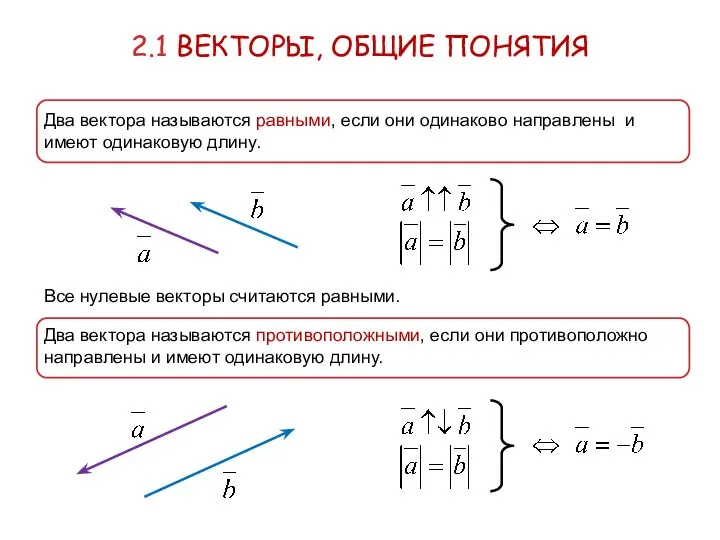
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Два вектора называются равными, если они одинаково направлены и имеют одинаковую длину.
Два вектора называются противоположными, если они противоположно направлены и имеют одинаковую длину.
Все нулевые векторы считаются равными.

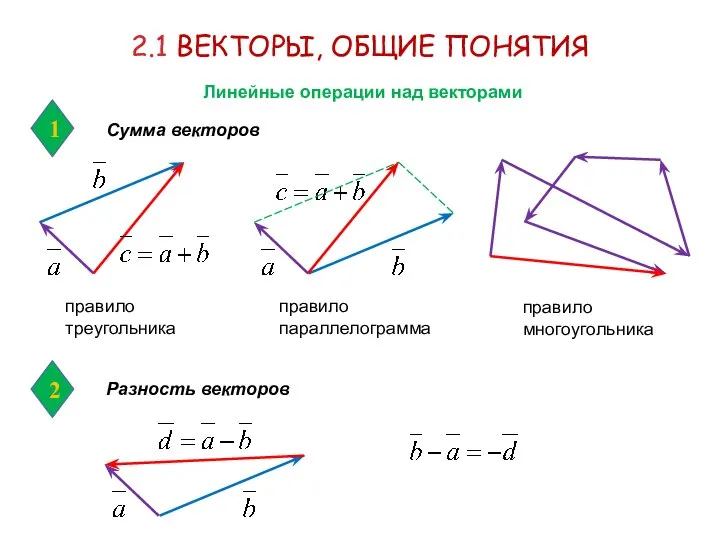
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Сумма векторов
Разность векторов
Линейные операции над векторами
1
правило треугольника
правило параллелограмма
правило многоугольника
2

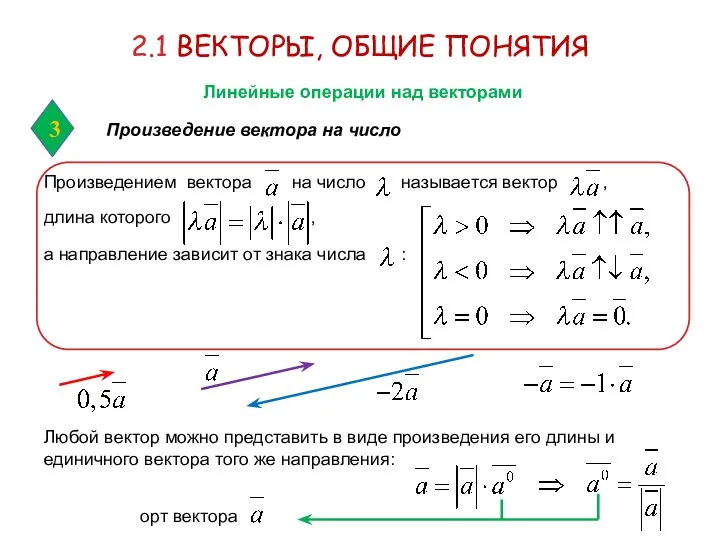
а направление зависит от знака числа :
Произведением вектора на число называется вектор ,
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Произведение вектора на число
Линейные операции над векторами
3
Любой вектор можно представить в виде произведения его длины и единичного вектора того же направления:
длина которого ,
орт вектора

Два ненулевых вектора и коллинеарны тогда и только тогда, когда они отличаются только числовым множителем:
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Теорема
Линейные операции над векторами
Свойства линейных операций над векторами.
1.
2.
3.
4.
5.
6.
7.
8.

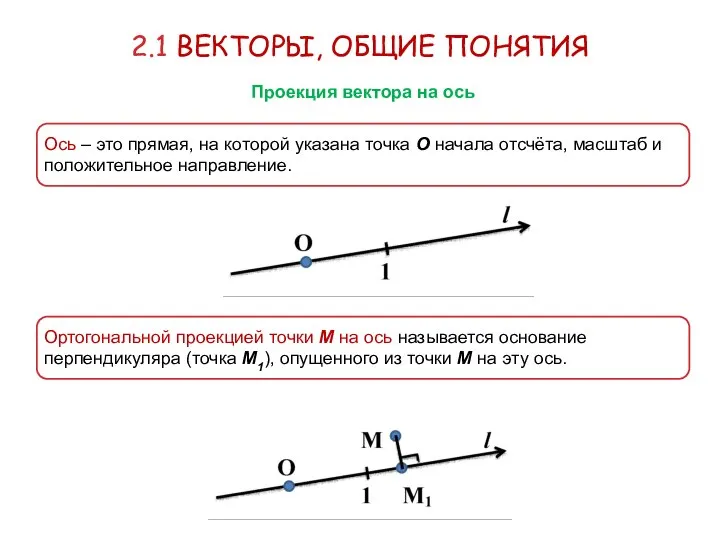
Ось – это прямая, на которой указана точка О начала отсчёта, масштаб и положительное направление.
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Проекция вектора на ось
Ортогональной проекцией точки М на ось называется основание перпендикуляра (точка М1), опущенного из точки М на эту ось.

«+» берётся, если «-» берётся, если
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Проекция вектора на ось
Проекцией вектора на ось называется число
Если точки А1 и В1 совпадают, то

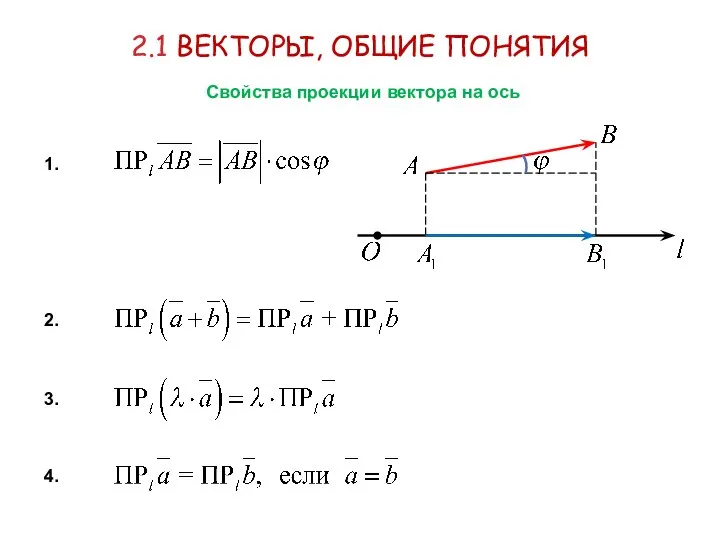
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Свойства проекции вектора на ось
1.
2.
3.
4.

Базисом на прямой (R1) называется любой ненулевой вектор, принадлежащий этой прямой.
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Базис
Базисом на плоскости (R2) называется любая упорядоченная пара неколлинеарных векторов, принадлежащих этой плоскости.
Базисом в пространстве (R3) называется любая упорядоченная тройка некомпланарных векторов.
Разложение вектора по базису на прямой:
Разложение вектора по базису на плоскости:
Разложение вектора по базису в пространстве:
Коэффициенты в разложении вектора по базису называются координатами вектора.

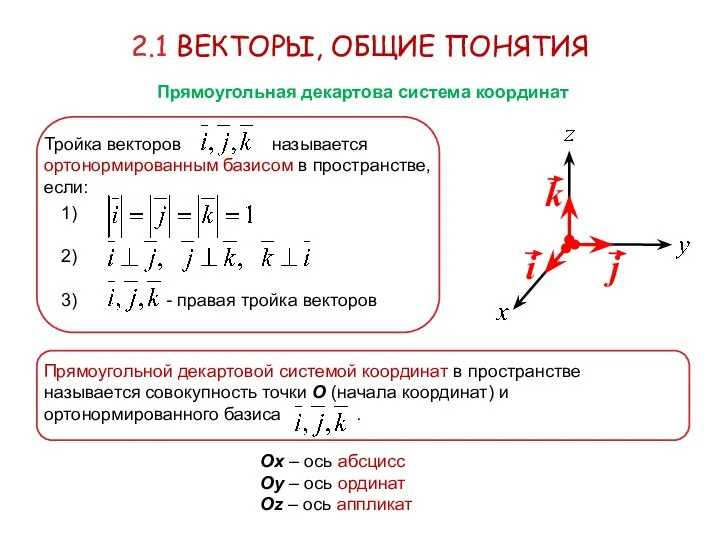
Тройка векторов называется ортонормированным базисом в пространстве, если:
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Прямоугольная декартова система координат
Прямоугольной декартовой системой координат в пространстве называется совокупность точки О (начала координат) и ортонормированного базиса .
1)
2)
3) - правая тройка векторов
Ox – ось абсцисс
Oy – ось ординат
Oz – ось аппликат

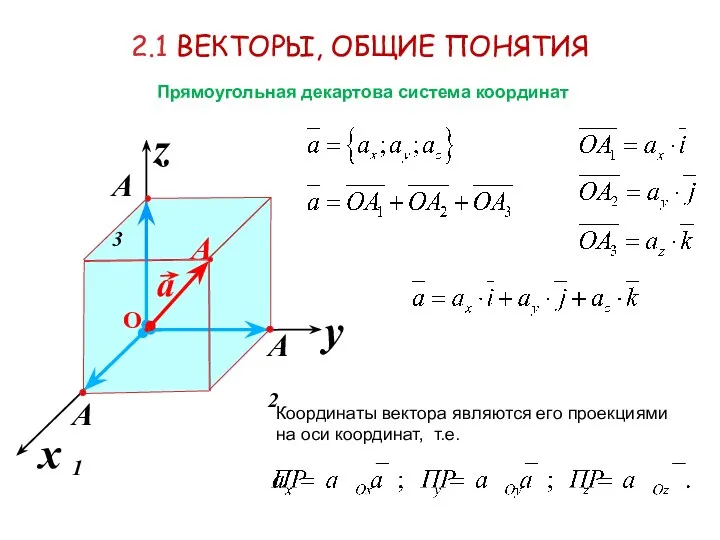
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Прямоугольная декартова система координат
Координаты вектора являются его проекциями на оси координат, т.е.

2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Длина и направление вектора
- длина вектора
- называются направляющими косинусами вектора в пространстве.
Направляющие косинусы какого-либо вектора являются координатами единичного вектора того-же направления:

Пример
Определить длину и направление вектора
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ

2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Сумма (разность) векторов
Умножение вектора на число
Линейные операции над векторами в координатах
1
При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются).
2
При умножении вектора на число, все его координаты умножаются на это число.
Сравнение векторов в координатах
Два вектора равны тогда и только тогда, когда равны их соответствующие координаты.
Коллинеарность векторов в координатах
Теорема.
Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны:
!

если
Примеры
1. Найти длину вектора
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
2. Проверить коллинеарность векторов если
верно!

2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Координаты вектора по координатам его начала и конца
Дано:
Найти: координаты вектора
Решение:
Расстояние между двумя точками

2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Координаты точки, которая делит отрезок в заданном соотношении
Дано:
Найти: координаты точки М.
Решение:

2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
Координаты середины отрезка
Дано:
Найти: координаты точки М.
Решение:

Примеры
1. Найти координаты точки М, которая делит отрезок АВ в соотношении 1/5, если
2.1 ВЕКТОРЫ, ОБЩИЕ ПОНЯТИЯ
2. Найти длину отрезка МВ.