Векторы в пространстве

Содержание
ПонятиеПонятие вектора
Равенство векторов
Сложение и вычитание векторов
Сумма нескольких векторов
Умножение вектора на число
Компланарные векторы
Правило параллелепипеда
Разложение вектора по трем некомпланарным векторам
Математический диктант
Контрольный тест

Понятие вектора
Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым.
ТТ – нулевой вектор ( ТТ = О)
А
В
С
D
T

Длина вектора
Длиной ненулевого вектора АВ называется длина отрезка АВ.
Длина вектора АВ(вектора a) обозначается так: АВ ( a ).
Длина нулевого вектора считается равной нулю: 0 =0
А
В

Два ненулевых вектора называются коллинеарными ,если они лежат на одной прямой или на параллельных прямых.
Два ненулевых вектора ОР и КМ коллинеарны и при этом лучи ОР и КМ соноправлены
Векторы ОР и КМ называются соноправленными
Если лучи не являются соноправленными, то векторы называются противоположно направленными.
Нулевой вектор считается соноправленным с любым вектором.
ОР КМ; CD КМ ; TL AB ; CD OP
А
В
С
D
К
М
F
L
T
O
P

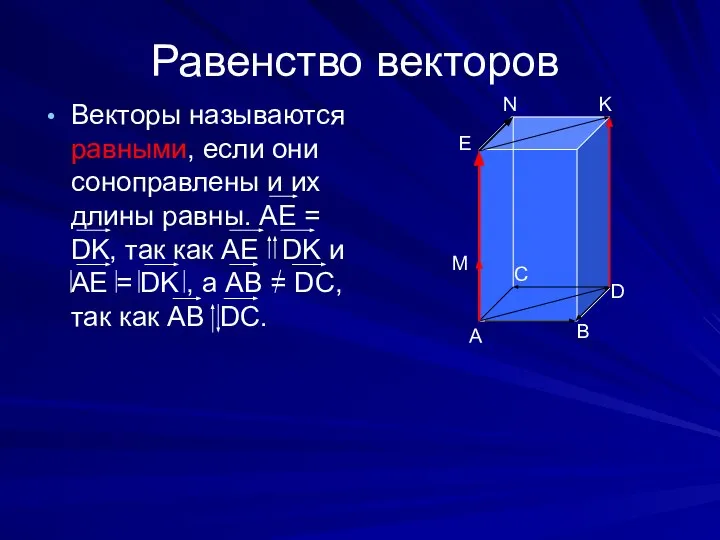
Равенство векторов
Векторы называются равными, если они соноправлены и их длины равны. АЕ = DK, так как АЕ DK и АЕ = DK , а АВ = DC, так как АВ DC.
A
B
D
N
K
E
C
M

От любой точки можно отложить вектор, равный данному, и притом только один.
Доказательство. В самом деле, пусть а – данный вектор, М – данная точка. Проведем через начало и конец вектора а и точку М плоскость и в этой плоскости построим вектор MN = a. Очевидно, что вектор MN искомый. Из построения ясно также, что MN – единственный вектор с началом М, равный вектору а.
а
М
N

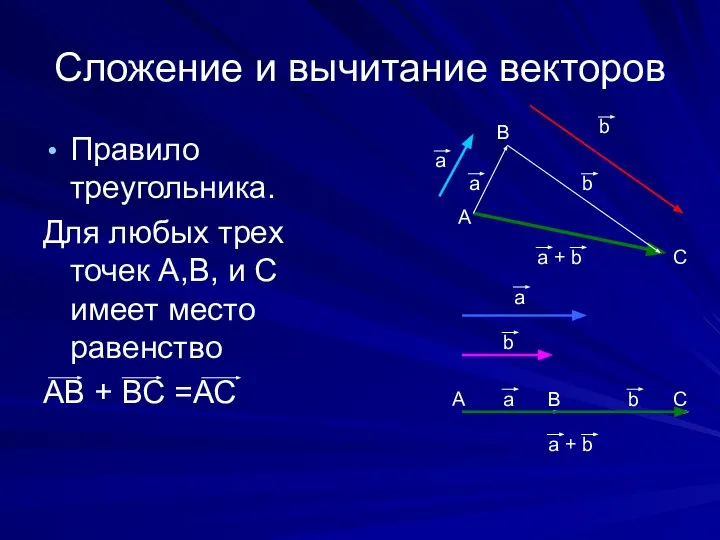
Сложение и вычитание векторов
Правило треугольника.
Для любых трех точек А,В, и С имеет место равенство
АВ + ВС =АС
А
С
В
а
а
b
b
a + b
а
b
A
C
B
a
b
a + b

Свойства сложения векторов.
Для любых векторов а, b, с справедливы равенства:
1) а + b = b + a ( переместительный закон)
2) ( а+b ) + c = a + ( b + c ) ( cочетательный закон )
Правило параллелограмма сложения двух неколлинеарных векторов
а
а + в
b
a
b

Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены. Вектором, противоположным нулевому вектору, считается нулевой вектор.
АВ и ВА - противоположные векторы
А
В

Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а.
Разность а - b векторов а и b можно найти по формуле а - b = a + (-b) , где
(-b) – вектор, противоположный вектору b.
а
b
- b
а - b
а
В
А
О
А
О
В
а
b
а - b

Сумма нескольких векторов
Сумма нескольких векторов не зависит от того, в каком порядке они складываются.
Правило многоугольника.
Если А1 , А2, …, Аn - произвольные точки, то А1А2 + А2А3+…+Аn-1Аn = А1Аn
OC = a + b + c
O
C
A
B
a
b
c

Умножение вектора на число
Произведением ненулевого вектора а на число к называется такой вектор b, длина которого равна к * а , причем векторы а и b сонаправлены при к > 0 и противоположно направлены при к < 0.
Если а = 0, то b = 0.
Если к = 0, то b = 0.
Основные свойства
(kl)a = k(la) сочетательный закон
k( a + b ) = ka + kb I распределительный закон
( k + l )a = ka + la II распределительный закон
Если а и b коллинеарны и а = о, то существует к, что b=ka.

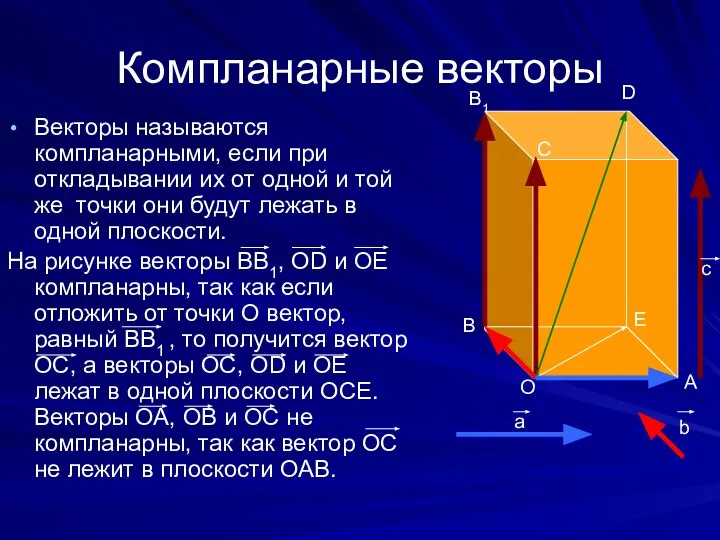
Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
На рисунке векторы ВВ1, ОD и ОЕ компланарны, так как если отложить от точки О вектор, равный ВВ1 , то получится вектор ОС, а векторы ОС, ОD и ОЕ лежат в одной плоскости ОСЕ. Векторы ОА, ОВ и ОС не компланарны, так как вектор ОС не лежит в плоскости ОАВ.
а
b
c
B1
D
C
B
O
A
E

Признак копланарности трех векторов
Если вектор с можно разложить по векторам а и b, т.е. представить в виде с = ха + уb, где х и у – некоторые числа, то векторы а, b и с компланарны.
Справедливо и обратное утверждение : если векторы а,
b и с компланарны, а векторы а и b не коллинеарны, то вектор с можно разложить по векторам а и b, причем коэффициенты разложения определяются единственным образом.
В1
А1
С
а
b
ОА1=х*ОА
ОВ1=у*ОВ
ОС= х*ОА + у*ОВ
В
А

Правило параллелепипеда
Пусть а, b, с – некомпланарные векторы. Отложим от произвольной точки О пространства векторы ОА=а, ОВ=b, ОC=с и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были его ребрами. Тогда диагональ ОD этого параллелепипеда изображает сумму векторов а, b и с : ОD = а + b + с. Действительно, ОD = ОЕ + ЕD = (ОА + АЕ) + ЕD= ОА + ОВ + ОC = а + b + c
а
b
B1
C
B
O
E
D
c
A

Разложение по трем некомпланарным векторам
Если вектор р представлен в виде
р = ха + уb + zc, где x, y и z – некоторые числа, то говорят, что вектор р разложен по векторам а, b и с. Числа х, у, z называются коэффициентами разложения.
Теорема.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
С
с
О
Р
р
В
Р2
а
А
b
P1

Математический диктант
Нарисуйте параллелепипед АВСDA1В1С1D1.
Найдите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а)АВ + A1D1 + СA1; б) СA1 + АD + D1 С1.
Найдите вектор, равный: а) АD - С1D1 - ВВ1 ; б) АВ - АA1 - С1В1
Представьте вектор ВС1 в виде разности двух векторов, один из которых вектор ВD1; вектор D1В.
Упростите выражение: а) MN – PQ – NM + RQ + TR; б) LP + MS + EN – MN – PL + ST
Упростите выражение: а) 3( a + b ) – 4( 2a – b ) + a; б) m + 3( 2m – n) – 2( m – 4n)