Содержание
- 2. Понятие вектора Отрезок, для которого указано, какая его граничная точка является началом, а какая - концом,
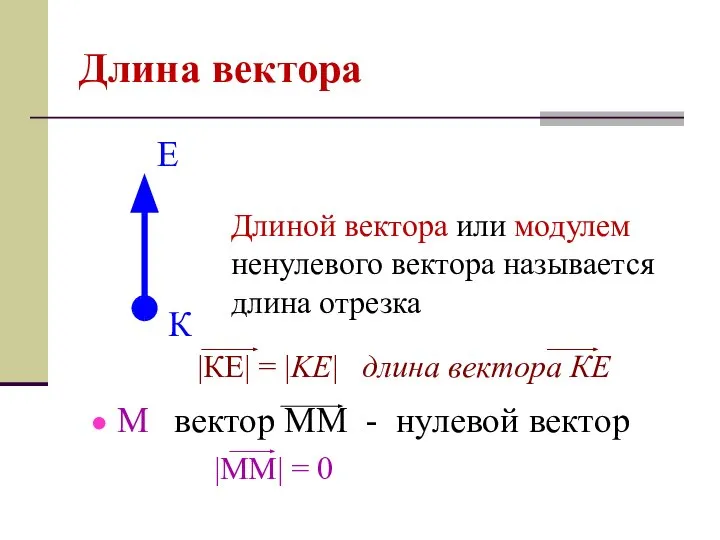
- 3. Длина вектора Длиной вектора или модулем ненулевого вектора называется длина отрезка
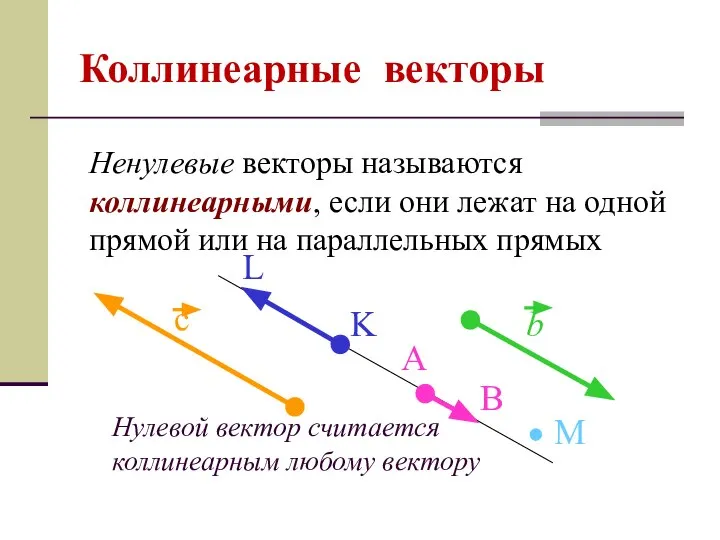
- 4. Нулевой вектор считается коллинеарным любому вектору Коллинеарные векторы Ненулевые векторы называются коллинеарными, если они лежат на
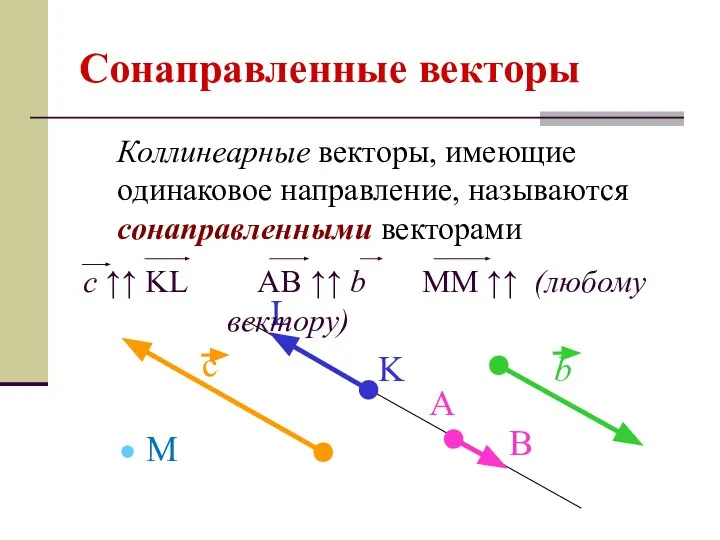
- 5. Сонаправленные векторы Коллинеарные векторы, имеющие одинаковое направление, называются сонаправленными векторами
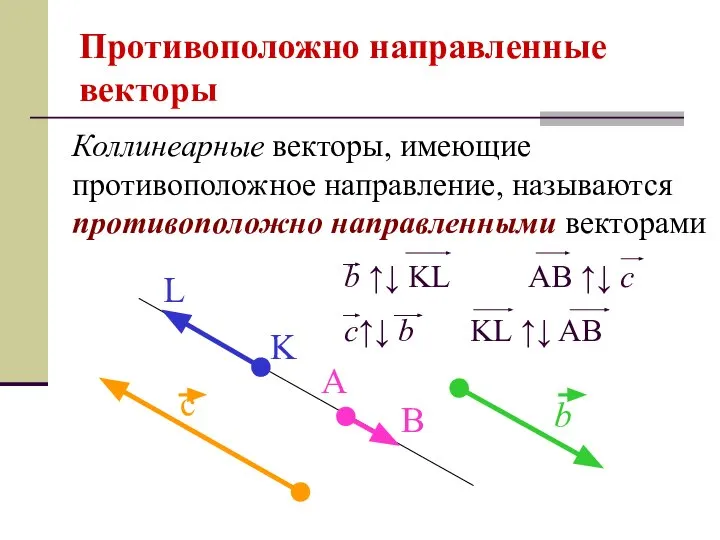
- 6. Противоположно направленные векторы Коллинеарные векторы, имеющие противоположное направление, называются противоположно направленными векторами
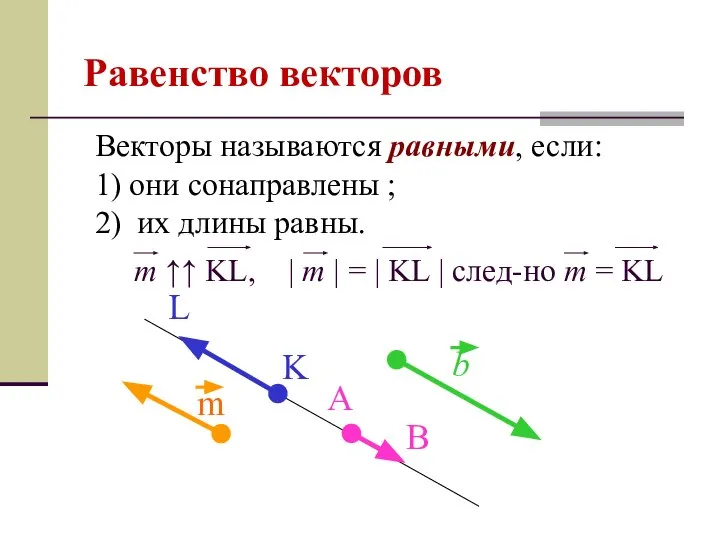
- 7. Равенство векторов Векторы называются равными, если: 1) они сонаправлены ; 2) их длины равны. m
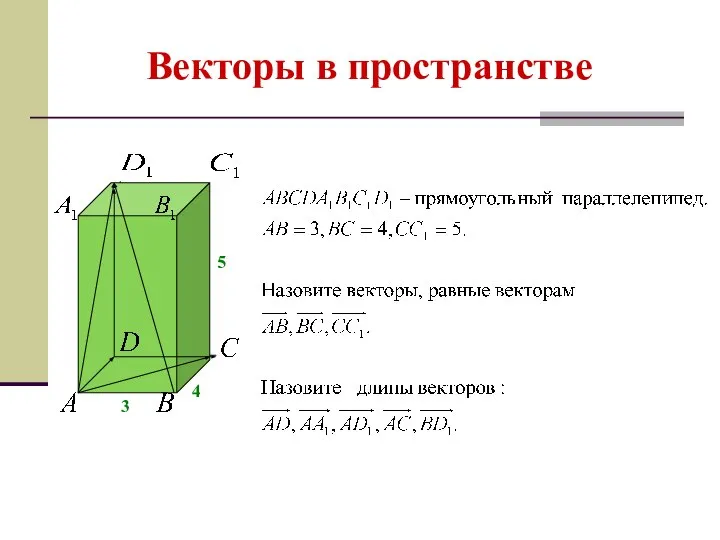
- 8. Векторы в пространстве
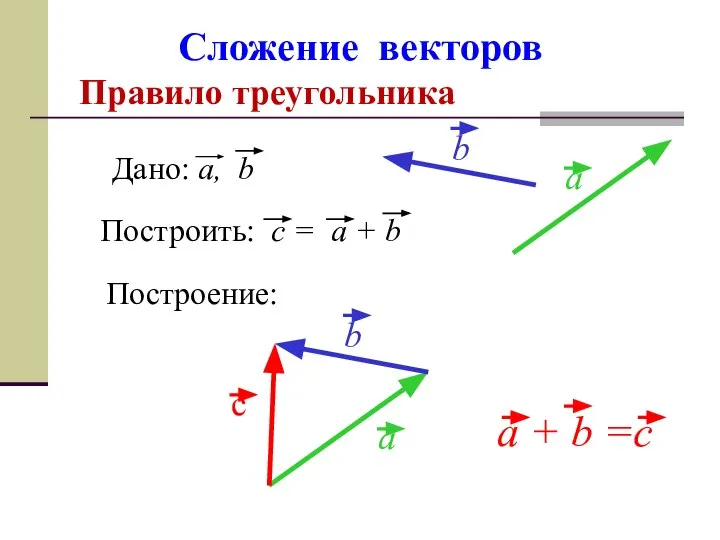
- 9. Сложение векторов Правило треугольника Построение:
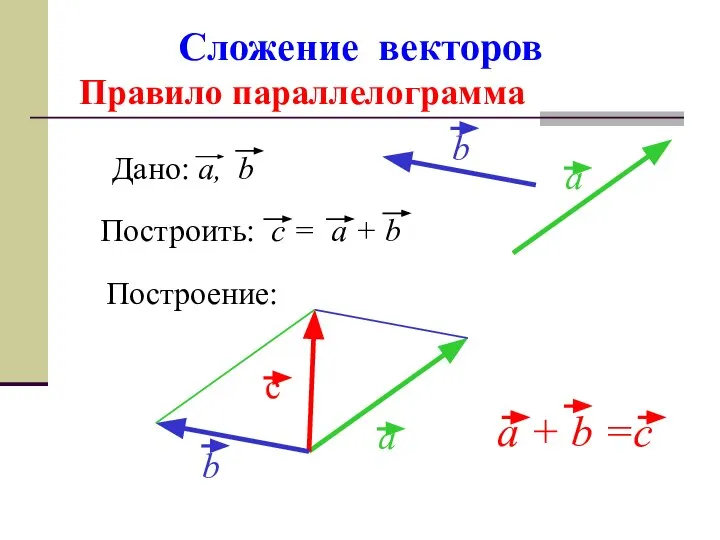
- 10. Сложение векторов Правило параллелограмма Построение:
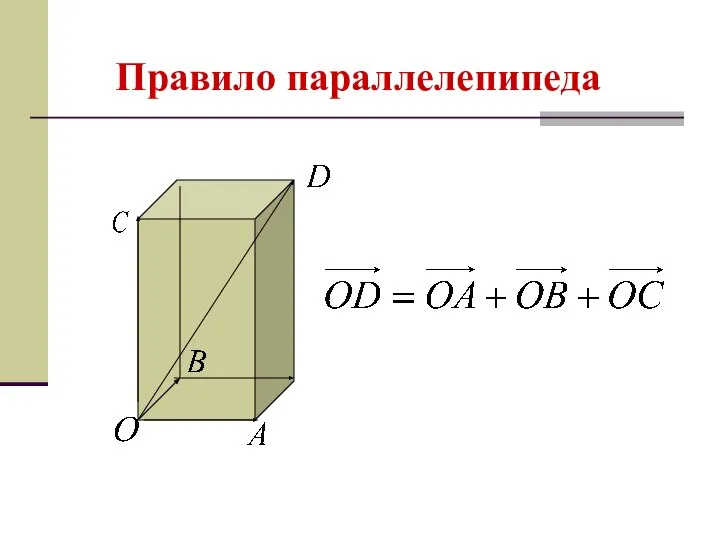
- 11. Правило параллелепипеда
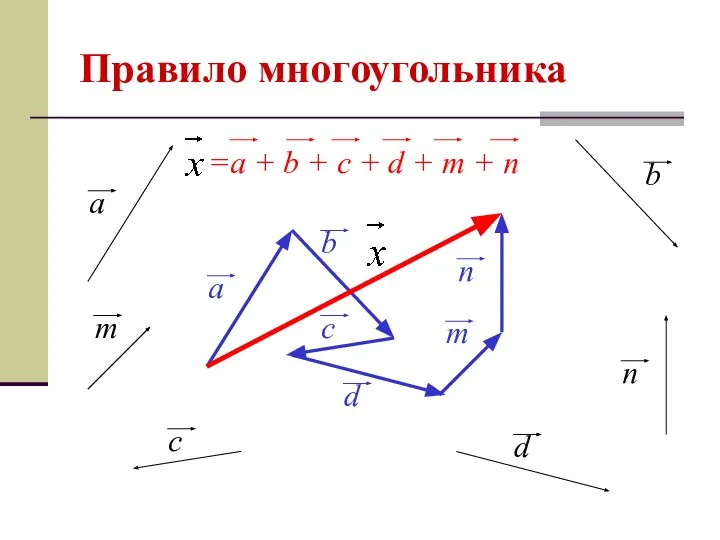
- 12. Правило многоугольника
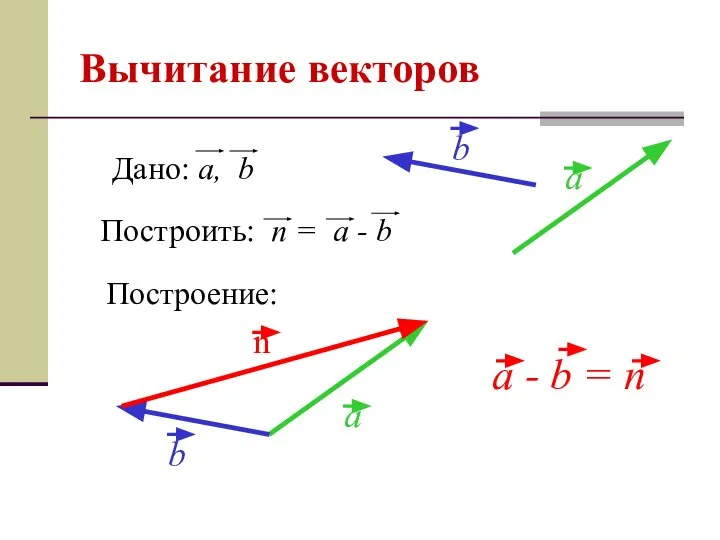
- 13. Вычитание векторов Построение:
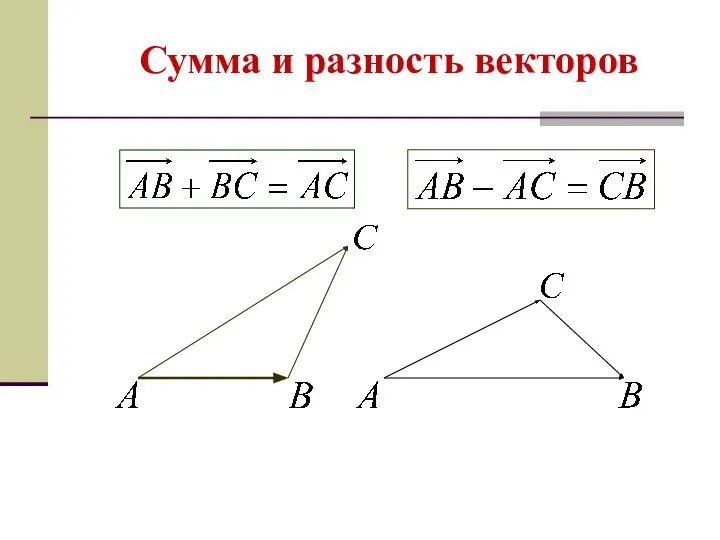
- 14. Сумма и разность векторов
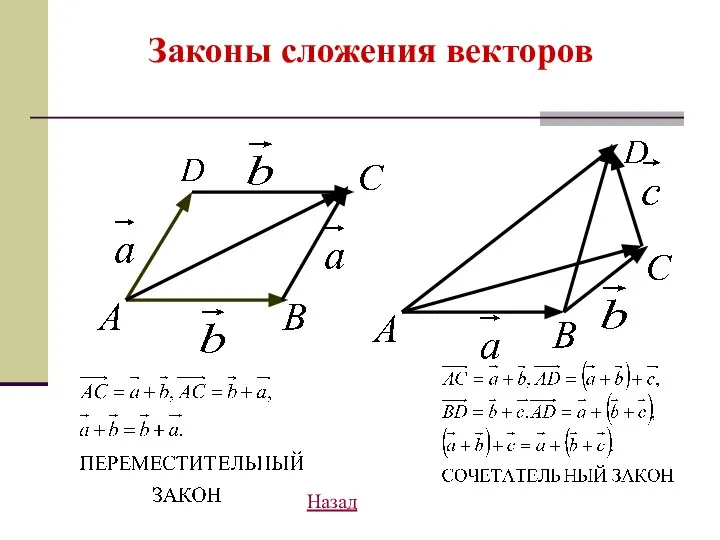
- 15. Законы сложения векторов Назад
- 16. Умножение вектора a на число k k·a = b, |a| ≠ 0, k – произвольное число
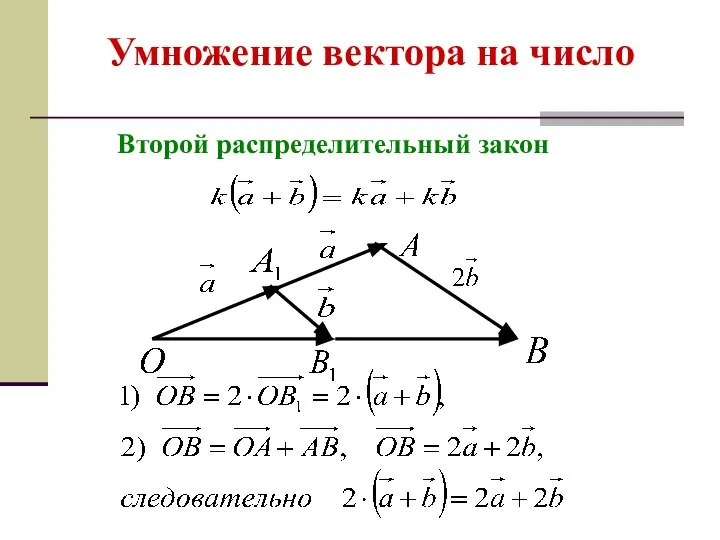
- 17. Умножение вектора на число
- 18. Умножение вектора на число
- 19. Умножение вектора на число
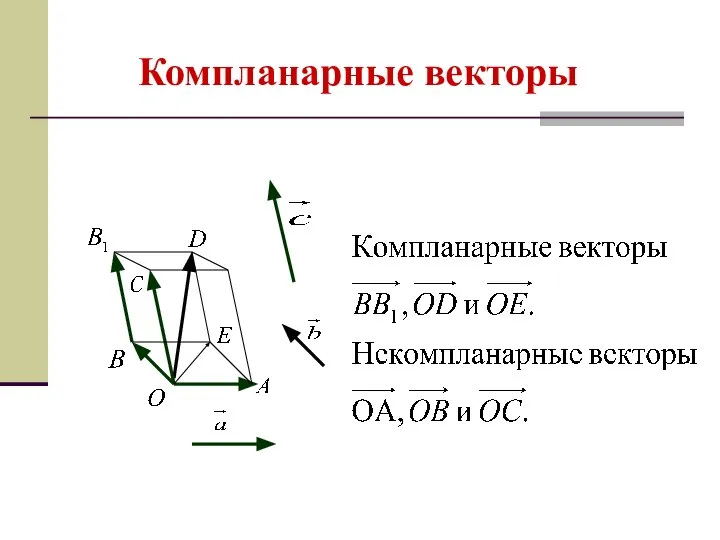
- 20. Компланарные векторы Векторы называются компланарными, если при откладывании их от одной точки они будут лежать в
- 21. Компланарные векторы
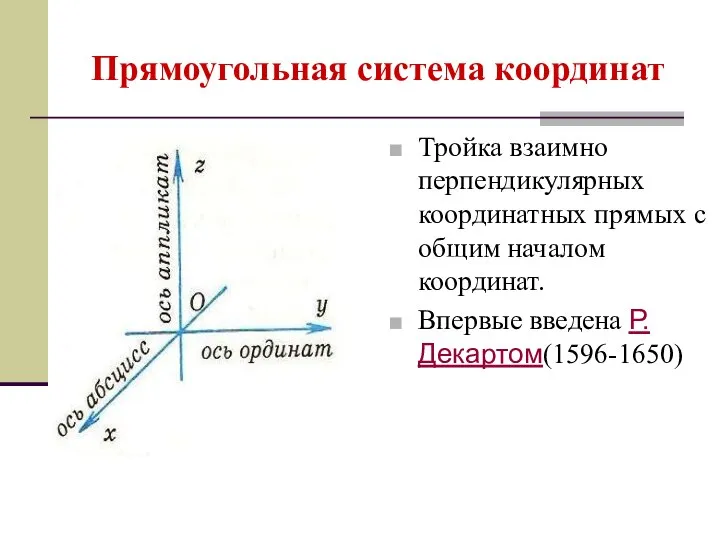
- 22. Прямоугольная система координат Тройка взаимно перпендикулярных координатных прямых с общим началом координат. Впервые введена Р.Декартом(1596-1650)
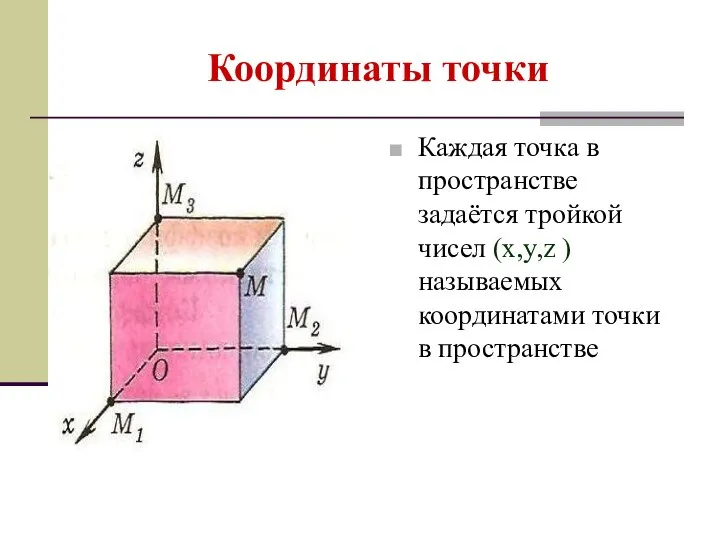
- 23. Координаты точки Каждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых координатами точки в пространстве
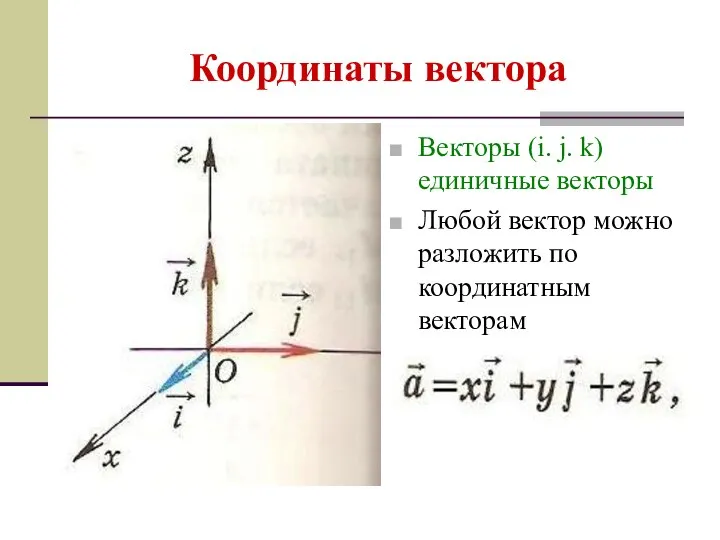
- 24. Координаты вектора Векторы (i. j. k) единичные векторы Любой вектор можно разложить по координатным векторам
- 25. Длина вектора
- 26. Скалярное произведение векторов
- 28. Скачать презентацию







 Презентация на тему УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ  Назначение формулы
Назначение формулы Тригонометрические уравнения. Арксинус
Тригонометрические уравнения. Арксинус Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Геометрические фигуры. 2 класс
Геометрические фигуры. 2 класс АВТОР: Краснова И.Я.
АВТОР: Краснова И.Я. Основы теории измерений
Основы теории измерений Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни
Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни Модуль числа
Модуль числа Байесовский анализ и сети Байеса
Байесовский анализ и сети Байеса Параллельные прямые в пространстве
Параллельные прямые в пространстве Постановка задач исследования операций, основы математического программирования и методов оптимизации
Постановка задач исследования операций, основы математического программирования и методов оптимизации Кривые второго порядка
Кривые второго порядка Величины
Величины Равенство векторов
Равенство векторов Признаки подобия треугольников
Признаки подобия треугольников Сечение поверхности плоскостью
Сечение поверхности плоскостью Решение систем неравенств
Решение систем неравенств Деление дробей. Путешествие в Китай
Деление дробей. Путешествие в Китай Линейные дискретные системы с постоянными параметрами. Лекция 6
Линейные дискретные системы с постоянными параметрами. Лекция 6 Задача сетевого планирования с вложением средств
Задача сетевого планирования с вложением средств Деление дробных чисел
Деление дробных чисел Приемы вычислений для случаев вида 26+7. 2 класс
Приемы вычислений для случаев вида 26+7. 2 класс Общие методы решения уравнений
Общие методы решения уравнений Принцип математической индукции (аксиома алгебры)
Принцип математической индукции (аксиома алгебры) Презентация на тему Прототипы В12. Задачи на проценты
Презентация на тему Прототипы В12. Задачи на проценты  Многогранники
Многогранники Операционный метод решения линейных дифференциальных уравнений и систем
Операционный метод решения линейных дифференциальных уравнений и систем