Содержание
- 2. Задача сетевого планирования с вложением средств
- 3. Задача сетевого планирования с вложением средств
- 4. Задача сетевого планирования с вложением средств
- 5. Тогда задача принимает следующий вид. Получаем задачу линейного программирования. Рассмотрим пример решения такой задачи симплекс-методом. Задача
- 6. Пример (вариант 50) Пусть имеется комплекс работ А1, А2, …, А7. Работы А3 и А4 опираются
- 7. Пример (вариант 50) Второе условие выполнено. Следовательно, критический путь не меняется. Преобразуем ограничение на критическое время.
- 8. Пример (вариант 50) Запишем данные в симплекс-таблицу. Получаем следующую задачу линейного программирования.
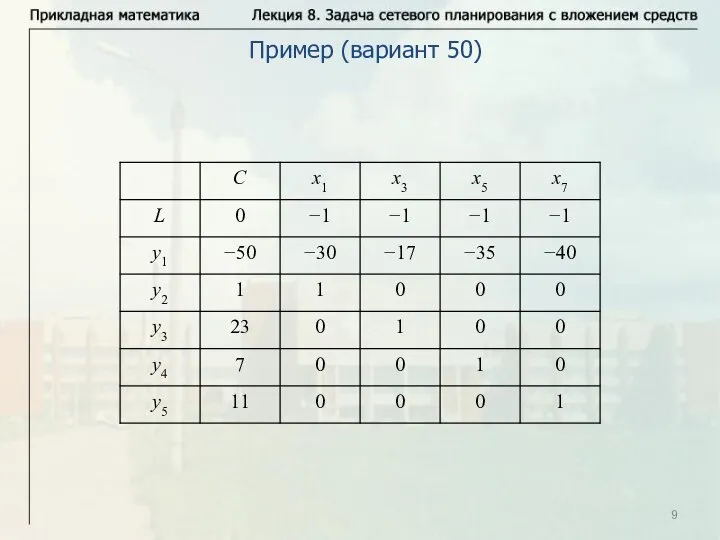
- 9. Пример (вариант 50)
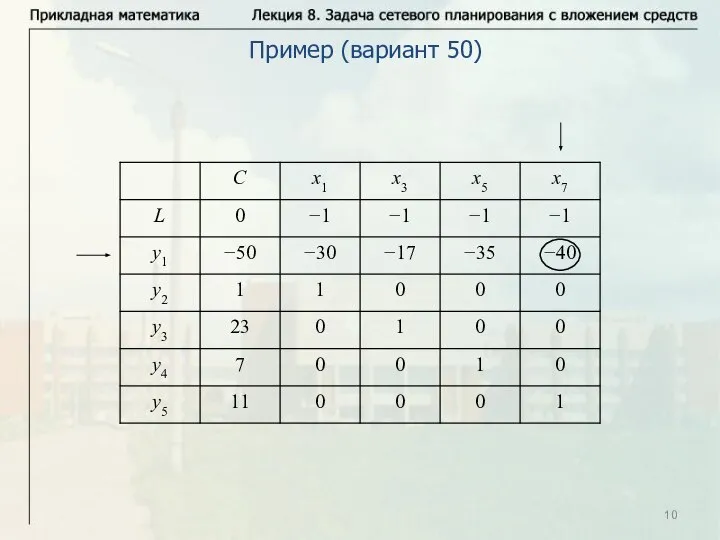
- 10. Пример (вариант 50)
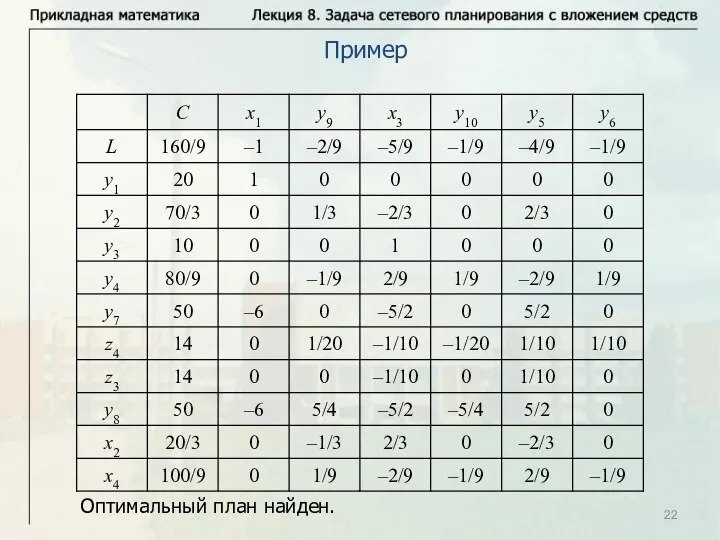
- 11. Пример (вариант 50) Оптимальный план найден.
- 12. Имеется комплекс работ А1, …, Аn. Будем считать, что время выполнения работ зависит от вложенных в
- 13. Пример Пусть имеется комплекс из четырех работ А1, А2, А3, А4. Работа А3 опирается на А1
- 14. Пример Преобразуем ограничения на связи между работами.
- 15. Пример Ограничения на связи между работами имеют вид Ограничения на завершения последних работ имеют вид После
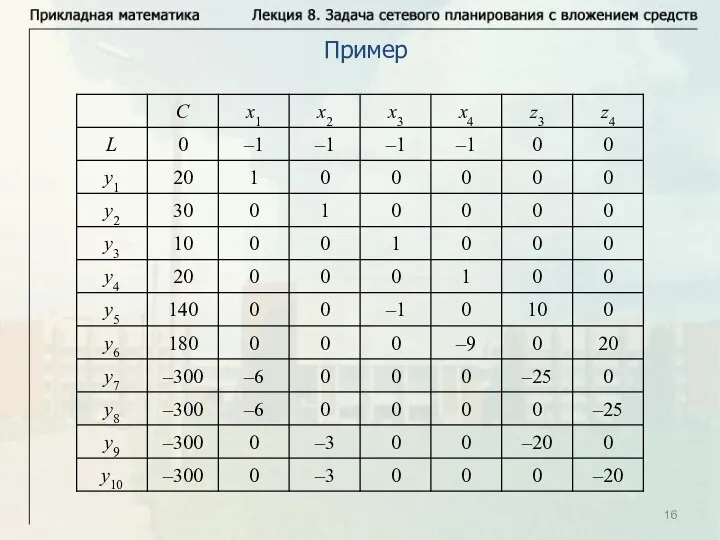
- 16. Пример
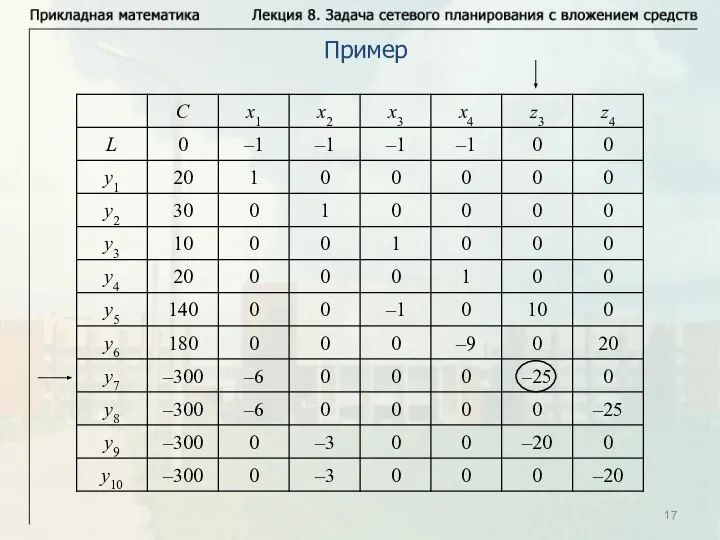
- 17. Пример
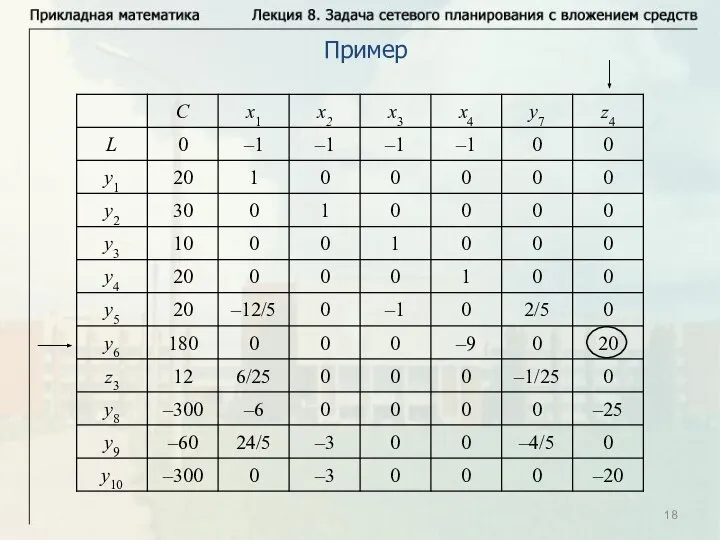
- 18. Пример
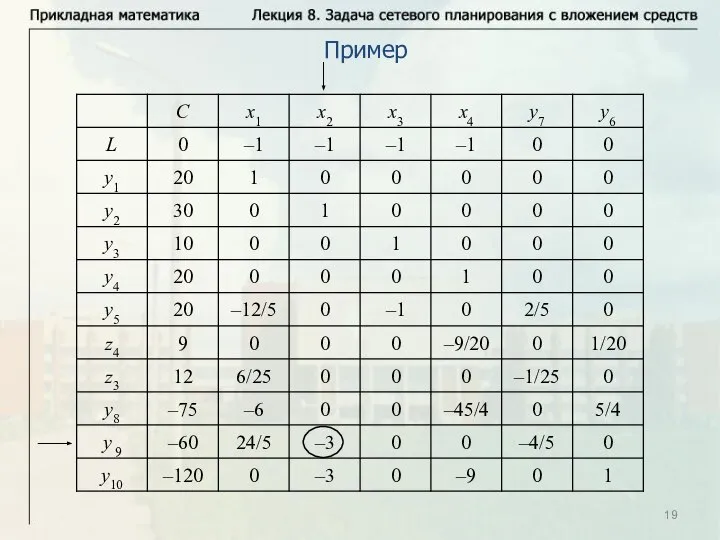
- 19. Пример
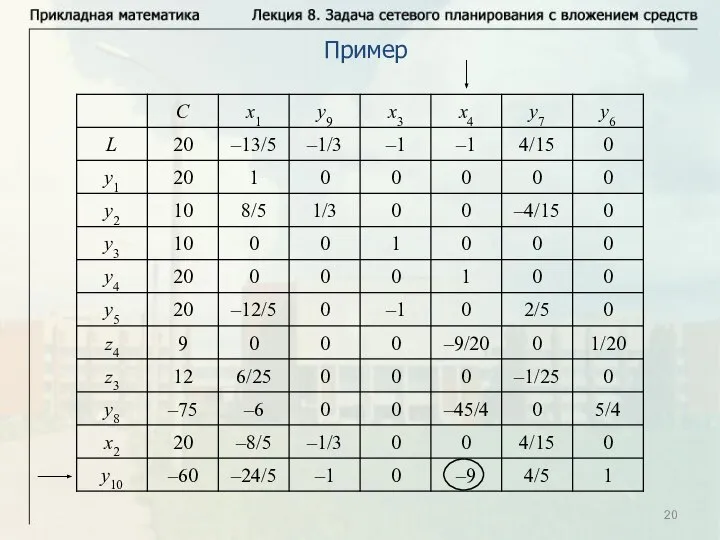
- 20. Пример
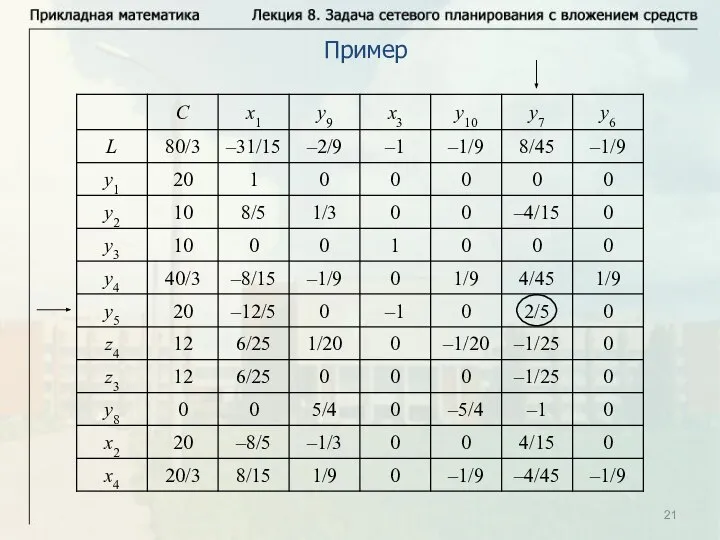
- 21. Пример
- 22. Пример Оптимальный план найден.
- 23. Пример Ответ: Проверка.
- 24. Пусть имеется комплекс работ А1, А2, …, А7. Работы А3 и А4 опираются на А1 и
- 26. Скачать презентацию














 Сечение куба и сечение тетраэдра
Сечение куба и сечение тетраэдра Образовательный минимум
Образовательный минимум Разложение многочлена на множители. Работа над ошибками
Разложение многочлена на множители. Работа над ошибками Путешествуем по странам Европы. 3 класс
Путешествуем по странам Европы. 3 класс Формулы нахождения объёма параллелеппипеда, объёма куба
Формулы нахождения объёма параллелеппипеда, объёма куба Теория вероятности. События и испытания
Теория вероятности. События и испытания Случаи вычитания 11-
Случаи вычитания 11- Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Презентация на тему Владимир Модестович Брадис
Презентация на тему Владимир Модестович Брадис  Окружность. Основные теоремы
Окружность. Основные теоремы Мультипликативная система индексов
Мультипликативная система индексов Решение текстовых задач арифметическим способом
Решение текстовых задач арифметическим способом Случаи вычитания 12-
Случаи вычитания 12- Площа прямокутника
Площа прямокутника Первообразная
Первообразная Сравнение обыкновенной дроби и десятичной
Сравнение обыкновенной дроби и десятичной Линейные измерения
Линейные измерения Сложение и вычитание рациональных чисел
Сложение и вычитание рациональных чисел Деление одночлена на одночлен
Деление одночлена на одночлен Решение уравнений с помощью систем
Решение уравнений с помощью систем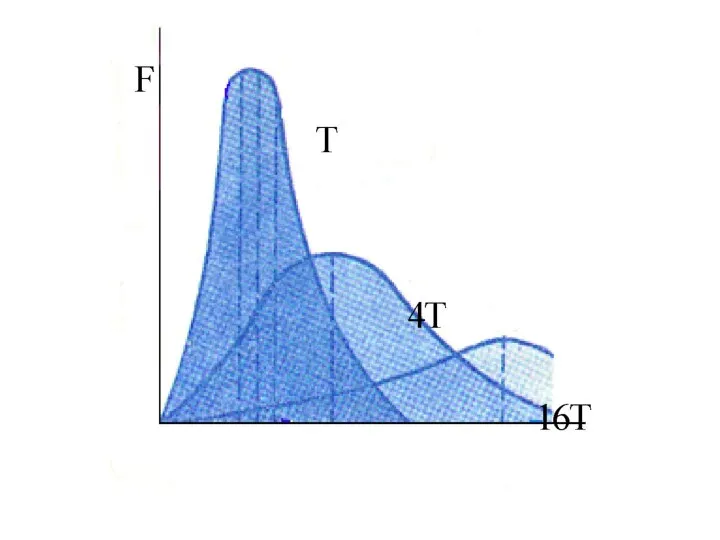 Функция распределения Максвелла
Функция распределения Максвелла Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Одночлен и его стандартный вид
Одночлен и его стандартный вид Презентация на тему Площадь круга
Презентация на тему Площадь круга  Пять великих математиков
Пять великих математиков Медианы, биссектрисы и высоты треугольника. 7 класс
Медианы, биссектрисы и высоты треугольника. 7 класс Решение задач на параллельность прямых и плоскостей
Решение задач на параллельность прямых и плоскостей