Содержание
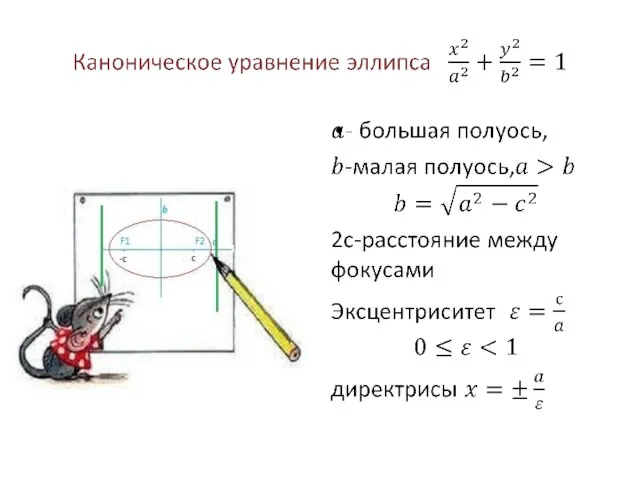
- 2. Уравнение эллипса.
- 6. Примеры
- 7. А как мы запишем уравнение вот такого эллипса и его характеристики?
- 8. Уравнение эллипса в центром-НЕ в начале координат. Выделение полного квадрата.
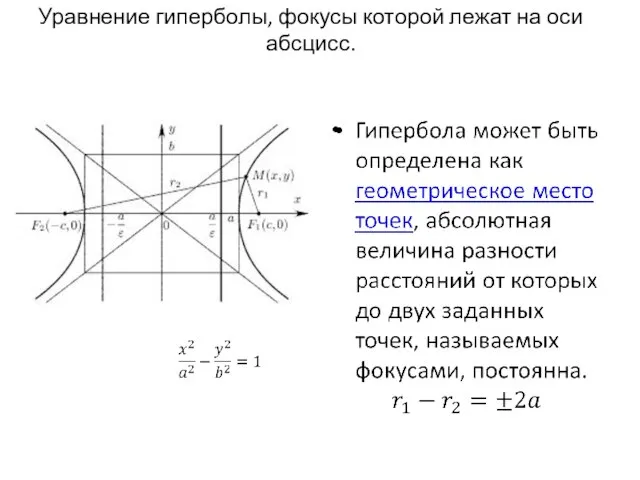
- 9. Уравнение гиперболы, фокусы которой лежат на оси абсцисс.
- 10. Другие варианты канонического уравнения гиперболы. Самостоятельно: Записать связь между a , b и c для гипербол
- 11. Каноническое уравнение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом
- 13. Скачать презентацию








 Тест по математике: меры времени (выражение в крупных мерах)
Тест по математике: меры времени (выражение в крупных мерах) Устный счёт. Назови числа по порядку
Устный счёт. Назови числа по порядку Параллельные прямые
Параллельные прямые Разложение многочленов на множители с помощью комбинации различных приёмов
Разложение многочленов на множители с помощью комбинации различных приёмов Комплексный анализ. Аналитические функции и конформные отображения
Комплексный анализ. Аналитические функции и конформные отображения Упрощение логических выражений
Упрощение логических выражений Задачи на уменьшение числа в несколько раз
Задачи на уменьшение числа в несколько раз Отношения и пропорции. Игра Кот в мешке
Отношения и пропорции. Игра Кот в мешке Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел Теорема невесты
Теорема невесты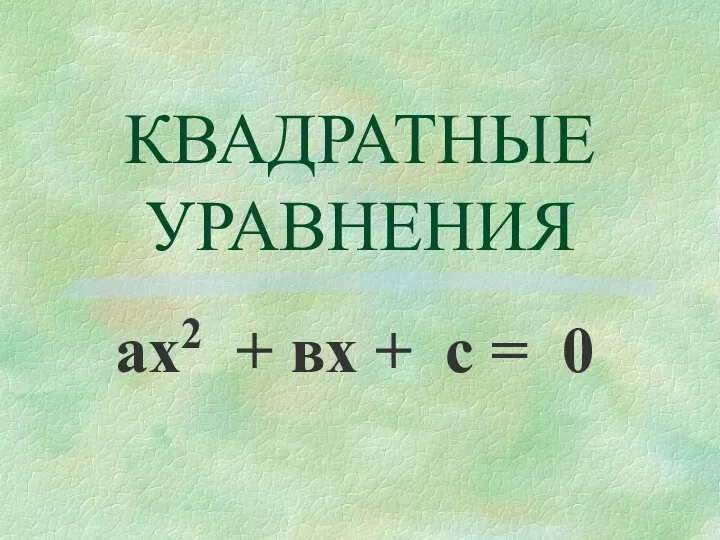 Квадратные уравнения ах2 + вх + с = 0
Квадратные уравнения ах2 + вх + с = 0 Применение технологий Веб 2.0 на уроках математики
Применение технологий Веб 2.0 на уроках математики Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками
Вычисление координат середины отрезка. Вычисление длины отрезка по его координатам. Вычисление расстояния между двумя точками Геометрический смысл производной
Геометрический смысл производной Анимированный плакат Цифры – прописи
Анимированный плакат Цифры – прописи Квадратичная функция и её график. Методические материалы урока
Квадратичная функция и её график. Методические материалы урока Игра-тренажёр Орехи для белочки
Игра-тренажёр Орехи для белочки Однородные системы линейных алгебраических уравнений
Однородные системы линейных алгебраических уравнений Модель плоскости
Модель плоскости Понятие логарифма
Понятие логарифма Знакомство с линиями чертежа
Знакомство с линиями чертежа Решение задач. Подготовка к контрольной работе
Решение задач. Подготовка к контрольной работе Прямоугольный параллелепипед
Прямоугольный параллелепипед Презентация на тему Квадратное уравнение и его корни
Презентация на тему Квадратное уравнение и его корни  первые уроки геометрии
первые уроки геометрии Деление с остатком
Деление с остатком Презентация на тему Математика ЕГЭ 2012
Презентация на тему Математика ЕГЭ 2012  be798f8c4ede43fcabd1090e739d523d
be798f8c4ede43fcabd1090e739d523d