Тригонометрические уравнения. Арксинус

Рассмотрим sin(x)= √3/2.
Для решения нашего уравнения требуется построить прямую y= √3/2 и посмотреть в каких точках она пересекает числовую окружность.
Видно что прямая пересекает окружность в двух точках F и G, эти точки и будут решениями уравнения, переобозначим F как x1, а G как x2. Решение нашего уравнения мы находили и получили
x1 = π/3 + 2πk, а x2= 2π/3+2πk.
Решить данное уравнение довольно таки просто, но как решить например уравнение sin(x)=5/6. Очевидно что это уравнение будет иметь так же два корня, но какие значения будут соответствовать решению на числовой окружности?
Что такое арксинус?

Давайте внимательно посмотрим на наше уравнение sin(x)=5/6
Обозначение арксинуса
Решениями нашего уравнения будут две точки F= x1+2πk и G=x2+2πk.
x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π-x1, т.к. AF=AC-FC, но FC=AG, AF=AC-AG= π-x1
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается как арксинус.
Тогда решения нашего уравнения запишутся как:
x1=arcsin (5/6)
x2= π -arcsin (5/6)
Тогда решение в общем виде:
X = arcsin (5/6) +2πk и x = π - arcsin (5/6) +2πk
Арксинус это угол(длина дуги AF, AG) синус которого равен 5/6

Немного истории.
История происхождения нашего символа совершенно такая же как и у arccos:
Символ arcsin появляется впервые в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа, несколько ранее понятие арксинус уже рассматривал Д. Бернули, правда записывал другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга), что вполне согласуется со смыслом понятия: arcsin x, например, - это угол (а можно сказать и дуга), синус которого равен x.
Жозе́ф Луи́ Лагра́нж

Определение.
Определение. Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x) = a имеет решение:
x= arcsin(a) + 2πk и x= π -arcsin(a) + 2πk
Перепишем:
x= π -arcsin(a) + 2πk= -arcsin(a) + π(1+2k)
Ребята, посмотрите внимательно на два наших решения, как думаете можно ли их записать общей формулой?
Заметим, если перед арксинусом стоит знак “плюс”, то π умножается на четное число 2πk, а если знак “минус”, то множитель нечетный 2k+1. Тогда запишем общую формула решения для уравнения sin(x)=a

Определение.
Есть три случая в которых предпочитают записывать более простым способом решения:
sin(x)=0, то x= πk
sin(x)=1, то x= π/2 + 2πk
sin(x)=-1, то x= -π/2 + 2πk
Для любого -1 ≤ а ≤ 1 выполняется равенство
arcsin (-a)= - arcsin (a)

Таблица значений арксинуса.
Таблица значений арксинуса:
Таблица значений синуса:

Пример
Вычислить а) arcsin(√3/2) б) arcsin(-1/2) в) arcsin(0)
a) Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2 и по определению - π/2≤ x≤ π/2,
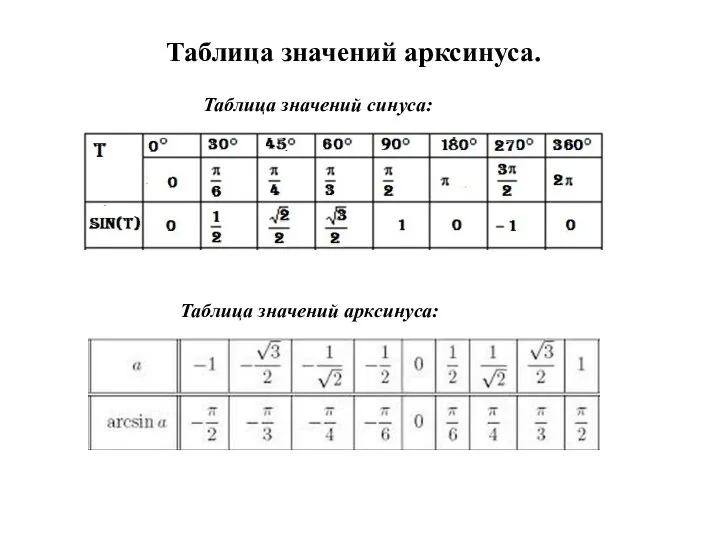
посмотрим значения синуса в таблице:
x=π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2
Ответ: arcsin(√3/2)=π/3
б) Пусть arcsin(-1/2) = x, тогда sin (x)= -1/2 и по определению - π/2≤ x≤ π/2,
посмотрим значения синуса в таблице:
x=-π/6, т.к. sin(-π/6)= -1/2 и - π/2≤ -π/6≤ π/2
Ответ: arcsin(-1/2)=-π/6
в) Пусть arcsin(0) = x, тогда sin(x)= 0и по определению - π/2≤ x≤ π/2,
посмотрим значения синуса в таблице:
значит x=0, т.к. sin(0)= 0 и - π/2≤ 0 ≤ π/2
Ответ: arcsin(0)=0
Решение: