Содержание
- 2. Что нужно знать? Задачи на проценты. 1. Выражение показывает, сколько процентов число а составляет от числа
- 3. Составь выражение. Чашка стоит х рублей, блюдце на у % дешевле. На сколько процентов чашка дороже
- 4. Составь выражение. Чашка стоит х рублей, блюдце на у % дешевле. На сколько процентов блюдце дешевле
- 5. Составь выражение. Чашка стоит х рублей, блюдце на у % дешевле. Сколько процентов чашка составляет от
- 6. Практические советы. Задачи на проценты. 1. Очень тщательно изучи, от чего нужно считать проценты. Если об
- 7. (№ 99565) В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате
- 8. Вт: подешевели на 0,01y(х+0,01ух) руб. и стали стоить (х+0,01ух)-0,01у(х+0,01ух)= (х-0,0001у2х) руб. Пусть х руб. стоили акции
- 9. (№ 99567) Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки? Ответ:
- 10. (№ 99568) Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась
- 11. (№ 99568) Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась
- 12. (№ 99570) Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес
- 13. (№ 99574) Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения
- 14. Задачи на смеси и сплавы.
- 15. Что нужно знать? Задачи на проценты (смеси и сплавы).
- 16. (№ 99571) В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды.
- 17. (№ 99572) Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого
- 18. (№ 108697) Смешали 3 литра 25-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора
- 19. (№ 109111) Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих
- 20. (№ 109159) Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы
- 21. (№ 109211) Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный
- 22. (№ 109211) Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный
- 24. Скачать презентацию





















 Теплицы
Теплицы Построение графика функции, используя её свойства
Построение графика функции, используя её свойства Математические методы в психологии. Генеральная совокупность и выборка
Математические методы в психологии. Генеральная совокупность и выборка Декартова система координат в пространстве
Декартова система координат в пространстве Построение кривой времени t=f(s) методом инженера Лебедева
Построение кривой времени t=f(s) методом инженера Лебедева Числото шест
Числото шест Законы умножения для обыкновенных дробей. 5 класс
Законы умножения для обыкновенных дробей. 5 класс Задачи на части
Задачи на части Оснащение математических уголков в ДОУ
Оснащение математических уголков в ДОУ Ряды распределения. Практическое занятие 4
Ряды распределения. Практическое занятие 4 Тема: виды линий. Какие бывают линии?
Тема: виды линий. Какие бывают линии? Статистические графики
Статистические графики Степенная функция и её график
Степенная функция и её график Возможности символьного вычисления в среде MatLab
Возможности символьного вычисления в среде MatLab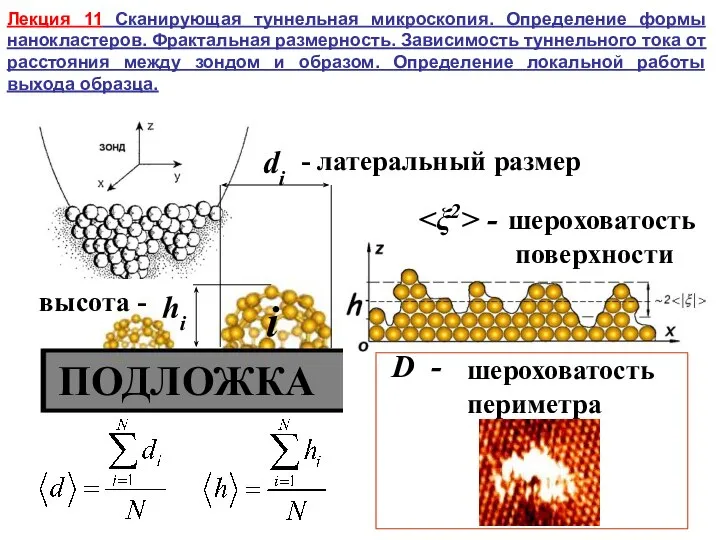 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Статистическая теория радиотехнических систем. Согласованный линейный фильтр. (Лекция 12)
Статистическая теория радиотехнических систем. Согласованный линейный фильтр. (Лекция 12) Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ Виды и особенности нелинейных систем
Виды и особенности нелинейных систем Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Функция y = cos x. Ее свойства и график
Функция y = cos x. Ее свойства и график Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Решение задач по теме Параллелограмм в рисунках
Решение задач по теме Параллелограмм в рисунках Применение математики в экономических исследованиях
Применение математики в экономических исследованиях Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Применение теоремы Пифагора при решении задач
Применение теоремы Пифагора при решении задач Параллельность прямых. Урок – практикум
Параллельность прямых. Урок – практикум триг.преоб-ПНК
триг.преоб-ПНК Возведение в степень. Диктант
Возведение в степень. Диктант