Вклад Гаусса в развитии теории комплексных чисел

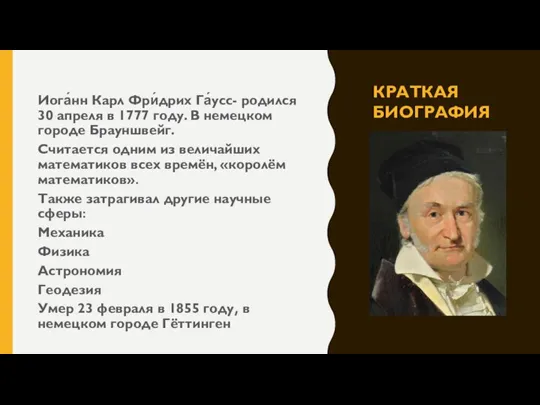
КРАТКАЯ
БИОГРАФИЯ
Иога́нн Карл Фри́дрих Га́усс- родился 30 апреля в 1777 году. В немецком городе Брауншвейг.
Считается одним из величайших математиков всех времён, «королём математиков».
Также затрагивал другие научные сферы:
Механика
Физика
Астрономия
Геодезия
Умер 23 февраля в 1855 году, в немецком городе Гёттинген

ДОСТИЖЕНИЯ ГАУСCА
В ОБЛАСТИ АЛГЕБРЫ
Гаусс дал первые строгие, даже по современным критериям, доказательства основной теоремы алгебры.
Он открыл кольцо целых комплексных гауссовых чисел, создал для них теорию делимости и с их помощью решил немало алгебраических проблем. Указал знакомую теперь всем геометрическую модель комплексных чисел и действий с ними.
Гаусс дал классическую теорию сравнений, открыл конечное поле вычетов по простому модулю, глубоко проник в свойства вычетов.

ПОЯСНЕНИЕ
К ТЕРМИНАМ
Кольцо- в ней определены операции обратимого сложения и операция умножения, по свойствам похожие на соответствующие операции над числами.
Гауссовы целые числа (гауссовы числа, целые комплексные числа)- это комплексные числа, у которых как вещественная, так и мнимая часть — целые числа. Пример:
Впервые введены Гауссом в монографии «Теория биквадратичных вычетов» (1828—1832). Множество гауссовых целых чисел принято обозначать Z [i], отражая тем самым тот факт, что оно получается из множества целых чисел Z добавлением в него мнимой единицы i и комбинаций её с целыми числами. Свойства гауссовых чисел похожи на свойства обычных целых чисел, однако имеются и существенные отличия.

ПОЯСНЕНИЕ
К ТЕРМИНАМ №2
Дели́мость — одно из основных понятий арифметики и теории чисел, связанное с операцией деления. С точки зрения теории множеств, делимость целых чисел является отношением, определённым на множестве целых чисел.