Слайд 2План
Понятие вектора
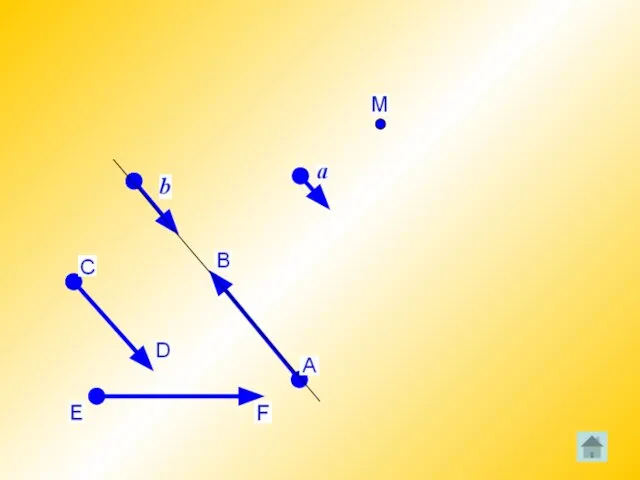
Определение
Нулевой вектор
Длина (модуль) вектора
Равенство векторов
Коллинеарные векторы
Сонаправленные и противоположно направленные векторы
Определение

Слайд 3Понятие вектора
Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не

только своим числовым значением, но и направлением в пространстве.
Такие физические величины называются векторными величинами
(или коротко векторами).
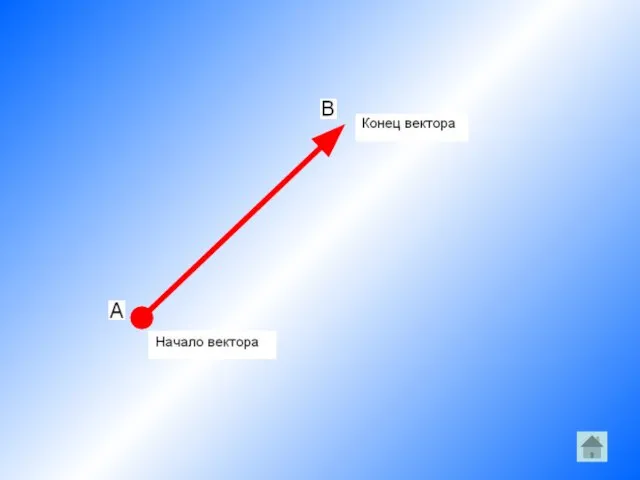
Слайд 4Определение
Отрезок, для которого указано,
какая из его граничных точек считается началом, а

какая- концом, называется направленным отрезком или вектором.
Слайд 8Нулевой вектор
Любая точка плоскости также является вектором. В этом случае вектор называется
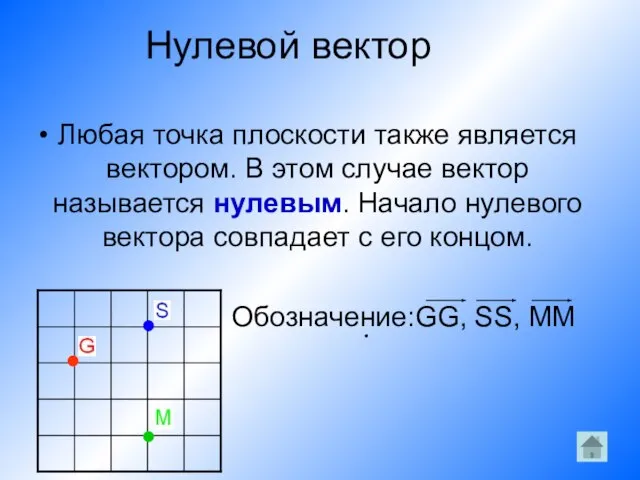
нулевым. Начало нулевого вектора совпадает с его концом.
Обозначение:GG, SS, MM
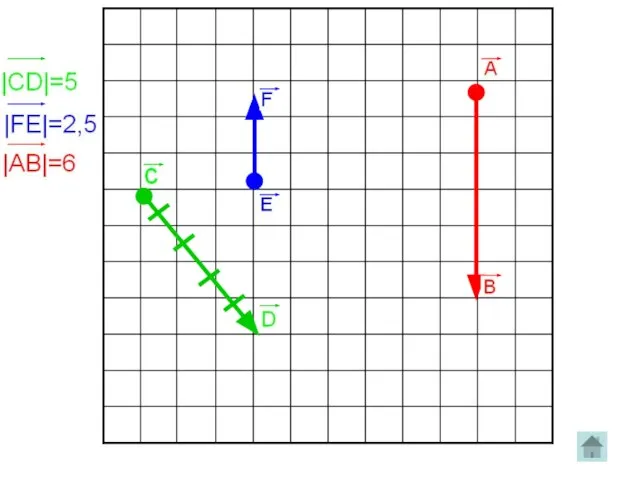
Слайд 9Длина вектора
Длиной или модулем ненулевого вектора AB называется длина отрезка AB. Длина

вектора AB (вектора a) обозначается так: AB (|a|). Длина нулевого вектора считается равной нулю: |0|=0
Слайд 10Равенство векторов
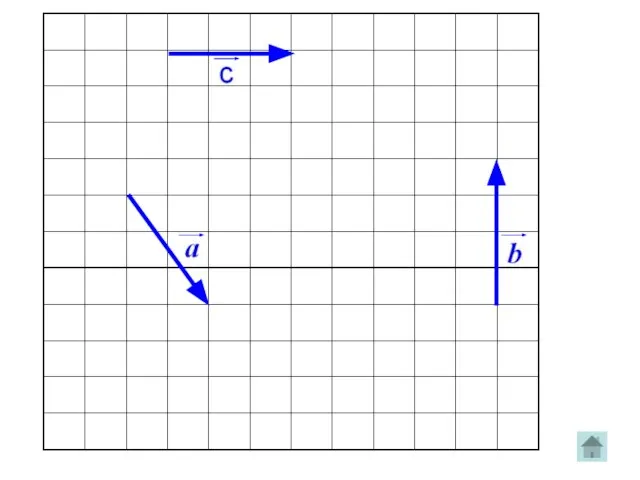
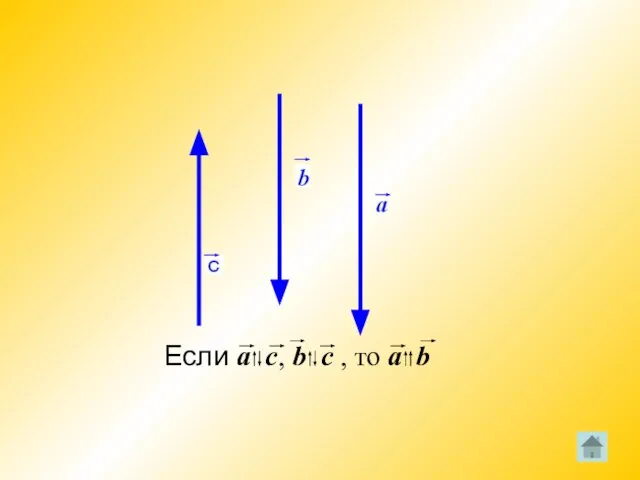
Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если они лежат либо на одной

прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору.
Слайд 12Сонаправленные и противоположно направленные векторы
Если два ненулевых вектора a и b

коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы a и b называются сонаправленными(a b), а во втором- противоположно направленными (a b).
Слайд 16Определение
Векторы называются равными(a b), если они сонаправлены и их длины равны.








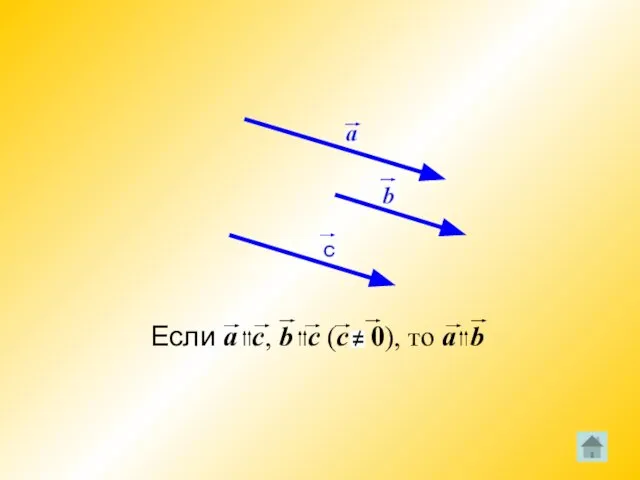


 Шахматы и математика
Шахматы и математика Точка перегиба
Точка перегиба Интегрированный урок (алгебра + физика). Действия со степенями 8 класс
Интегрированный урок (алгебра + физика). Действия со степенями 8 класс Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Деление
Деление Углы
Углы Этапы построения эконометрических моделей
Этапы построения эконометрических моделей Космические тропинки. Урок-игра по математике
Космические тропинки. Урок-игра по математике Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций Решение задачи описательной статистики в Mathcad
Решение задачи описательной статистики в Mathcad Решение задач на проценты
Решение задач на проценты Решение уравнений. Первый и второй уровни
Решение уравнений. Первый и второй уровни Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4
Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4 Тригонометрические функции. Их свойства и график (1)
Тригонометрические функции. Их свойства и график (1) Цена деления измерительных приборов
Цена деления измерительных приборов Математика и физика здоровья
Математика и физика здоровья Кривая производственных возможностей
Кривая производственных возможностей ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Геометрия Евклида
Геометрия Евклида Теоретические аспекты математического анализа
Теоретические аспекты математического анализа аксіоми стереометрії
аксіоми стереометрії Признаки равенства треугольников
Признаки равенства треугольников 8c3f0c24-2702-4093-8e3e-0619d16772a5
8c3f0c24-2702-4093-8e3e-0619d16772a5 865f4a04-e6d6-4374-8401-b49cfc41ea6e
865f4a04-e6d6-4374-8401-b49cfc41ea6e Евклидова геометрия
Евклидова геометрия Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Конструктивная геометрия. Лекция 5. Метрические задачи
Конструктивная геометрия. Лекция 5. Метрические задачи