Содержание
- 2. Возведение трёхчлена в квадрат
- 3. Мы знаем как возвести в квадрат сумму двух слагаемых. Но почему только двух? Увеличим число слагаемых
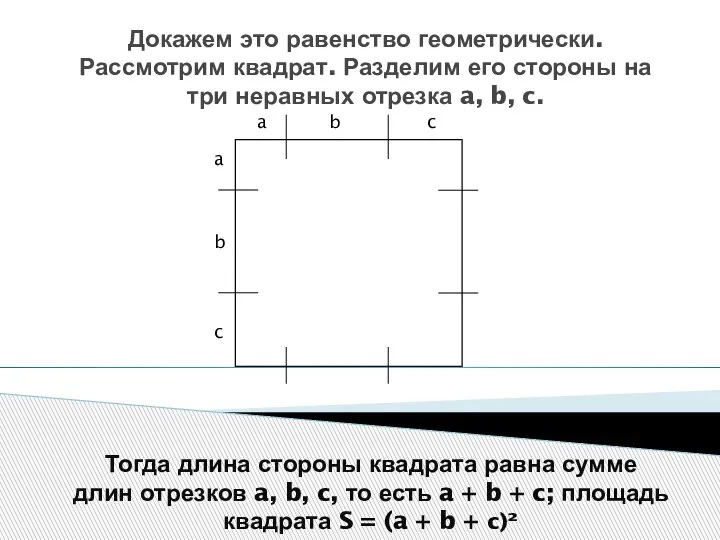
- 4. Докажем это равенство геометрически. Рассмотрим квадрат. Разделим его стороны на три неравных отрезка a, b, c.
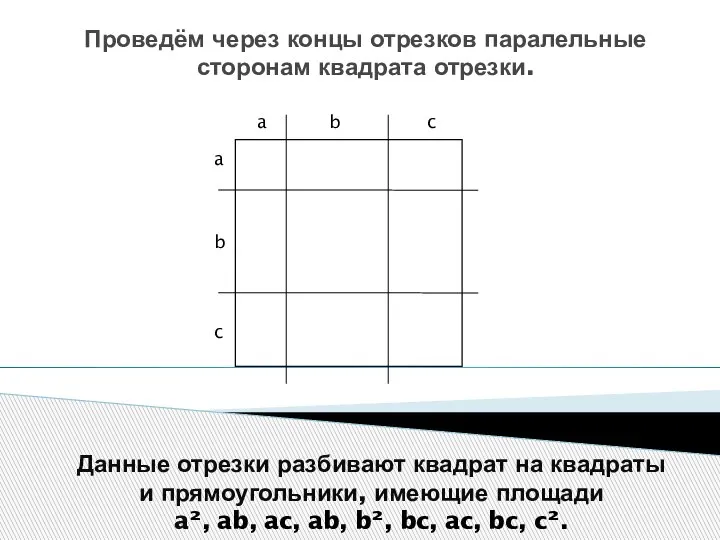
- 5. Проведём через концы отрезков паралельные сторонам квадрата отрезки. Данные отрезки разбивают квадрат на квадраты и прямоугольники,
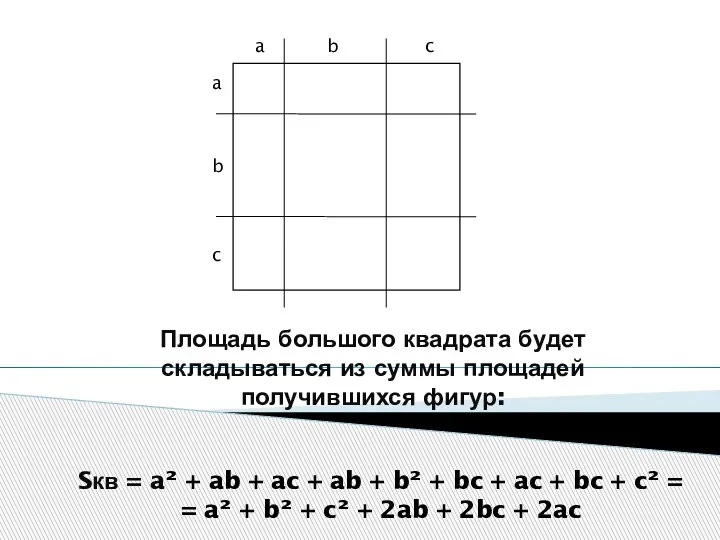
- 6. Площадь большого квадрата будет складываться из суммы площадей получившихся фигур: a a b b c c
- 8. Скачать презентацию


 Презентация на тему Векторы
Презентация на тему Векторы  Геометрический калейдоскоп
Геометрический калейдоскоп Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Кубический корень
Кубический корень Треугольник и квадранты. Тестирования. Основные понятия
Треугольник и квадранты. Тестирования. Основные понятия Проценты. Устная работа
Проценты. Устная работа Презентация на тему Округление натуральных чисел
Презентация на тему Округление натуральных чисел  SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY Производная функции. Геометрический смысл производной
Производная функции. Геометрический смысл производной Математический турнир Умники и умницы
Математический турнир Умники и умницы Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Способы построения параллельных прямых
Способы построения параллельных прямых Презентация на тему Площадь круга и кругового сектора
Презентация на тему Площадь круга и кругового сектора  Приём вычитания вида 12 -
Приём вычитания вида 12 - Формулы половинного аргумента
Формулы половинного аргумента Гипотеза Коллатца. (доказательство гипотезы)
Гипотеза Коллатца. (доказательство гипотезы) Коэффициент. Упрощение выражений
Коэффициент. Упрощение выражений Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла Powtórzenie do klasówki
Powtórzenie do klasówki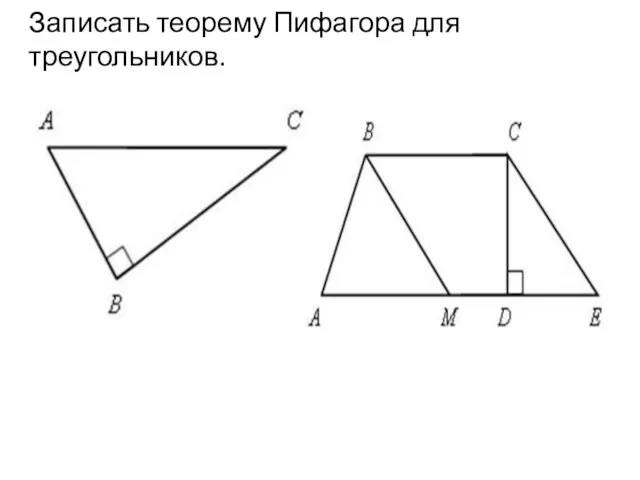 Теорема Пифагора. Урок 24
Теорема Пифагора. Урок 24 Статистические таблицы и графики
Статистические таблицы и графики Логарифмы. Тест по алгебре
Логарифмы. Тест по алгебре Сравнение, сложение и вычитание обыкновенных дробей. 6 класс
Сравнение, сложение и вычитание обыкновенных дробей. 6 класс Письменные приемы вычислений
Письменные приемы вычислений Спектральное представление ССП
Спектральное представление ССП Признаки равенства треугольников. Равнобедренный треугольник. Задачи по готовым чертежам
Признаки равенства треугольников. Равнобедренный треугольник. Задачи по готовым чертежам Булева алгебра. Классы булевых функций. Шаблон решения контрольной работы
Булева алгебра. Классы булевых функций. Шаблон решения контрольной работы Презентация по математике "Использование информационных технологий в преподавании математики" -
Презентация по математике "Использование информационных технологий в преподавании математики" -