Вписанная и описанная окружности

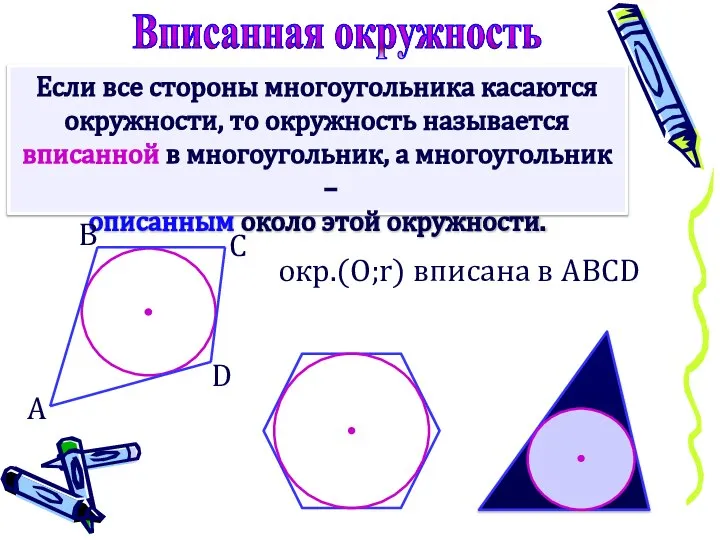
Если все стороны многоугольника касаются
окружности, то окружность называется
вписанной в многоугольник, а многоугольник –
описанным около этой окружности.
Вписанная окружность
А
В
С
D
окр.(О;r) вписана в ABCD

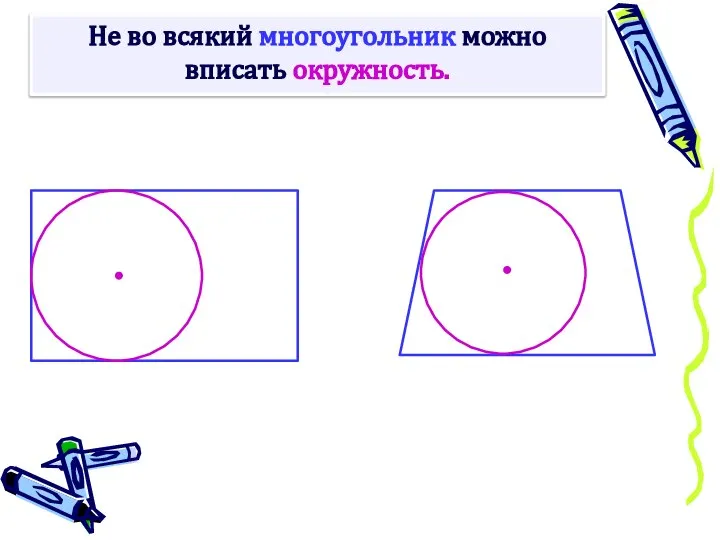
Не во всякий многоугольник можно вписать окружность.

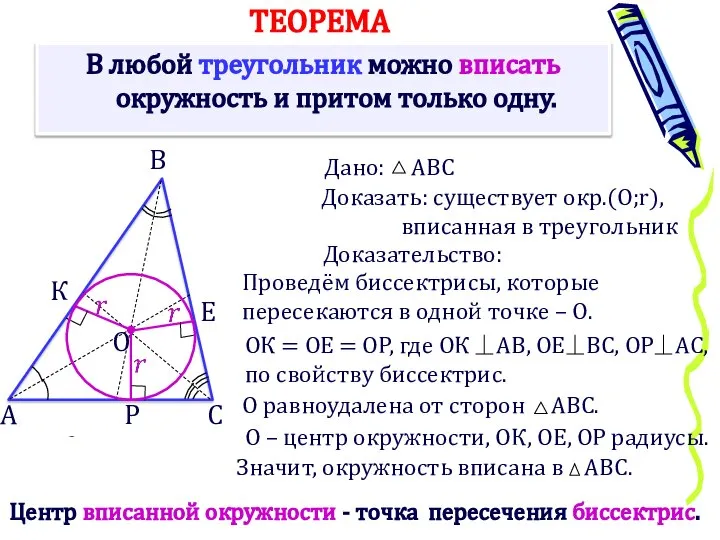
В любой треугольник можно вписать окружность и притом только одну.
А
Доказать: существует окр.(О;r), вписанная в треугольник
Доказательство:
Проведём биссектрисы, которые пересекаются в одной точке – О.
ОК = ОЕ = ОР, где ОК АВ, ОЕ ВС, ОР АС, по свойству биссектрис.
О – центр окружности, ОК, ОЕ, ОР радиусы.
ТЕОРЕМА
В
С
О
К
Е
Р
Центр вписанной окружности - точка пересечения биссектрис.

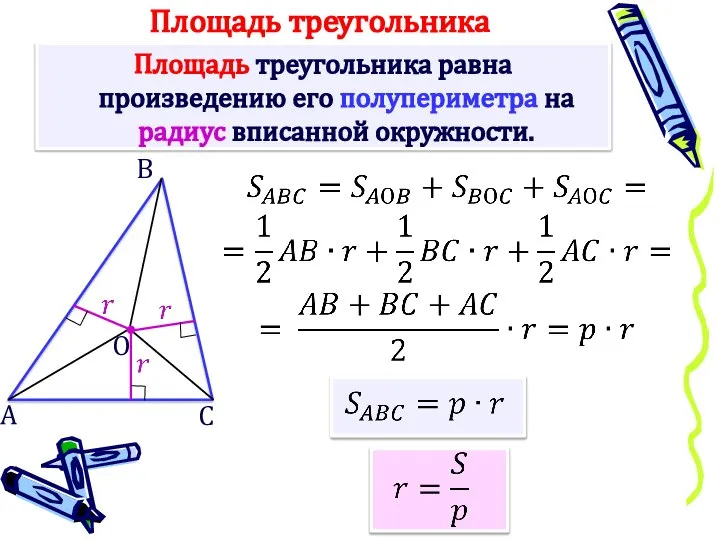
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
А
Площадь треугольника

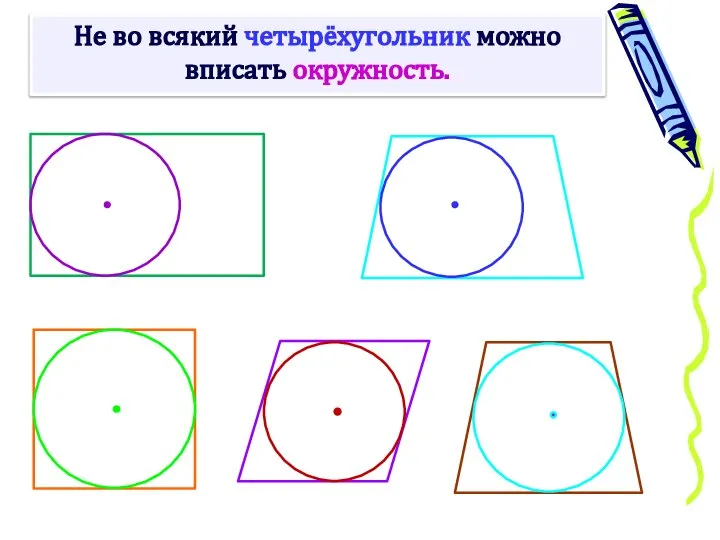
Не во всякий четырёхугольник можно вписать окружность.

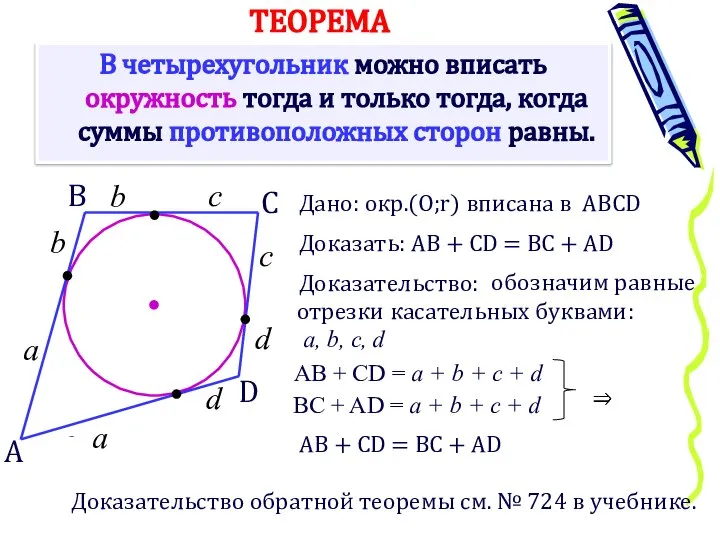
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны.
ТЕОРЕМА
А
В
С
D
Дано: окр.(О;r) вписана в ABCD
Доказательство:
Доказать: AB + CD = BC + AD
a
a
b
b
c
c
d
d
AB + CD = a + b + c + d
BC + AD = a + b + c + d
AB + CD = BC + AD
Доказательство обратной теоремы см. № 724 в учебнике.
обозначим равные
отрезки касательных буквами:
а, b, c, d

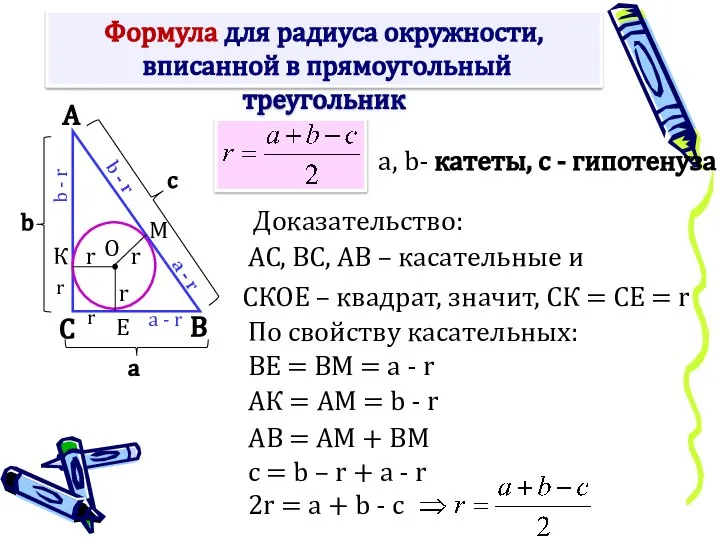
Формула для радиуса окружности,
вписанной в прямоугольный треугольник
Доказательство:
СКОЕ – квадрат, значит, СК = СЕ = r
По свойству касательных:
ВЕ = ВМ = а - r
АК = АМ = b - r
AB = AM + BM
c = b – r + a - r
2r = a + b - c
АС, ВС, АВ – касательные и
r
r
b - r
а - r
b - r
а - r

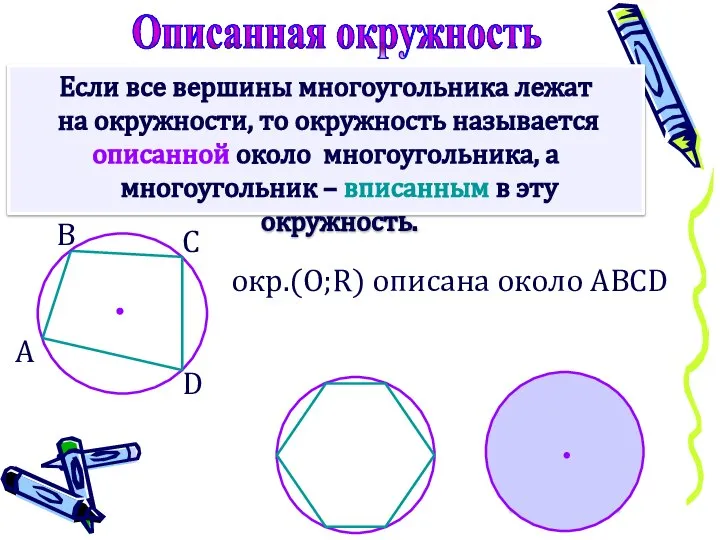
Если все вершины многоугольника лежат
на окружности, то окружность называется
описанной около многоугольника, а многоугольник – вписанным в эту окружность.
Описанная окружность
окр.(О;R) oписана около ABCD
А
В
С
D

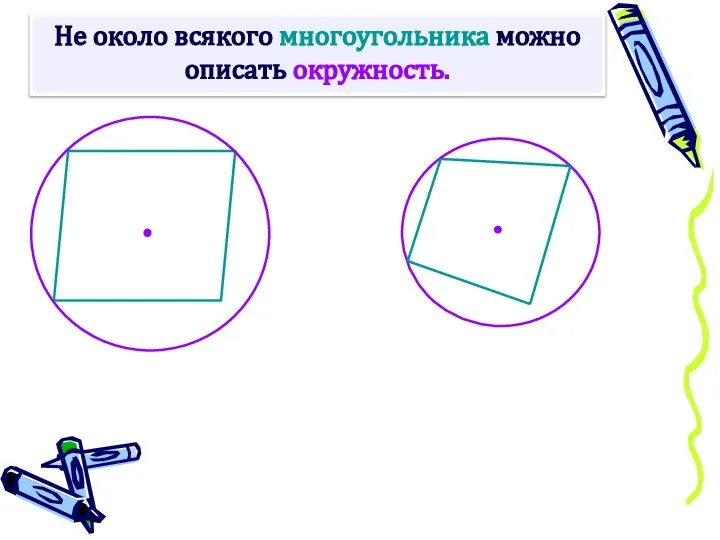
Не около всякого многоугольника можно описать окружность.

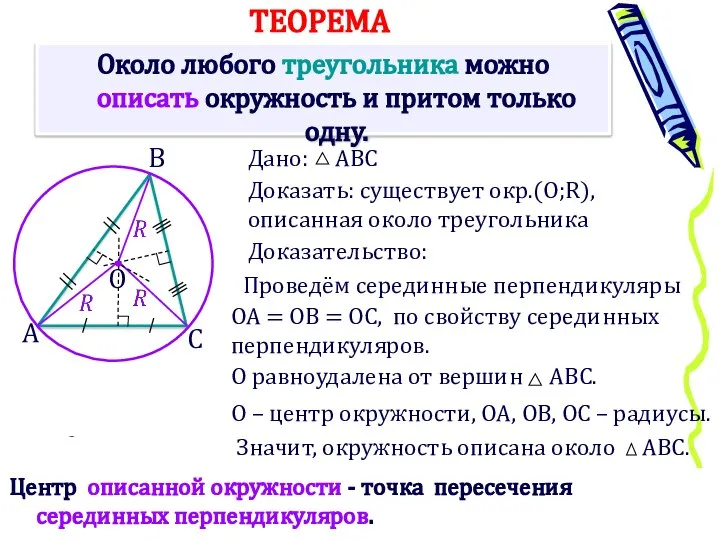
Около любого треугольника можно описать окружность и притом только одну.
Доказать: существует окр.(О;R),
описанная около треугольника
Доказательство:
Проведём серединные перпендикуляры
ОА = ОВ = ОС, по свойству серединных перпендикуляров.
О – центр окружности, ОА, ОВ, ОС – радиусы.
ТЕОРЕМА
А
В
С
О
Центр описанной окружности - точка пересечения серединных перпендикуляров.

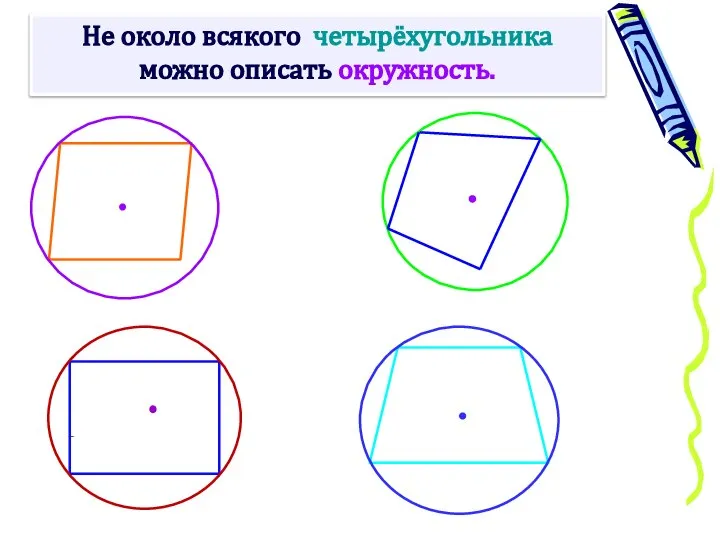
Не около всякого четырёхугольника можно описать окружность.