Теория вероятностей и математическая статистика

Перестановками называются размещения из n элементов по n
Сочетаниями из n элементов по k называются выборки на множестве
из n элементов по k ( k < n ) без учёта порядка.
Число сочетаний на множестве из
n элементов по k равно

Cлучайные события и их классификация.
Методами теории вероятностей изучаются явления, которые могут происходить при воспроизведении одних и тех же условий (при экспериментах, опытах, испытаниях) и обладают свойством «статистической устойчивости».
Событием (случайным) называется всякий факт, который может либо произойти, либо нет в результате неоднократного проведения одного и того же опыта. Примерами событий могут служить: 1. Попадание в цель при выстреле из орудия (опыт-стрельба, событие – попадание в цель). 2. Выпадение двух гербов при трёхкратном подбрасывании монеты (опыт - бросание монеты, событие - выпадение двух гербов).

Достоверным называется событие, которое обязательно происходит в результате данного эксперимента.
Невозможным называется событие которое не может произойти в результате данного эксперимента

Пространством элементарных событий называется множество Ω, содержащее все возможные исходы данного эксперимента, из которых в результате испытания может реализоваться только один исход.

Классическая вероятность
Вероятностью события А называется отношение числа m
благоприятствующих появлению этого события исходов
опыта m к числу всех возможных исходов n:

Статистическая и геометрическая вероятности

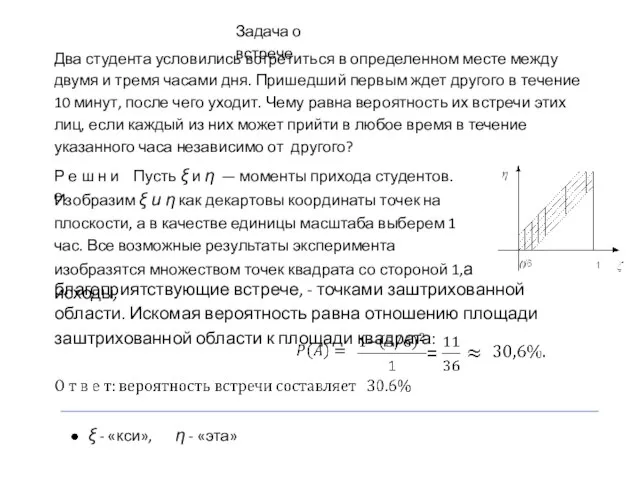
ξ - «кси»,
η - «эта»
Задача о встрече
Два студента условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность их встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
Р е ш н и е.
Пусть ξ и η — моменты прихода студентов. Изобразим ξ и η как декартовы координаты точек на плоскости, а в качестве единицы масштаба выберем 1 час. Все возможные результаты эксперимента изобразятся множеством точек квадрата со стороной 1,а исходы,
благоприятствующие встрече, - точками заштрихованной области. Искомая вероятность равна отношению площади заштрихованной области к площади квадрата:

Основные аксиомы теории вероятностей
Тогда p = 1- q = 1-0.207=0.793

Условная вероятность. Правило умножения вероятностей

Теорема сложения вероятностей

Замечание. Практически часто удобно вычислять вероятность суммы событий через вероятности произведения противоположных событий по формуле
Пример.

Формула полной вероятности
Формула Бейеса

Пример.

Формула Бернулли
.

Понятие случайной величины.
Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.
Примеры непрерывных случайных величин:
Случайное отклонение X по дальности точки падения снаряда от цели (так как снаряд может упасть в любую точку интервала, ограниченного пределами рассеяния снарядов, то все числа из этого интервала будут возможными значениями X)
2. Время безотказной работы радиолампы.

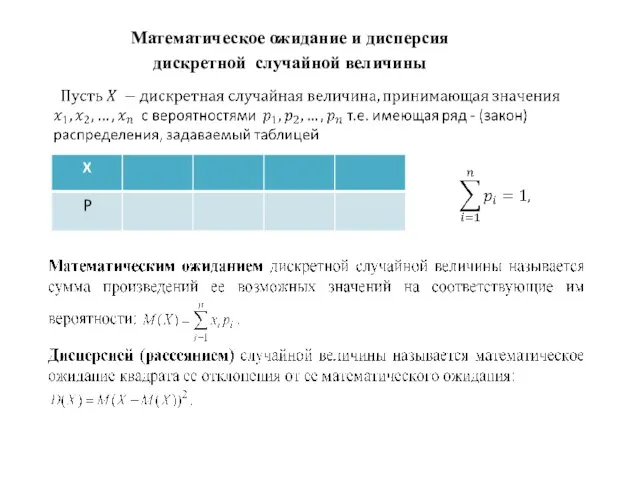
Математическое ожидание и дисперсия
дискретной случайной величины

Задача. Дискретная случайная величина Х имеет только два возможных значения: х1 и х2, причем х1< x2 . Найти закон распределения величины Х, если известно, что вероятность того, что Х примет значение х1, равна P1 = 0.6 , а М(Х) = 1.4; D(Х) = 0.24.
Р е ш е н и е. Разобьём ход решения задачи на два этапа
1этап.
Найдём вероятность p 2 того, что Х примет значение х2.
Сумма вероятностей всех возможных значений Х равна единице

2 шаг. Решив систему уравнений
найдем два решения: х1= 1, х2 = 2 и х1= 1.8, х2 = 0.8.
По условию х1< х2 , поэтому задаче удовлетворяет только первое решение.
О т в е т: искомый закон
распределения имеет вид:

Плотность распределения, математическое ожидание и дисперсия непрерывной случайной величины.
Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х: F (x) = p (X < x).
Свойства функции распределения.
Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле:
f (x) = F′(x).
Свойства функции плотности распределения.
Математическое ожидание непрерывной
случайной величины
Дисперсия непрерывной случайной величины

Задача. Найти плотность распределения вероятностей,
математическое ожидание и дисперсию случайной
величины Х, заданной функцией распределения
Р е ш е н и е.
Найдем плотность распределения вероятностей
по формуле
Найдём математическое ожидания величины по формуле
Дисперсию непрерывной случайной величины находим по формуле:
f (x) = F′(x). = >

Нормальный закон распределения

Известны математическое ожидание m= 10 и среднее квадратичное отклонение σ = 2 нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (12,14).
Р е ш е н и е.
Подставим α = 12, β = 14, а = 10 и σ = 2 в формулу
Р(12 < X < 14) = Ф(2) – Ф(1)
Значения Ф(2) и Ф(1) функции Лапласа находим по таблице, которая приводится в приложении учебников и справочников по теории вероятностей:
Ф(2) = 0.4772; Ф(1) = 0.3413. = >
Р(12 < X < 14) = 0.4772 - 0.3413 = 0.1359
Р(12 < X < 14) = 0.1359.
Задача.