Содержание
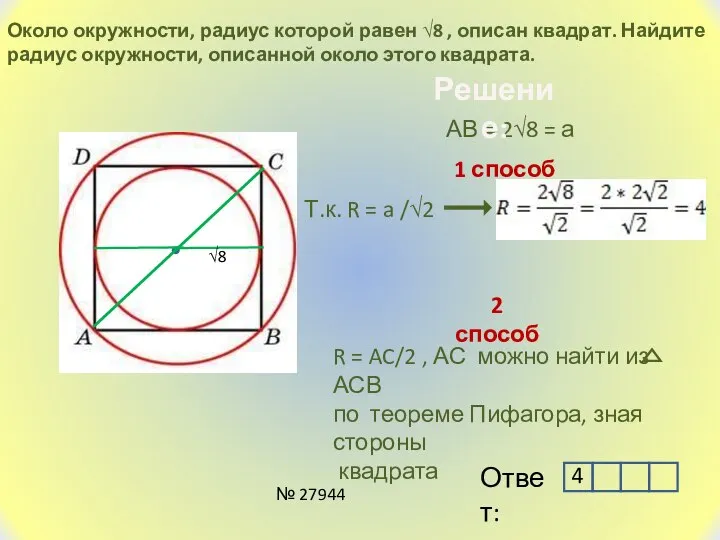
- 2. Около окружности, радиус которой равен √8 , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
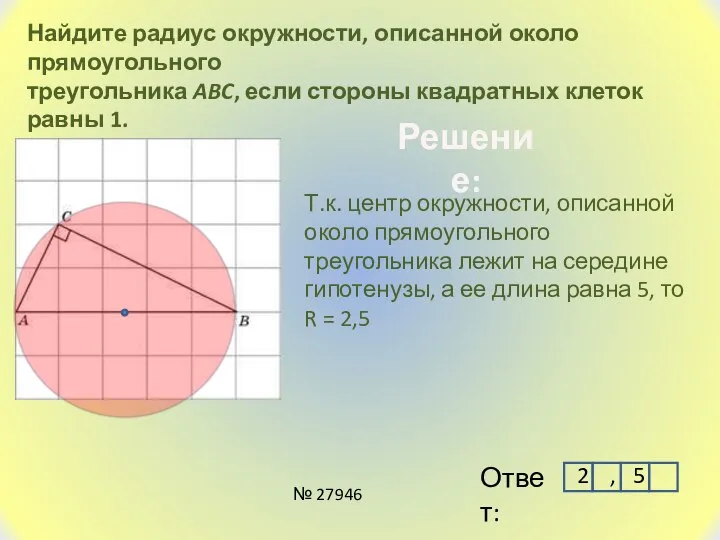
- 3. Найдите радиус окружности, описанной около прямоугольного треугольника ABC, если стороны квадратных клеток равны 1. Т.к. центр
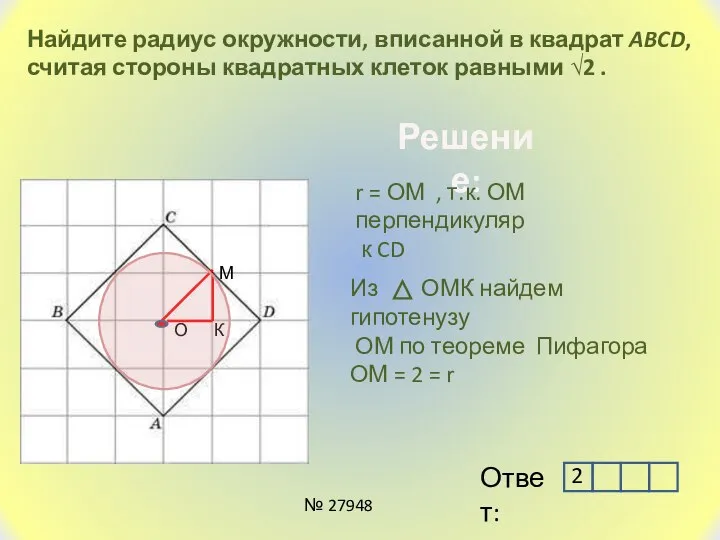
- 4. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными √2 . Решение: r
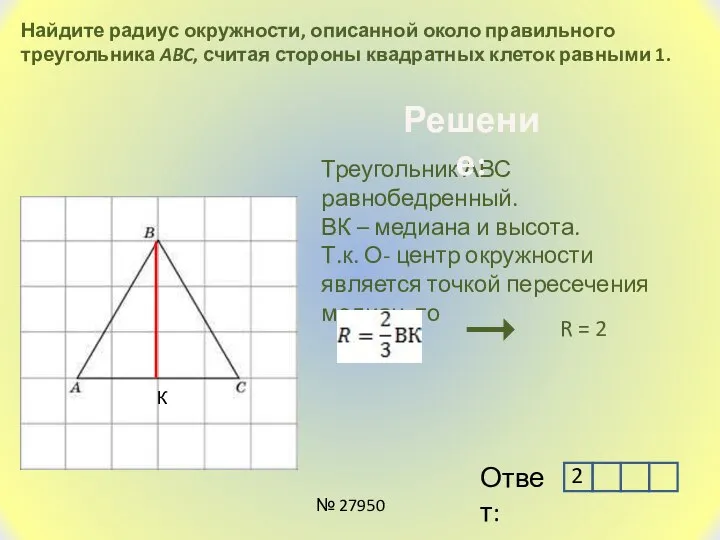
- 5. Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1. К Треугольник
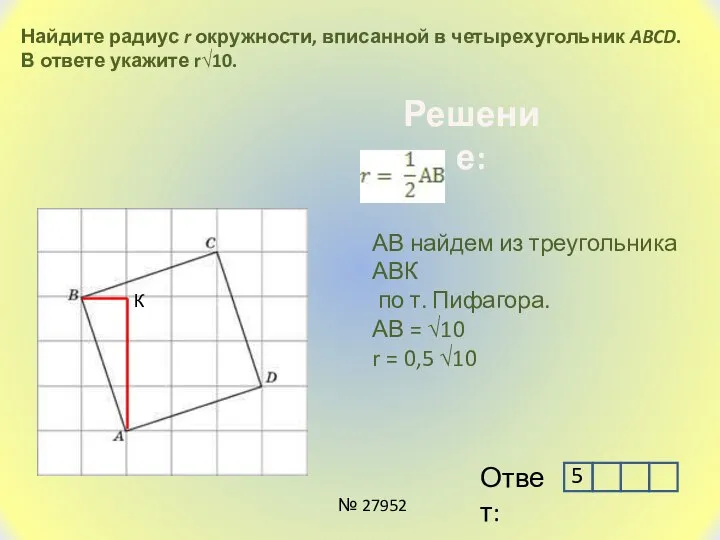
- 6. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите r√10. АВ найдем из треугольника
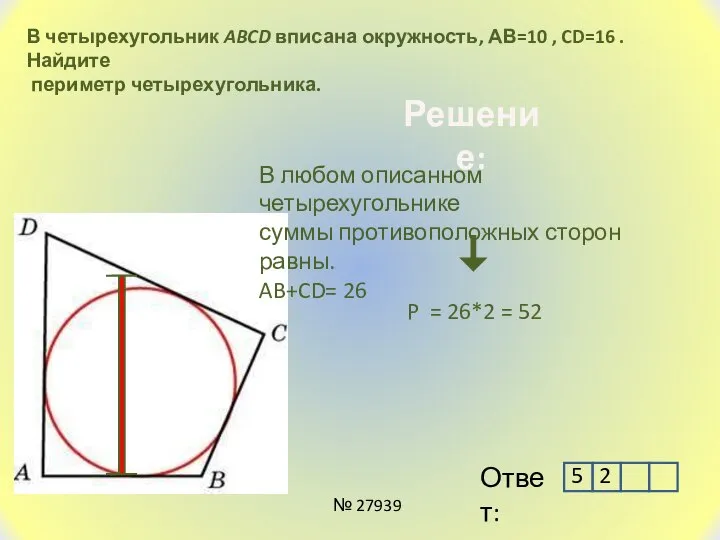
- 7. В четырехугольник ABCD вписана окружность, АВ=10 , CD=16 . Найдите периметр четырехугольника. Решение: В любом описанном
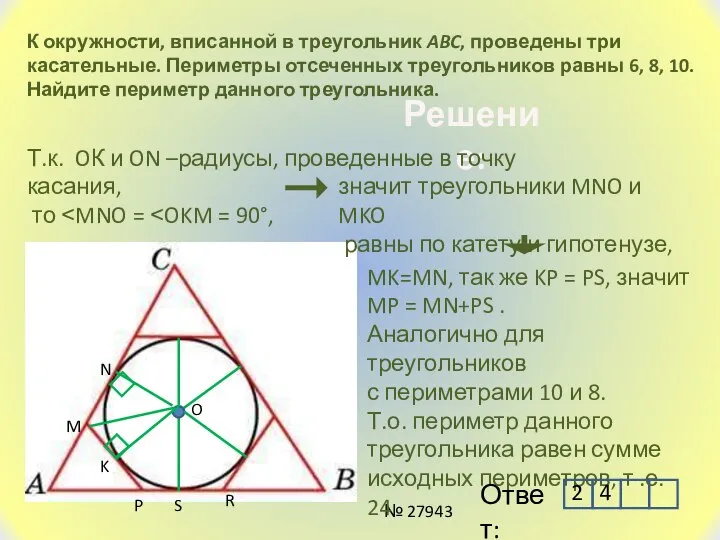
- 8. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10.
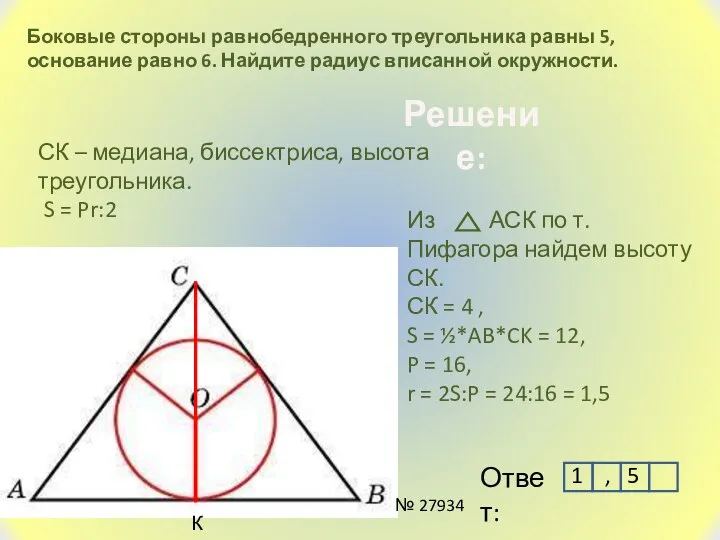
- 9. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности. К Решение: СК
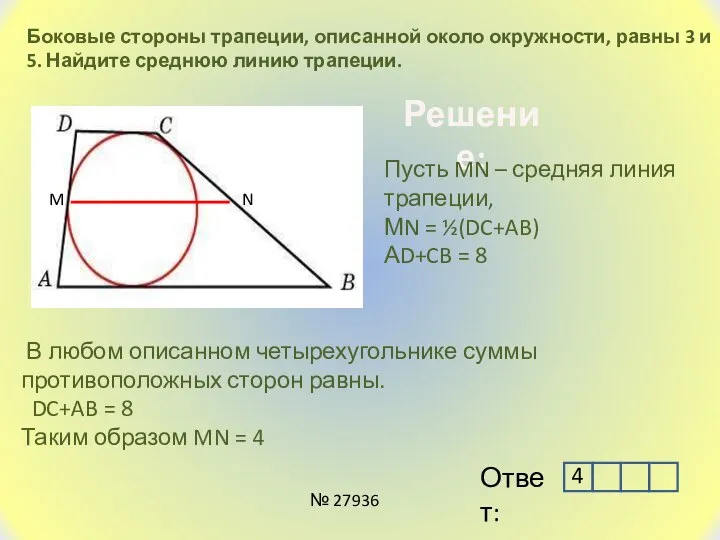
- 10. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции. Решение: В
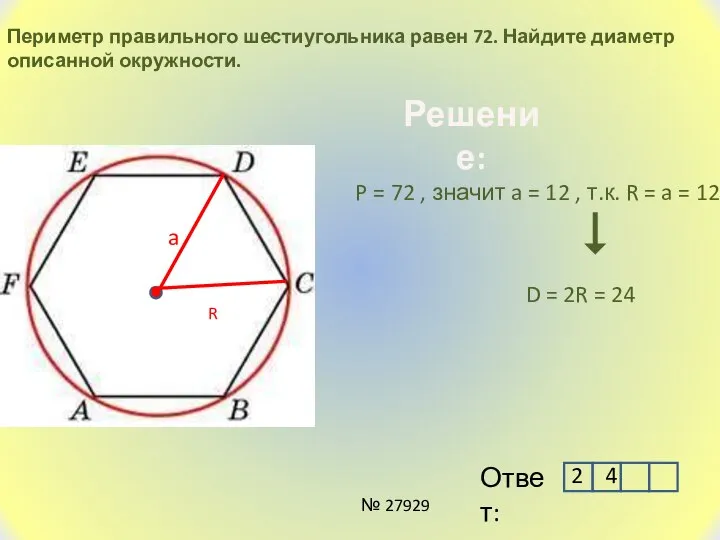
- 11. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности. Решение: P = 72 , значит a
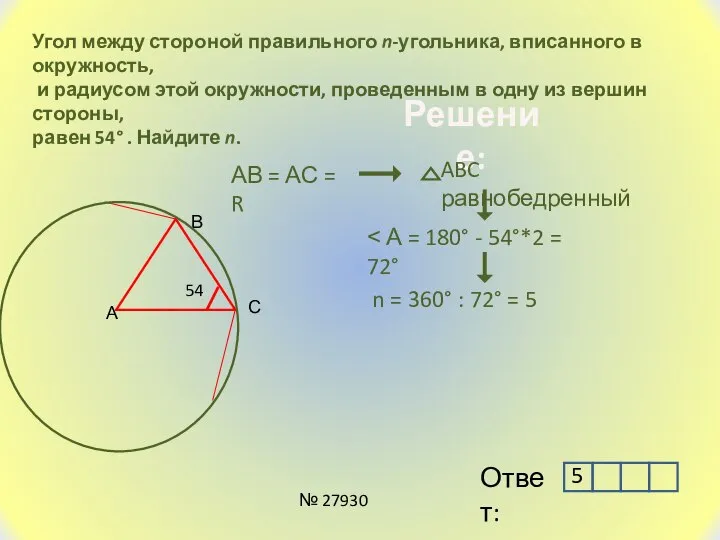
- 12. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из
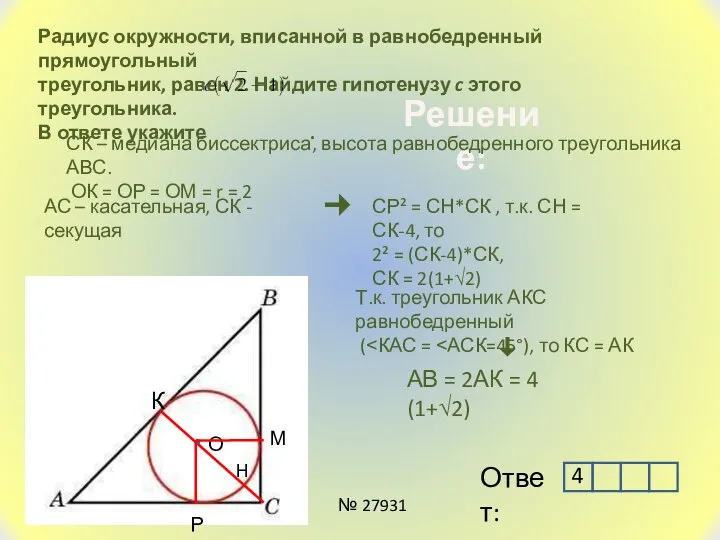
- 13. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе
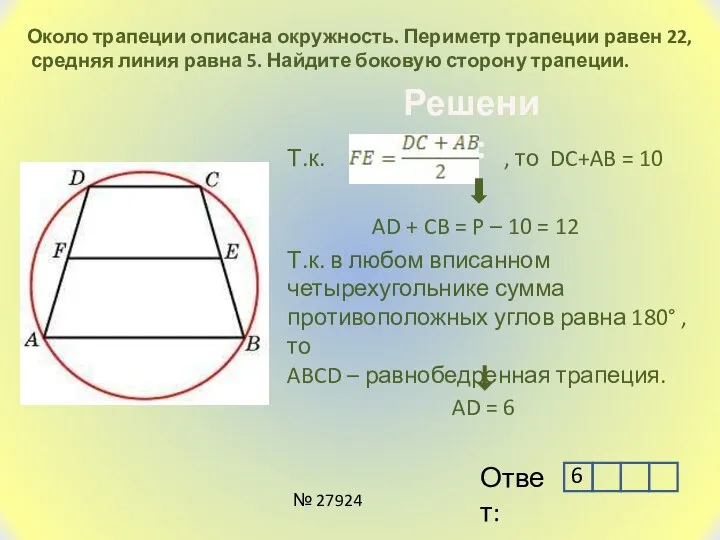
- 14. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
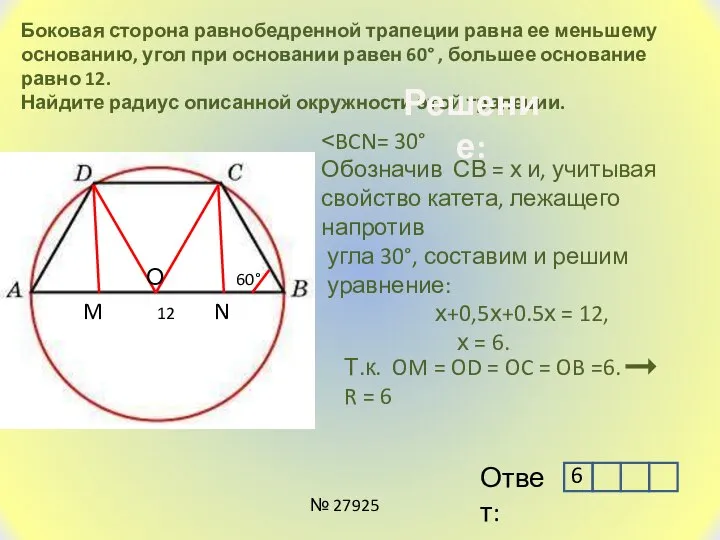
- 15. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60° , большее основание
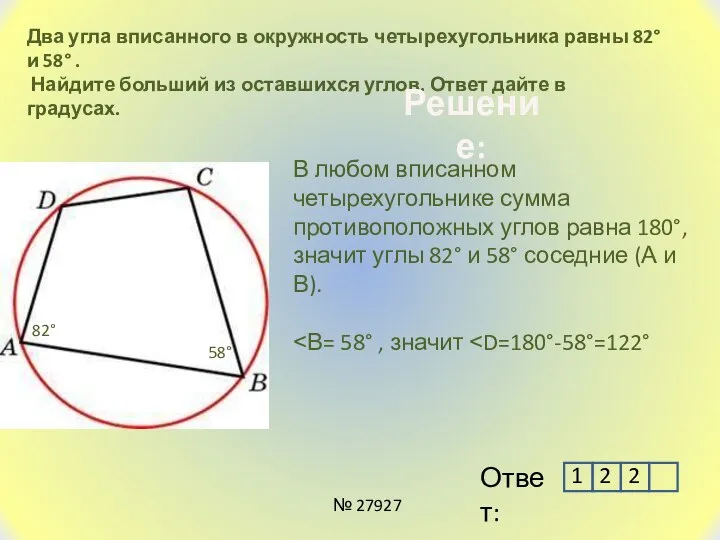
- 16. Два угла вписанного в окружность четырехугольника равны 82° и 58° . Найдите больший из оставшихся углов.
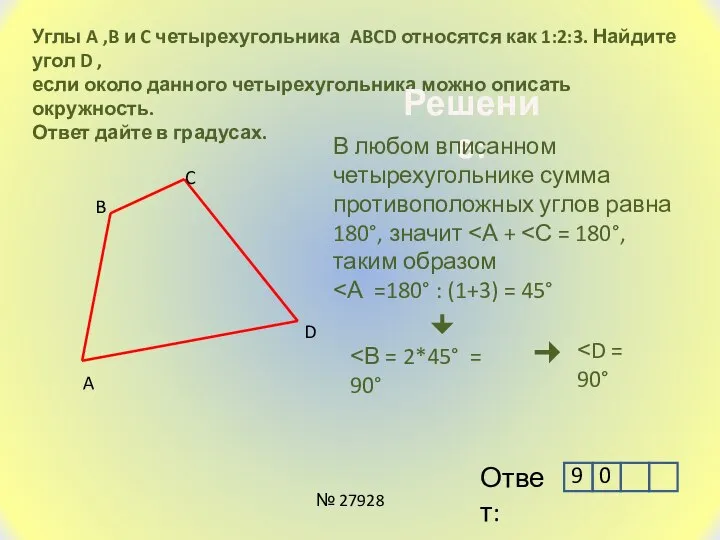
- 17. Углы A ,B и C четырехугольника ABCD относятся как 1:2:3. Найдите угол D , если около
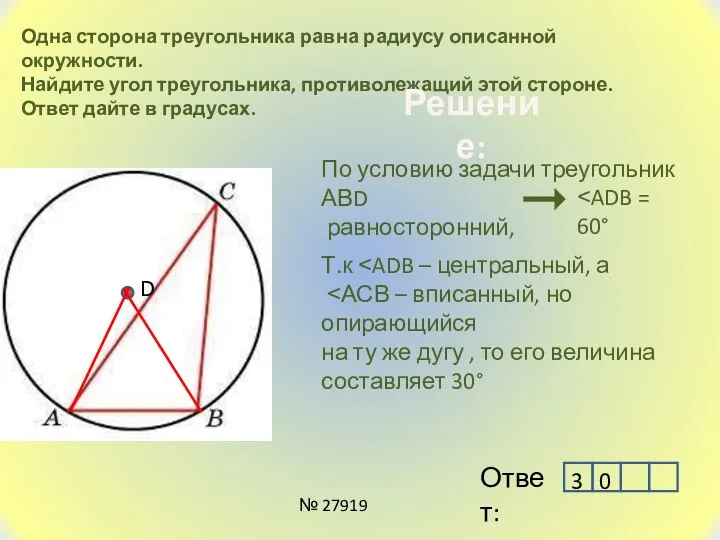
- 18. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в
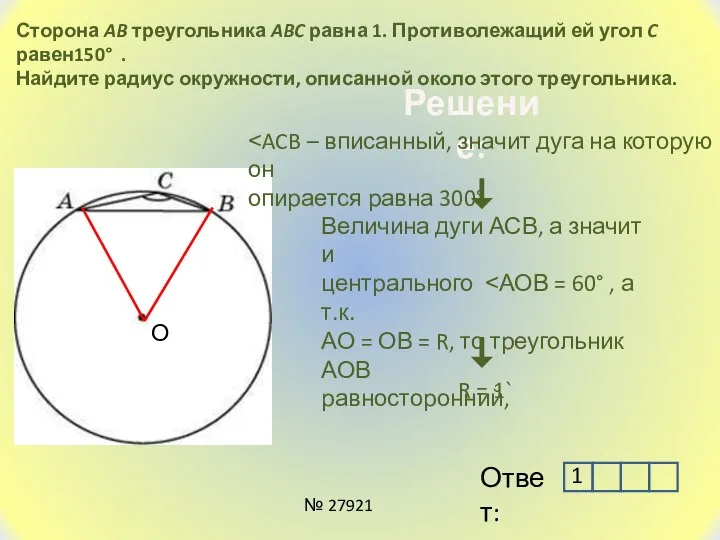
- 19. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен150° . Найдите радиус окружности, описанной
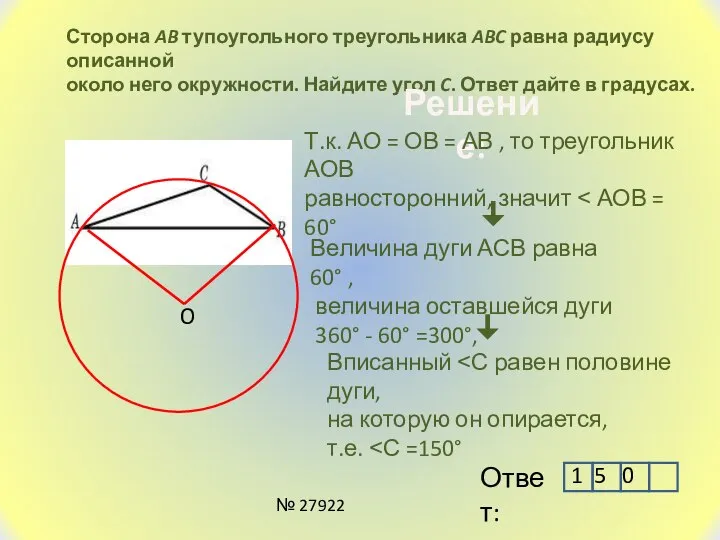
- 20. Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте
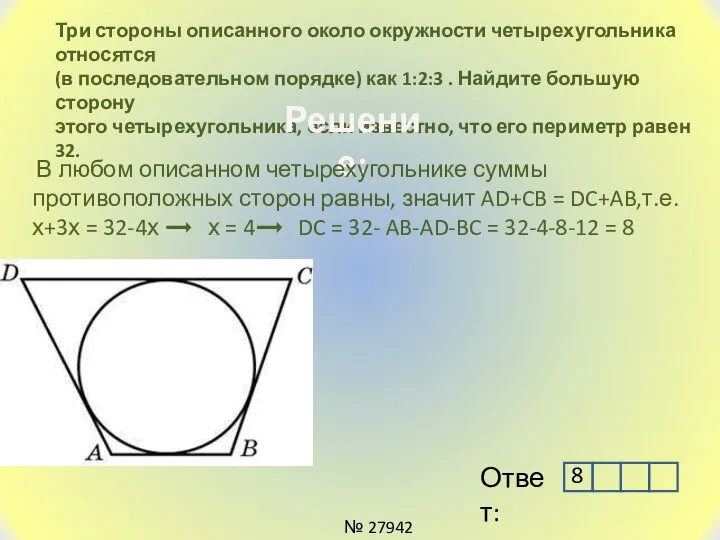
- 21. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3 . Найдите большую сторону
- 23. Скачать презентацию
 Частное и его значение
Частное и его значение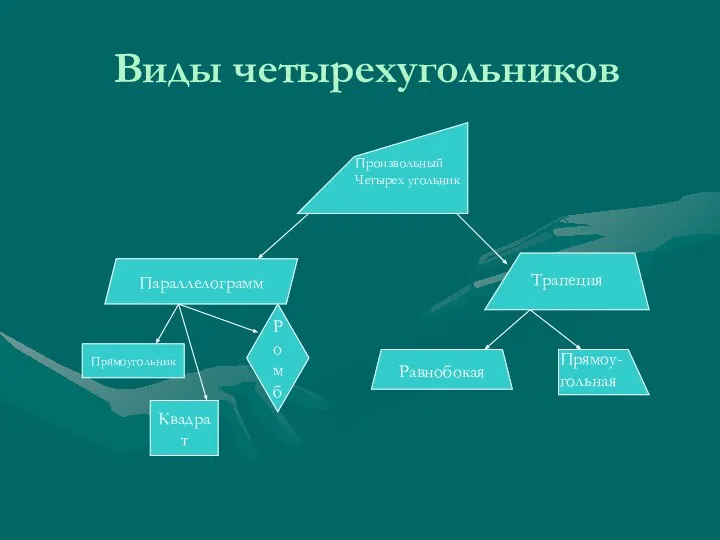 Виды четырехугольников
Виды четырехугольников Процентное содержание компонентов
Процентное содержание компонентов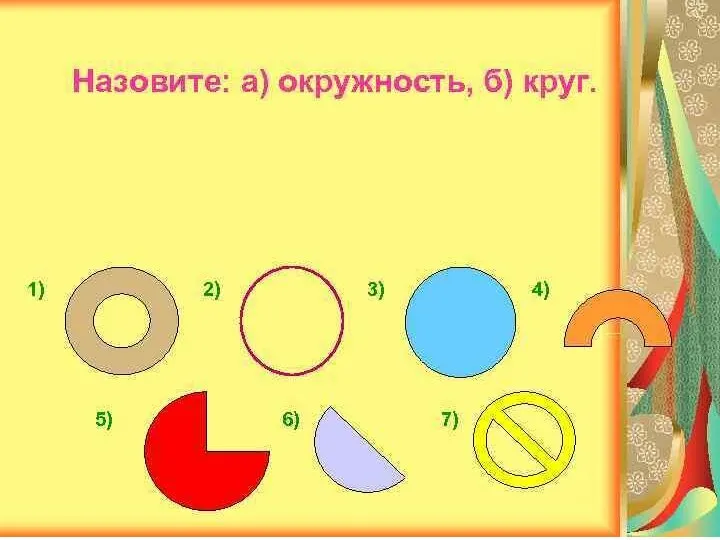 Окружность
Окружность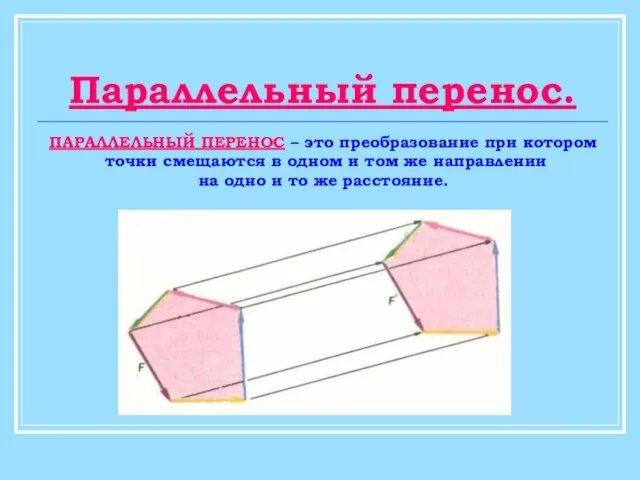 Параллельный перенос фигур
Параллельный перенос фигур Сущность экономического прогнозирования
Сущность экономического прогнозирования первые уроки геометрии
первые уроки геометрии Показательные неравенства
Показательные неравенства Стандартный вид числа
Стандартный вид числа Таблица сложения
Таблица сложения Окружность, круг, их элементы и части. Центральный угол. 7 класс
Окружность, круг, их элементы и части. Центральный угол. 7 класс Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Какую прямую называют координатной?
Какую прямую называют координатной? Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Презентация на тему Теорема синусов
Презентация на тему Теорема синусов  Теорема о неполноте
Теорема о неполноте Презентация на тему Технологии развивающего обучения в практике учителя математики
Презентация на тему Технологии развивающего обучения в практике учителя математики  Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Проект Математическая вертикаль. Геометрия. 8 класс
Проект Математическая вертикаль. Геометрия. 8 класс Задача з піцою
Задача з піцою Презентация на тему Место числового множителя в выражении с переменной
Презентация на тему Место числового множителя в выражении с переменной  Разложение функций в степенные ряды
Разложение функций в степенные ряды Иррациональные уравнения
Иррациональные уравнения Умножение
Умножение Геометрия в искусстве
Геометрия в искусстве Что такое дискретная математика?
Что такое дискретная математика? Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график סדר פעולות החשבון
סדר פעולות החשבון