Содержание
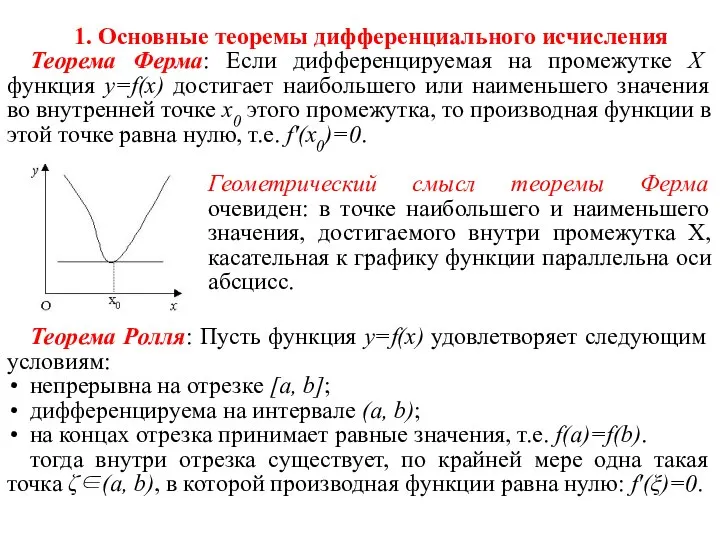
- 2. 1. Основные теоремы дифференциального исчисления Теорема Ферма: Если дифференцируемая на промежутке Х функция y=f(x) достигает наибольшего
- 3. Геометрический смысл теоремы Ролля: найдется хотя бы одна точка, в которой касательная к графику функции будет
- 4. 2. Правило Лопиталя Правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу
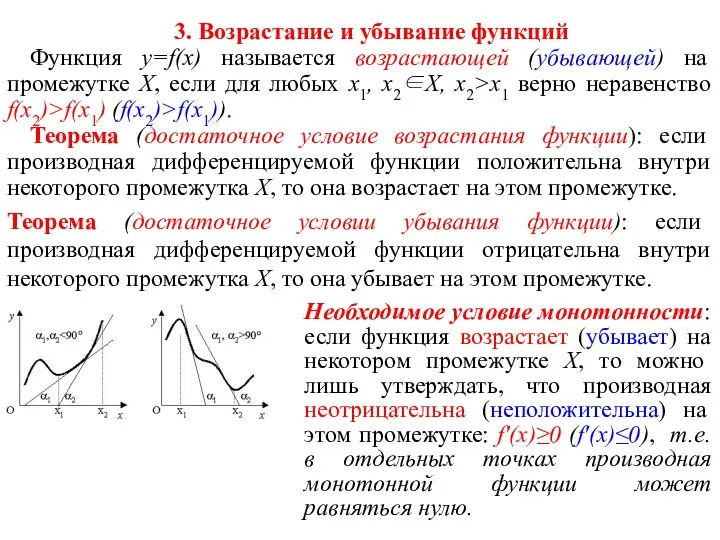
- 5. 3. Возрастание и убывание функций Функция y=f(x) называется возрастающей (убывающей) на промежутке Х, если для любых
- 6. 4. Экстремум функции Рассмотрим график некоторой функции f(x). На этом графике мы имеем последовательное чередование промежутков
- 7. Значения функции в точках х0 и х1 называются соответственно максимумом и минимумом функции. Максимумы и минимумы
- 8. Теорема 2: если первая производная f′(x) дважды дифференцируемой функции f(x) равна нулю в некоторой точке х0,
- 9. Пример. Найти экстремумы функции y=x3-3x2-4. Решение. 1. Находим первую производную y′=3x2-6x=3x(x-2). 2. Находим критические точки из
- 10. Пример. Капитал в 1 млн. руб. может быть размещен в банке по 50% годовых или инвестирован
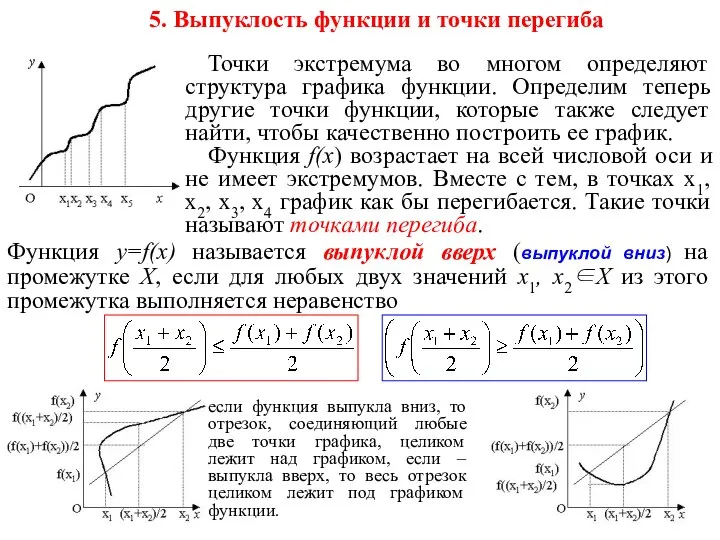
- 11. Точки экстремума во многом определяют структура графика функции. Определим теперь другие точки функции, которые также следует
- 12. Достаточное условие выпуклости функции вниз (вверх) диктуется следующей теоремой: Если вторая производная дважды дифференцируемой функции положительна
- 13. Схема исследования функции на выпуклость и точки перегиба: Найти вторую производную функции f′′(x). Найти точки, в
- 14. Пример. Найти интервалы выпуклости и точки перегиба графика функции y=x(x-1)3. Решение. 1. Найдем y′ =(x-1)2(4x-1), y′′
- 15. 6. Асимптоты графика функции Асимптотой графика функции y=f(x) называется прямая, обладающая тем свойством, что расстояние от
- 16. Теорема 2. Пусть функция y=f(x) определена при достаточно больших х и существует конечный предел функции Тогда
- 17. Пример. Найти асимптоты графика дробно-линейной функции Решение. Из области определения выпадает точка . Найдем пределы функции
- 18. 7. Общая схема исследования функций При исследовании функций и построении их графиков рекомендуется использовать следующую схему:
- 19. Пример. Исследовать функцию Решение. 1. Область определения функции: х≠±1. Точки пересечения с осью Ох находим из
- 20. Точка х=-1 является точкой разрыва второго рода. Возьмем х=1 Точка х=1 – точка устранимого разрыва. 4.
- 21. 5. Для нахождения экстремумов найдем первую производную функции: Здесь опять использовано разложение многочлена х3+х2+х-3 путем его
- 22. 6. Найдем точки перегиба, участки выпуклости вверх и вниз. Для этого вычислим вторую производную Ни при
- 23. Пример. Исследовать функцию 1. Функция определена при всех значениях х, для которых x2-1>0, т.е. на интервалах
- 24. В точке функция не определена. Следовательно, имеется только одна критическая точка принадлежащая области определения функции. Вся
- 26. Скачать презентацию




















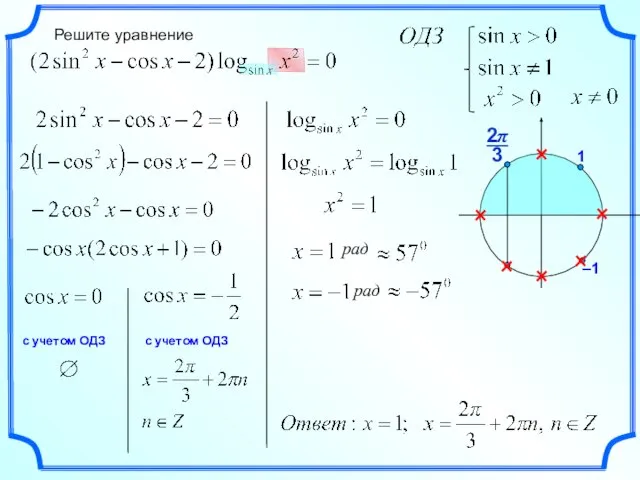 Решение уравнения
Решение уравнения Умножение 2 и на 2
Умножение 2 и на 2 Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Конус – тело вращения
Конус – тело вращения Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Свойства функции
Свойства функции Решение задач
Решение задач Равенство фигур
Равенство фигур Признаки подобия треугольника
Признаки подобия треугольника Цирк. Геометрические фигуры
Цирк. Геометрические фигуры Тест Вписанные и описанные цилиндры
Тест Вписанные и описанные цилиндры Понятие многогранника. Геометрические фигуры
Понятие многогранника. Геометрические фигуры Множества. Операции над множествами
Множества. Операции над множествами Определение и признаки параллелограмма
Определение и признаки параллелограмма Неопределенный интеграл
Неопределенный интеграл Презентация на тему Методы решения уравнений высших степеней
Презентация на тему Методы решения уравнений высших степеней  Математическая модель Память человека
Математическая модель Память человека Вычисление площадей и объемов. Лекция 5
Вычисление площадей и объемов. Лекция 5 Диаграммы
Диаграммы Функции и их свойства. Область определения и область значений функции
Функции и их свойства. Область определения и область значений функции Skreschivayuschiesya_pr
Skreschivayuschiesya_pr Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Методический материал по алгебре
Методический материал по алгебре Длина окружности
Длина окружности Прямая, луч, отрезок
Прямая, луч, отрезок Функция y = хх и её график
Функция y = хх и её график Решение задач по теме: Параллелограмм (1)
Решение задач по теме: Параллелограмм (1) Задачи на разрезания и перекраивания фигур
Задачи на разрезания и перекраивания фигур